[人工智能]python的神经网络入门（理论部分）

1、前言

本文只是我对神经网络的一些理解，且我希望能直白的描述神经网络的工作过程，所以文中很少使用较为晦涩的专业术语，大部分的都是大白话。如果文章有问题，欢迎批评指正。
注：文章是我看完《python神经网络编程》之后写的，所以大部分的图片都是书里的，并且思路也是跟着书走的，感兴趣的朋友可以去看看。

2、 初识神经网络

首先，在初学神经网络的时候，我们需要从最简单的机器入手，也就是所谓的预测机：
这里的计算就是预测的过程，可能你会不理解，“这里不是直接计算吗，有什么预测的功能”。实际上我们在预测时，是有一个训练集的，也就是把训练集当做一个正确答案，我们这里的计算就是使用训练集作为训练的样本，对数据进行训练，之后再对新给出的一个数据预测一个输出，如果还是不理解，就请先看看下面的例子 吧。
现在我们知道简单的预测机之后就开始构建一个简单的预测机，假设预测机的功能是千米转化为英尺（我们并不知道转换公式），那么输入就是千米，输出就是英里，我们的任务就是探索这里的“计算”的步骤：

现在我们知道输入和输出是一个线性的关系，那么我们可以假设输入为x，输出为y，则计算部分就是y=c*x（接下来请务必不要一下就看出c的值），那么这个时候就是训练集闪亮登场了，也就是这里的x和y的值的一个现实对应：

既然已经有了x和y的值，那么我们现在只需要猜测c的值就能完成预测，实际上，我们的训练就是针对c的调整。一般而言，我们都是先随机给出一个c值，然后对根据相关规则对c进行调整，那么这里给出c=0.5：

当我们使用c=0.5时，发现输出值和训练集上的100所对应的值（62.137）并不接近，这时可以得到误差，而误差也就是上面提到相关规则中最重要的指标。
误差值=真实值 - 预测值=62.137 - 50=12.137

那么现在就开始使用误差来调整c的值，也就是改变c使得误差变小，现使得c=0.6，然后观察误差的变化：
误差值=真实值 - 预测值=62.137 - 60=2.137

震惊！！误差竟然变小了，说明我们的方向是正确的，那我们还用刚刚的方法来减小误差，看看能不能使得误差小于现在的误差2.137，现在依旧增加c的值，使得c=0.7，让我们省略上面繁琐的步骤，我们可以得出 误差= -7.836，看来用力过猛了，那么接下来我们变换方法，慢慢微调，使得误差变小，当然这里的误差变小是和2.137比较，可以使用每次加0.1进行迭代，最终可以得到c的值。
好了！你已经学会了神经网络，接下来就去进行神经网络的编写吧！
哈哈，开玩笑的啦，下面是更精彩的部分。

3、分类器

其实学完上面的部分，你已经把神经网络的大致过程过了一遍了。那么现在来看看里面的细节吧。
因为上述的简单机器接受了一个输入，并做出应有的预测，输出结果，所以我们将其称为预测器，看到标题你应该也知道还有分类器，以下使用一个例子引入分类器：
我们在花园中看到各式各样的虫子，人眼一下子就可以区分毛毛虫和瓢虫，那么如何让电脑也可以识别昆虫的种类呢，现有一组训练集（还记得训练集的意义吧）在坐标轴上标出：

我想上面千米的案例已经掌握，那么沿用上面的思想，在此坐标轴上做一条直线，这条直线可以将毛毛虫和瓢虫给分开，也就是如果有一个需要预测的虫虫，如果他的坐标在该直线上方，则电脑就会认为此虫虫是毛毛虫，反之为瓢虫。我们想要的直线如下：

那么我们如何得到这条分界线呢？当然是和千米案例一样的思想了，既然要训练，那就必须要有训练集：

沿用千米转换思想，令直线的函数为y=ax，同样，已经知道x和y的值后，我们现在就要预测a的值，随机初始化一个数值，那么就令a=0.25，我们可以得到直线在坐标轴上的可视化表示：

这显然不是我们想要的结果，那么我们怎么判断是否是我们需要的分界线呢。我们不能看可视化的图像，而是应该利用数据。
我们来拿宽度为三的虫虫举例，当宽度为三时，我们想要的正确值是1，但是为1的话，直线就穿过了样本，这显然不能作为标准。作为分类器需要将两种昆虫分类，而不是预测。所以现在这里可以将正确的值改为1.1，也就是当宽度为3的时候，长度为1.1，这个样本就在正确样本之上，所以可以做分类样本。而此时预测的值为y=0.25*3=0.75 调整曲线还需要用到误差，那么就利用刚刚得到的数据来计算误差，E=误差=1.1-0.75=0.35

我们现在想要通过误差来调节a的值，所以我们必须要明确误差E和a的关系（接下来可能需要一点点数学基础了），我们知道y=a*x，现在定义我们期待的值为t（就是训练集中的1.1），现在为了得到t而去调整相应的a，我们总结千米转换的例子去微小的调节a，这就要用到数学中的Δ（高等数学中的微小的变化量），此时y=（a+Δa）x

这时新直线的斜率就是a+Δa，所以这里E=t-y=（a+Δa）x-ax=Δax，那么Δa=E/x
所以只需要拿之前得到的误差0.35除以3就可以得到即将要微调的Δa的值，Δa=0.1167，调节好斜率之后就可以得到a=0.3667。现在知道a的值之后，我们把毛毛虫的数据也代入函数中，y = 0.3667 * 1.0 = 0.3667，这和真实数据（3.0）差的有点远啊，说明我们必须还得继续调整，而鉴于之前的经验，我们可以将数据稍微调整，当宽度为1时，长度为2.9，根据上面的公式调整Δa，得到a=2.9，可是通过可视化数据发现我们训练的直线不能符合我们的要求：

通过图像我们可以看出，每次训练完，直线就会尽力去贴合最后一个训练数据，而不是做到分类的作用。
为了不让训练过猛，我们每次采用Δa=1/（我们实际上计算的Δa）。在机器学习中，这是一个重要的思路。我们应该进行适度改进（moderate）。也就是说，我们不要使改进过于激烈。我们采用ΔA 几分之一的一个变化值，而不是采用整个ΔA。所以引入一个参数L，这里的L称为学习率，就是为了每次稍微调节Δa的值，我们知道这里的L必须要小于1的。那么现在就给一个参数L=0.5。相应的，我们的公式变成了Δa=L（E/x）。
现在我们又要苦哈哈的从头计算，我们有一个初始值A = 0.25。使用第一个训练样
本，我们得到y = 0.25 * 3.0 = 0.75，期望值为1.1，得到了误差值0.35。ΔA = L（E / x ）= 0.5 * 0.35 / 3.0 = 0.0583。更新后的A值为0.25 + 0.0583 = 0.3083。
尝试使用新的A值计算训练样本，在x = 3.0时，得到y = 0.3083 * 3.0 =0.9250。现在，由于这个值小于1.1，因此这条直线落在了训练样本错误的 一边，但是，如果你将这视为后续的众多调整步骤的第一步，则这个结果不算太差。与初始直线相比，这条直线确实向正确方向移动了。
我们继续使用第二个训练数据实例，x = 1.0。使用A = 0.3083，我们得到y = 0.3083 * 1.0 = 0.3083。所需值为2.9，因此误差值是2.9-0.3083= 2.5917。ΔA = L(E / x ) = 0.5 * 2.5917 / 1.0 = 1.2958。当前，第二个更新的值 A等于0.3083 + 1.2958 = 1.6042。

这样得到的图像差不多就可以满足我们的要求了，一个分类器就诞生了！

4、 激活函数

学完上面，我们就进入了神经网络的学习了。为什么叫做神经网络呢？实际上，电脑中的神经网络就是为了模拟人类大脑的神经网络。还记得高中生物书上的神经图吗？

回忆一下吧，每次有突触小泡里的物质接触到突触后就会将信息传递。而我们学习的神经网络就是做的和它类似的工作–传递信息。而在这里有个关键的步骤就是激活函数，也就是物质刚刚接触突触后膜的时候。这里可以使用阶跃函数来模拟是否需要传递信息的开关。

假设阶跃函数的最大值为1，最小值为零，那么当输出为1时，说明该神经被激活，反之，则没有激活。这个函数的美中不足就是它太有棱有角了，所以我们需要该进，让曲线变得平滑：

这就是大名鼎鼎的sigmoid函数（阈值函数）了，那么现在来看看表达式吧：

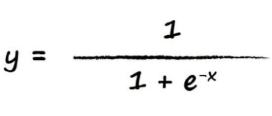
这个公式都是大佬们精推细算的，所以不要在意为什么要选取这个函数。既然知道了激活函数，我们就来看看单个神经元吧，来观察一下激活函数起到什么样的作用。
相必你还不知道，文章开头的那个千米转换其实就是单个神经元，也就是下面图片中的小圈圈:

单个神经元可以接受多个输入，然后在神经节点中计算之后，把计算出来的数据传递给激活函数，最后输出，神经元的内部结构如下图：

是不是觉得小小的神经元的功能还挺多的，只要把这些神经元组合在一起就能组成神经网络啦。注意，这里的总和输入值只是一个举例，并不是所有的神经元内部对输入数据都是这样处理的。下面来看一下整体的图：

那么根据这个现实中的神经图就可以绘制电脑中的神经网络图了，将上面的神经圆表示为上面的小圈圈，信号表示为数据，就可以得到下面的图：

数据从输入进入第一层，然后在神经元的内部进行计算和激活（内部结构上面讲过了哦），再分别将数据往下一层的各个神经元传递，直到输出。现在来详细的介绍一下计算过程：
第一层并不会对数据进行处理，只是做一个传递，比如从第一个输入箭头输入3，那么出第一层的数据就是3，如图所示：

如果第一层输出3，那么3就会往下一层传，往下一层传时，就需要引入权重这个参数了。也就是处理这个“3”时所需要的参数（下图中第一层的w₁₂意思是第一层的1指向第二层的2，其他权重也就一目了然了）。

你可能看到这里就会迷迷糊糊，怎么就要用到权重参数了呢？其实在第二层时，神经元内部结构就是正常的结构，会有计算函数和激活函数，我想你已经猜到了，对，这个权重参数就是计算函数中的参数，而且和之前的例子一样，权重参数是随机给出的（一般是-0.1~+0.1），后面会提及如何调整权重。第二层中的其中一个神经元内部结构如下：

是不是觉得很简单了，那么下面来看个例子巩固一下（看完图自己先计算一下，看看输出是啥）：

联想内部结构，先来计算第二层的第一个，首先数据来自第一层的1和第一层的2，需要用到的权重是w11和w21，那么层二中的第一个神经元中的计算函数就是：1.0w11+0.5w21=1.05，注意到这里还不是输出，可不要忘了还有激活函数，把刚刚计算的1.05传到sigmiod函数中激活神经元：y = 1 /（1 + 0.3499）=0.7408，同样算出第二个输出：

其实计算很简单，但是这只是最简单的一个神经网络的例子，我们平时要用的肯定不会这么简单，所以这时这样的计算就会显得繁琐并且麻烦，所以接下来我们需要使用数学工具–矩阵（永远的神）。

5、神经网络矩阵的使用

矩阵的性质以及计算方式我想大家必定比我都清楚，这里就不详细解释了（不会的需要补一补线性代数了哦）。那么怎么将神经网络和矩阵联系到一起呢？看看下面的图你就明白了：

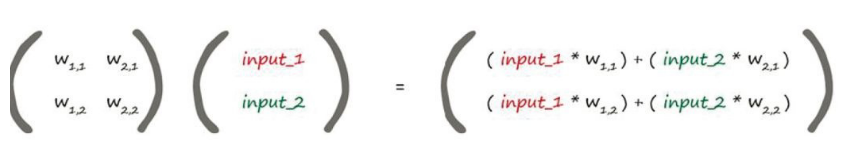
是不是惊讶的发现得出来的结果矩阵正是我们计算函数之后输出的值，计算规则一模一样。

现在输出就只差一个s（sigmoid函数，以后简称s函数）函数了，矩阵使用激活函数也很简单，只需要对矩阵中的每个元素进行处理就能输出啦，所以输出也是一个矩阵。这样就可以大大简化我们的步骤。
现在照例举一个例子加深理解：

既然使用矩阵的话就需要写出输入和权重矩阵（图中只标了部分权重参数），这里要说一下权重矩阵是如何写的：每个神经元需要的数据（数据来源线的权重）写成一行，所以第二层的第一个神经元的权重就是0.9 0.3…，整体写下来就是：

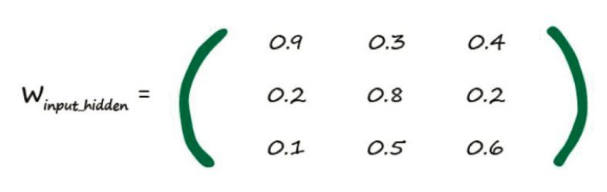
这下就好算了，只要将权重右乘输入矩阵就可以得到计算函数的输出了

依次类推，将x_hide进行s函数处理，最后最后就能得到输出啦！

6、权重的调节

做完上面这些，我们就可以来更新权重了。回忆一下最上面千米转换的案例，千米转换时，我们利用的是误差来更新，而现在我们也还是使用误差来更新权重。那么这里的误差是怎么计算的呢，其实对于这些数据来说，每个数据都有标签（相应的矩阵），也就是所谓的正确的标签，然后使用现在预测的矩阵减去正确的矩阵就可以得到误差矩阵。
但是你可能注意到了，对于一个输出神经元只有一个误差，而误差来源于上一层的不同神经元，所以现在就面临一个问题，每个来源对误差做出了多少影响？

一般来说，我们会使用权重来衡量每个来源带来了多少误差，对于w11来说，它对误差做出了3/（1+3）=3/4的贡献，同样，对于为w21，它带来了1/4的误差。

那么这里就可以看出误差分割的规则了：


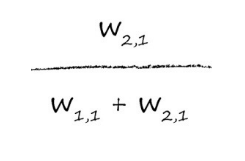
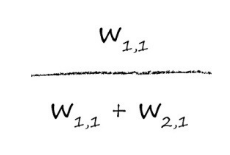
同样的，简单网络是这样计算，复杂的网络也是这样计算的：


像这样把误差往反方向传播就叫做误差的反向传播，而把数据向前传递就是正向传递，误差反向传播是神经网络中很重要的概念，后面还会介绍更加复杂的反向传播。

7、误差的反向传播

上面既然可以对数据的前向传播进行矩阵运算，那么同样误差的反向传播也可以使用矩阵，先来看一下如何构造前一层的误差：

但是这样写的话，这里的分数会太过麻烦，所以我们约定可以使用各自的权重来当矩阵（实际上述用分数（上图）和下图直接用权重的效果是一样的）。

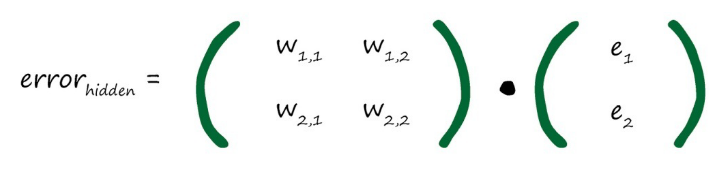
这样的话我们就构造出了误差的反向传播的矩阵，如果将前向传播的矩阵称为A，那么这里的矩阵该怎么用A表示呢？对了，就是A^T，如果将A进行转置就可以得到反向传播的权重矩阵了，所以E_前一层=A^T * E_最终误差。一切都变得合理了起来👏👏👏。
学会了这些，我们就来看看如何更新权重吧，更新权重的标准就是误差，而好的权重就是为了使得误差最小化，现在我们假设误差的图像如下图所示：

如果想要使得误差最小，就必须要到达最低点，而我们现在就是想得到最低点处x的坐标值，那么这里很容易就能联想到高等数学中的极值的求法，但是，在学高等数学的时候，我们就注意到一般函数不止一个极值点，其实在神经网络中，并没有那么准确的计算，就像是之前看到的毛毛虫和瓢虫的分类器，我们并没有那么准确的确定具体的分界线，而这里的误差极小值只需要足够小就可以了，并不需要最小。来看看三维热力图吧：

这里慢慢摸索到最低处，每次走的步子大小也由我们决定，也就是所谓的步长，步长太大的话，我们走的就会反复横跳，也就是之字形步伐：

导致最后可能得不到正确的结果。如果步长太小又会导致执行效率太慢。所以调整步长也很重要。这样看来我们需要调整的参数可真多。
作为调整各个参数标准的误差，我们要使它尽量的发挥作用，现在来直观的看看误差各种处理的差别：

由表可以知道，当误差进行平方处理的时候是最合理的，原因如下：
使用误差的平方，我们可以很容易使用代数计算出梯度下降的斜率。
误差函数平滑连续，这使得梯度下降法很好地发挥作用——没有间断，也没有突然的跳跃。
越接近最小值，梯度越小，这意味着，如果我们使用这个函数调节步 长，超调的风险就会变得较小。
既然一切准备就绪，我们就来看看怎么通过误差来调节权重吧。
现在我们以误差作为纵坐标，权重作为横坐标，以此来画图，那么我们可以轻松的得到误差图像某点的斜率：

这里使用斜率作为更新权重的方向，也就是说当斜率越来越小时，我们就即将到达低处。现在咱们来看一看神经网络图中的表示：

现在我们来计算o_k处的误差偏导数：

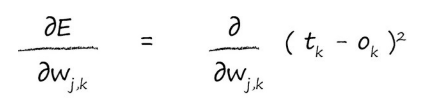
注意，这里之所以用t_k-o_k是因为对o_k做出贡献的只有w_jk。
这里的公式还是有些复杂，我们并不能使用所知的未知数来计算出偏差，那么接下来就来简化公式：
我们先用链式法则来把公式拆开，逐个击破：

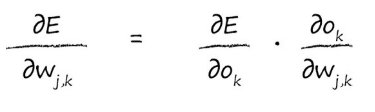
这里的$$\frac{?(E)}{?(O_k)}$$是误差E直接对输出O_k求偏导，这里的误差为（t_k-o_k）² 所以只需要用误差公式对o_k求导即可，代入可得(哈哈，这里的求导法则就不需要我说了吧)：

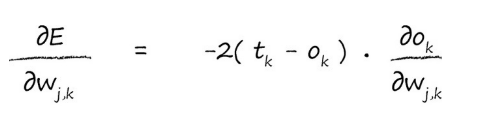
既然前面已经简化了，现在就剩下后面的部分了，后面部分·，可以从O_k入手，我们知道O_k的来源，也就是为O_k作出贡献的权重，即w_ik，那么我们只需要保持k不动，去遍历前一层所有和k相关的节点不就行了吗，假设前一层一共十个节点为O_k做出了贡献，那么i的取值范围就是1-10。我们将所有权重和上一层对应的输出作积后累加，再取s函数，就可以得到O_k，看看图能不能理解：

现在带入可得：

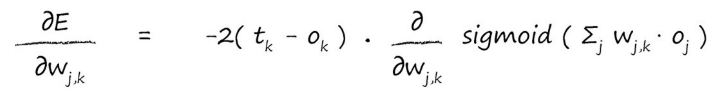
这里又遇到了一个难题，如何对s函数进行微分呢？别怕，有数学家已经算出微分函数了：

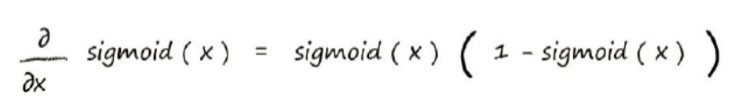
现在将x替换为∑_jw_jkO_j，这样就可以带入计算了：

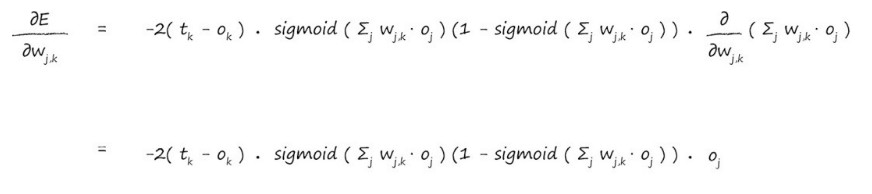
现在已经算出了梯度方向，我们把前面的常数给去掉问题就变的简单的多，之所以可以把常数给去掉，是因为我们只需要知道梯度的方向，并不关心其他的，那么现在函数就是：

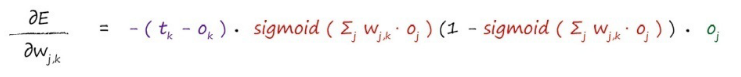
知道关键函数之后，我们可以得出新的权重：

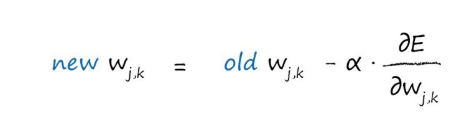
如果斜率为正，我们希望减小权重，如果斜 率为负，我们希望增加权重，因此，我们要对斜率取反（这里是减号而不是加号）。符号α是一个因 子，这个因子可以调节这些变化的强度，确保不会超调。我们通常称这个因子为学习率(他的作用和之前说过的L效果差不多)。
它的矩阵表示就是：

现在可以将s函数表示为上一层的输出，那么矩阵形式就是：

举个栗子吧：

现在已经知道了神经网络的误差以及权重，我们要更新这里的w₁₁=2.0，回忆权重更新公式：

1. 第一项（t_k -o_k ）得到误差e ₁ = 0.8。
2. S函数内的求和Σ_j w_j,k o_j =（2.0×0.4）+（3.0 * 0.5）= 2.3。 sigmoid 1/(1 +
   e ^-2.3 ) =0.909。
3. 中间的表达式为0.909 *（1-0.909）= 0.083。 由于我们感兴趣的是权重w_1,1
   ，其中j=1，也因此公式中最后一项o_j 也很简单，也就是输出层的前一层的输出。此处，o_j 值就是0.4。
4. 将这三项相乘，同时不要忘记表达式前的负号，最后我们得到-0.0265。 如果学习率为0.1，那么得出的改变量为- （0.1 *
   -0.02650）= +0.002650。
5. 因此，新的w1,1 就是原来的2.0加上0.00265等于2.00265。
   虽然这是一个相当小的变化量，但权重经过成百上千次的迭代，最终会确定下来，达到一种布局，这样训练有素的神经网络就会生成与训练样
   本中相同的输出。

8、总结

学到这里，神经网络的理论知识差不多就完了，当然这只是入门,后面可以看看卷积神经网络、残差神经网络、循环神经网络等等，以后的路还很长呐。这篇文章相当于是看完《python神经网络编程》之后做的笔记，然后自己进行了一点补充。如果朋友们想要了解，可以自己去看一遍.最后总结一下神经网络的流程吧！

后面会写使用python如何码代码，想看的话点个关注吧💕💕💕💕