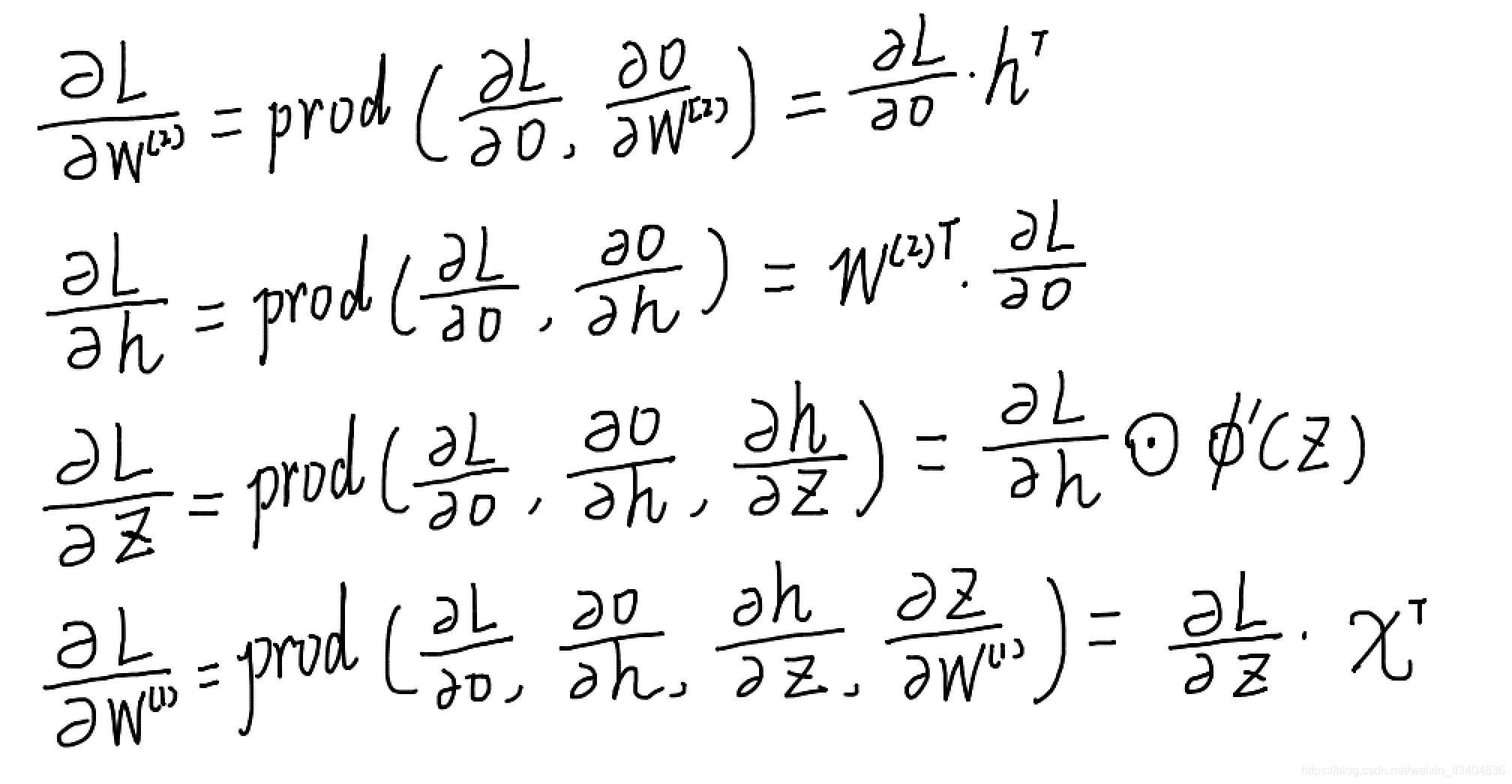开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 深度学习学习笔记（一） -> 正文阅读

[人工智能]深度学习学习笔记（一）

一、神经网络基础

1、几个词的包含关系

2、人工神经元

人工神经元： 人类神经元中抽象出来的数学模型。
M-P模型： 基于人工神经元提出下面的模型。
人工神经网络： 大量神经元以某种连接方式构成的机器学习模型。
例如：
感知机（Perceptron）： 只有输入和输出层；激活函数为阶跃函数。
- 缺陷： 无法解决异或问题，本质上是线性的，当然无法解决异或问题。

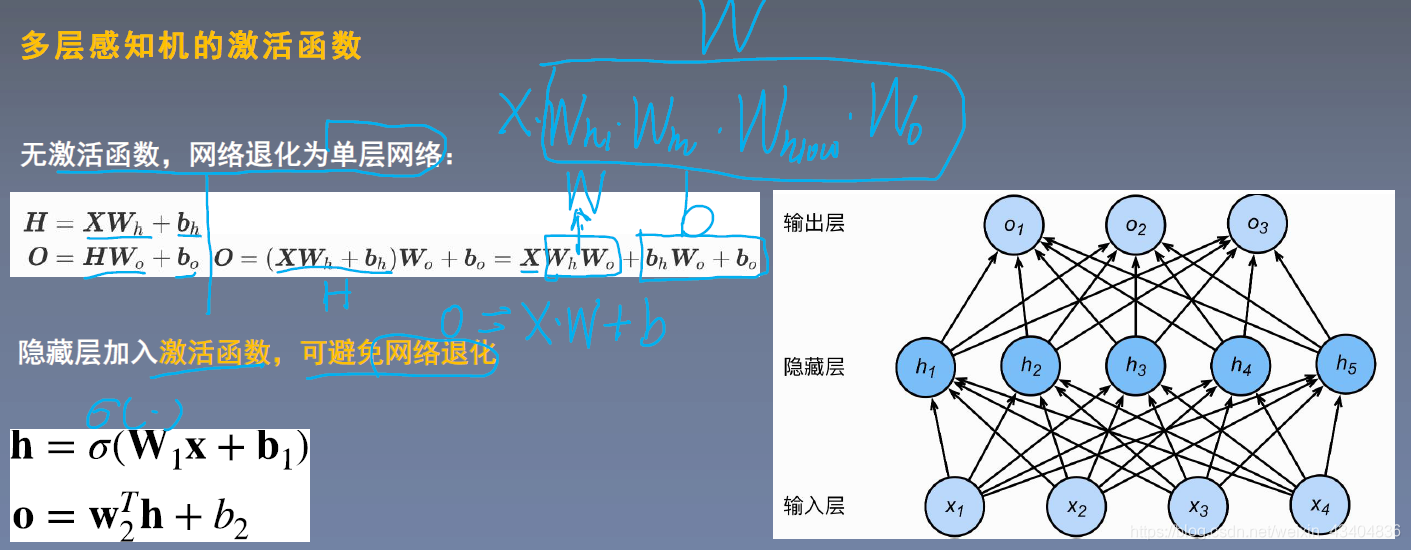
3、多层感知机

定义： 在单层神经网络基础上引入一个或多个隐藏层，使神经网络有多个隐藏层。
多层感知机的前向传播：
$Input:H=σ_1（Xw_1）$ $Output:O=σ_2(Hw_2)$
$σ ()$ 为激活函数。
为什么需要激活函数？

4、激活函数

激活函数的作用：
(1) 让多层感知机成为真正的多层，否则等价于一层
(2) 引入非线性，使网络可以逼近任意非线性函数 (万能逼近定理，ununiversal approximator)。
激活函数需要的性质：
(1) 连续并可导（允许少数点上不可导），便于利用数值优化的方法来学习网络参数。
(2) 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
(3) 激活函数的导函数的值域要在合适区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。
常见的激活函数：
- (1) Sigmoid函数（S型）：
  $g(x)=\frac{1}{1+e^{-x}}$ $g^{'}(x)=g(x)*(1-g(x))$
  
  特点： 简单，导函数两边存在饱和区（趋近于0），梯度几乎是零，会导致网络训练比较困难，导数中间部分趋近线性，称为线性区。
  值域：(0,1)
- (2) Tanh函数（双曲正切）：
  $tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ $g^{'}(x)=1-(g(x))^2$
  
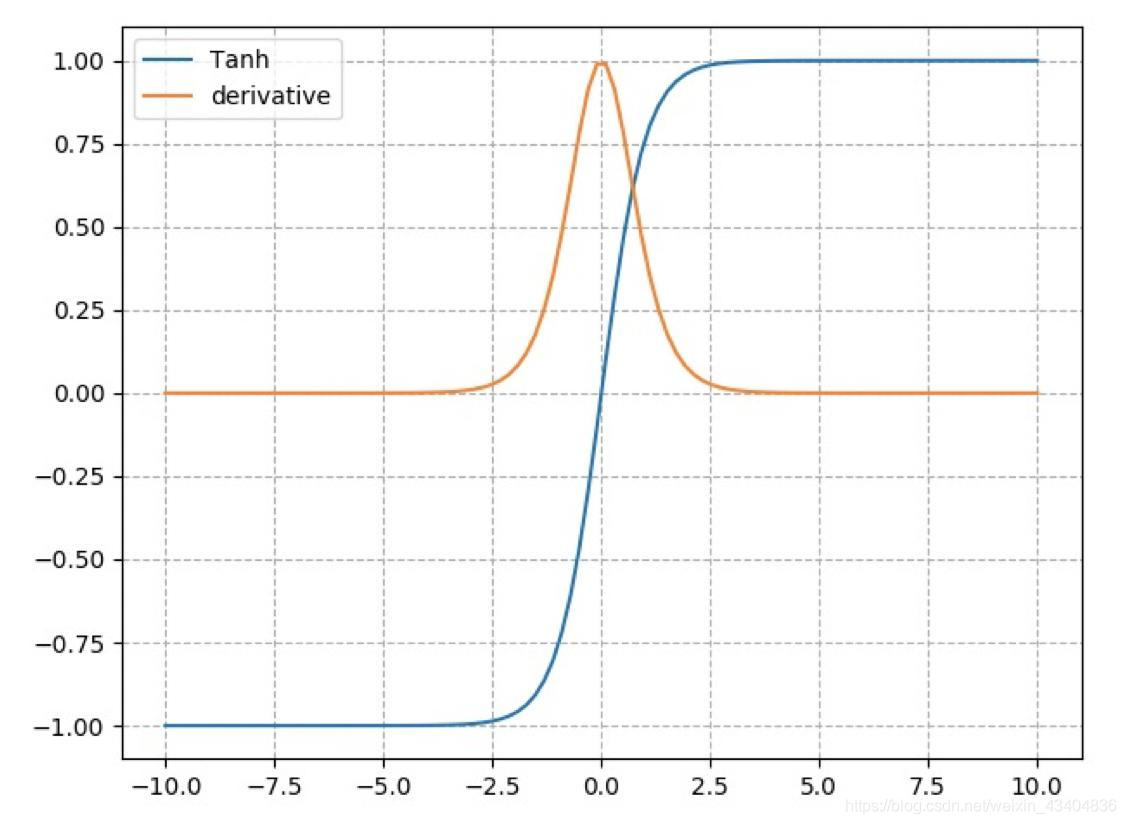
  特点： 对称，也同样存在饱和区和线性区。
  值域：(-1,1)
- (3) ReLu函数：
  $R e L u = m a x (0, x)$ $g^{'}(x)= \begin{cases} 1& \text{x>0}\\ undefined& \text{x=0}\\ 0& \text{x<0} \end{cases}$
  
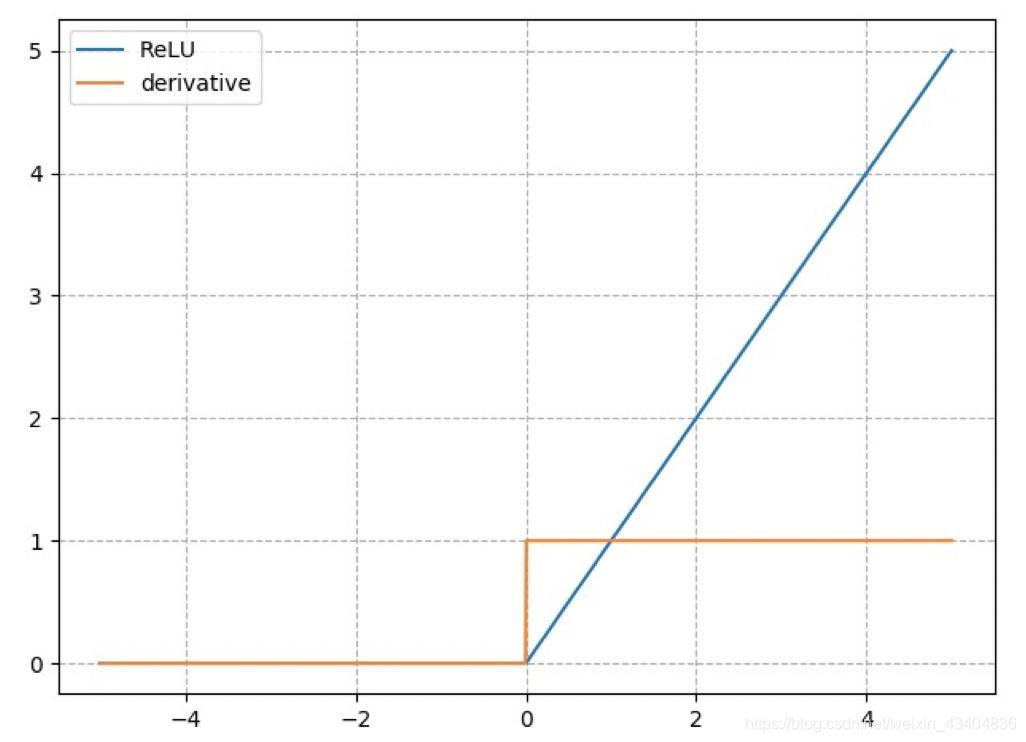
  特点： 主要运用在CNN隐藏层中，在0处不可导，可以人为设置为0或1。
  总结： 分为两类：前两个为饱和类型激活函数，ReLu为非饱和激活函数。

5、反向传播

前向传播： 输入层数据开始从前向后，数据逐步传递至输出层。
反向传播： 损失函数开始从后向前，梯度逐步传递到第一层。
反向传播作用： 用于权重更新，使网络输出更接近标签。
反向传播原理： 微积分中的链式求导法则： $y = f (u), u = g (x)$ $\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x}$
传播示意图：
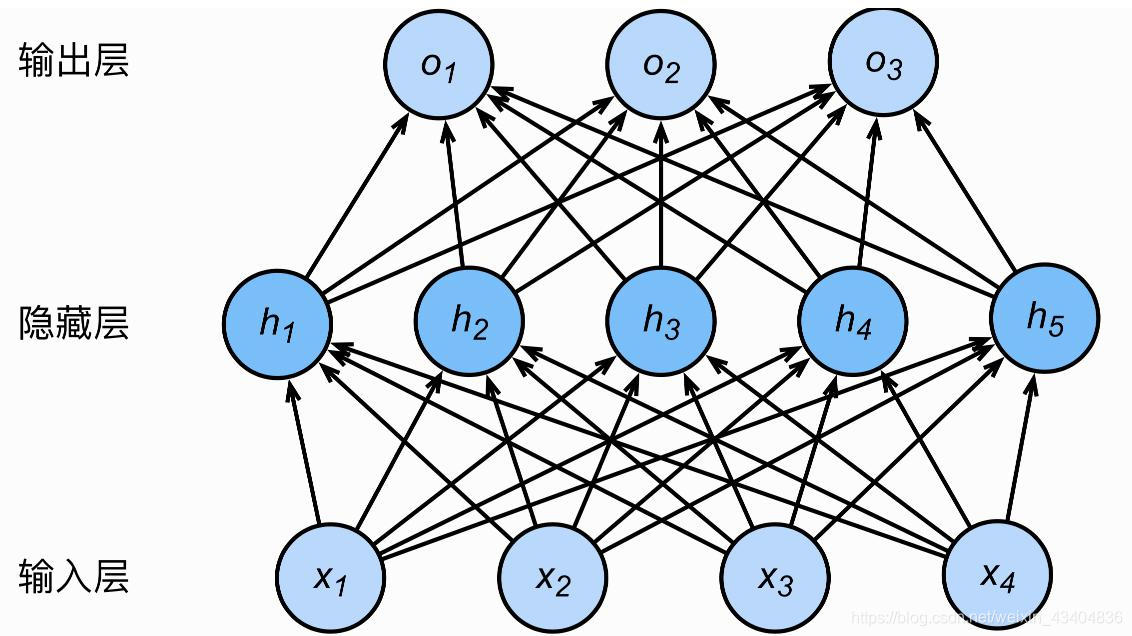
具体传播：

图片来源：https://d2l.ai

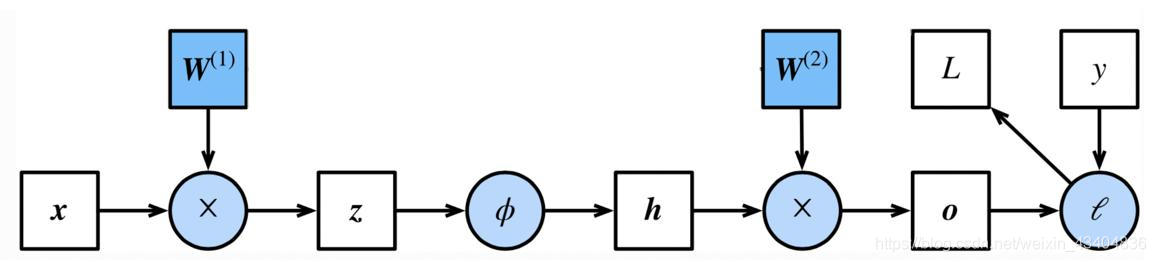
梯度下降法：
权值沿梯度负方向更新，使函数值减小。
导数： 函数在指定坐标轴上的变化率。
方向导数： 指定方向上的变化率（多元函数）。
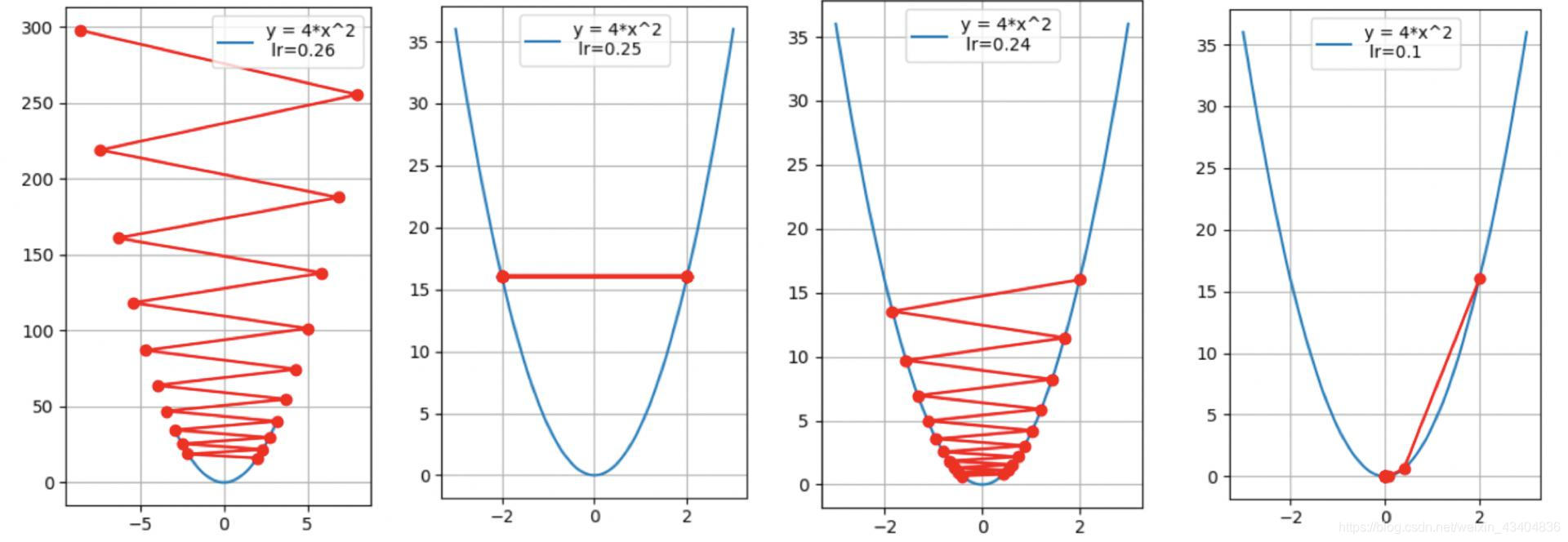
梯度： 一个向量，方向为方向导数取得最大值的方向
学习率： 控制更新步长。

6、损失函数

三个函数的区别：
- 损失函数： 衡量模型输出与真是标签的差异， $Loss f(y^,,y)$ （描述的是单样本）。
- 代价函数： $Cost=\frac{1}{N}\sum_i^Nf(y_i^,,y_i)$ （描述的是总体）。
- 目标函数： $O b j = C o s t + R e g u l a r i z a t i o n T e r m$ （加上了正则项，防止过拟合）。
常见的损失函数：
- MSE（均方误差）： $MSE=\frac{\sum_i^N(y_i^,-y_i^p)^2}{n}$ ，常用在回归任务中。
- CE（交叉熵）： $H(p,q)=-\sum_{i=1}^np(x_i)logq(x_i)$ ，源自信息论，用于衡量两个分布的差异，常用在分类任务中。
  $p$ 是真实分布， $q$ 是模型。
相关概念：
- 相对熵（又叫K-L散度） $D_{kl}(P||Q)$ 、交叉熵 $H (p, q)$ 、信息熵 $H (x)$
  $\begin{aligned} D_{K L}(P \| Q)=E_{x \sim p}\left[\log \frac{P(x)}{Q(x)}\right] &=E_{x \sim p}[\log P(x)-\log Q(x)] &=\sum_{i=1}^{N} \mathrm{P}\left(\mathrm{x}_{i}\right)\left(\log P\left(\mathrm{x}_{i}\right)-\log \mathrm{Q}\left(\mathrm{x}_{i}\right)\right) \end{aligned}$
  $H(p,q)=-\sum_{i=1}^np(x_i)logq(x_i)$
  $H(\mathrm{x})=E_{x \sim p}[I(x)]=-E[\log P(x)]=-\sum_{i=1}^{N} p_{i} \log \left(p_{i}\right)$
  三个之间关系： 交叉熵=信息熵+相对熵，即：
  $H(p,q)=H(p)+D_{kl}(P||Q)$
  因此优化交叉熵等价于优化相对熵。
注意点：
- 交叉熵：衡量两个概率分布的差异
- 概率有两个性质：
  1 . 概率值是非负的
  2 . 概率之和等于1
交叉熵的好伙伴——Softmax函数： 将数据变换到符合概率分布的形式。
$y_{i}=S(\boldsymbol{z})_{i}=\frac{e^{z_{i}}}{\sum_{j=1}^{C} e^{z_{j}}}, i=1, \ldots, C$
没有一个适合所有任务的损失函数，损失函数设计会涉及算法类型、求导是否容易、数据中异常值的分布等问题。
更多损失函数可到PyTorch网站：https://pytorch.org/docs/stable/nn.html#loss-functions
函数解读： https://zhuanlan.zhihu.com/p/61379965

7、权值初始化

定义： 训练前对权值参数赋值，良好的权值初始化有利于模型训练。
注意点： 全部初始化为零（错误做法，会使神经网络退化）（权重也不能太大，容易进入激活函数的饱和区）。
初始化方法：
- 随机初始化方法： 高斯分布随机初始化，从高斯分布中随机采样，对权值进行赋值，比如 $N (0, 0.01)$ 。
  - 自适应标准差： Xavier初始化、Kaiming初始化（MSRA）。

8、正则化方法

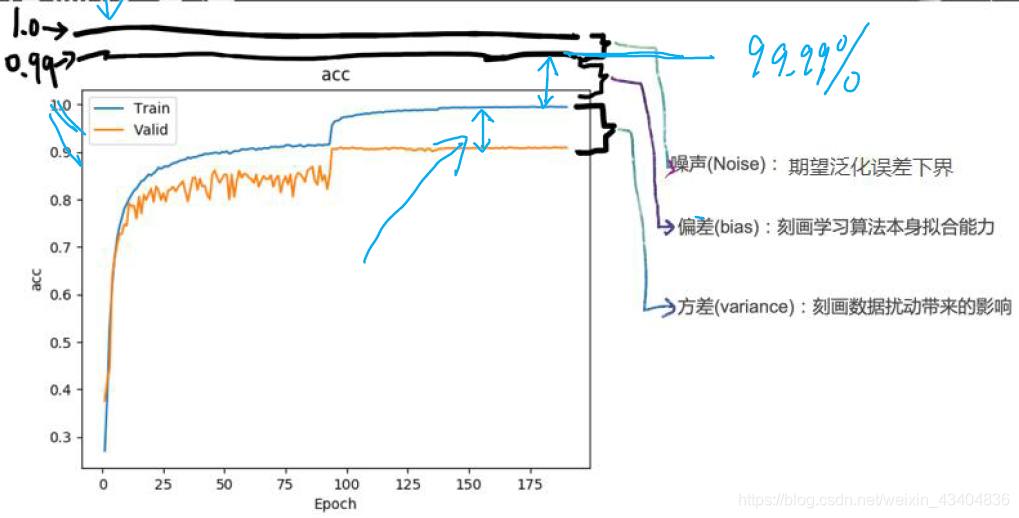
Regularization： 减小方差的策略，通俗理解为减轻过拟合的策略。
误差=偏差+方差+噪声
- 偏差： 度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
- 方差： 度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
- 噪声： 则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界。
过拟合： 方差过大，在训练集表现良好，在测试集表现糟糕。
正则化： L1正则 $w_i|$ 、L2正则（也叫权值衰减） $w_i^{2}$ ：
- 目标函数（加了L2正则）： $Obj=Loss+\frac{\lambda}{2} * \sum_{i}^{N} w_{i}^{2}$
- 无正则项： $w_{i+1}=w_{i}-\frac{\partial O b j}{\partial w_{i}}=w_{i}-\frac{\partial L o s s}{\partial w_{i}}$
- 有正则项： $\lambda∈(0,1)$
  $w_{i+1}=w_{i}-\frac{\partial O b j}{\partial w_{i}}=w_{i}-(\frac{\partial L o s s}{\partial w_{i}}+\lambda^{\star} w_{i} .)=w_{i}(1-\lambda)-\frac{\partial L_{i}}{\partial w_{i}}$
- 效果对比：

另一种正则化方法：
Dropout：随机失活
- 优点： 避免过度依赖某个神经元，实现减轻过拟合
- 随机： dropout probability （eg：p=0.5）
- 失活： weight = 0
- 注意事项： 训练和测试两个阶段的数据尺度变化测试时，神经元输出值需要乘以p。如图：

其他正则化方法：

回顾

在这里插入图片描述

二、卷积神经网络

1、卷积网络发展史

卷积神经网络（convolutional neural networks，CNN）： CNN是针对图像领域任务提出的神经网络，经历数代人的发展，在2012年之后大部分图像任务被CNN统治，例如图像分类，图像分割（图像分割就是把图像分成若干个特定的、具有独特性质的区域并提出感兴趣目标的技术和过程），目标检测（也叫目标提取，是一种基于目标几何和统计特征的图像分割），图像检索（文本+图像）等。

图像分割
目标检测
结构进化史：

2、卷积层

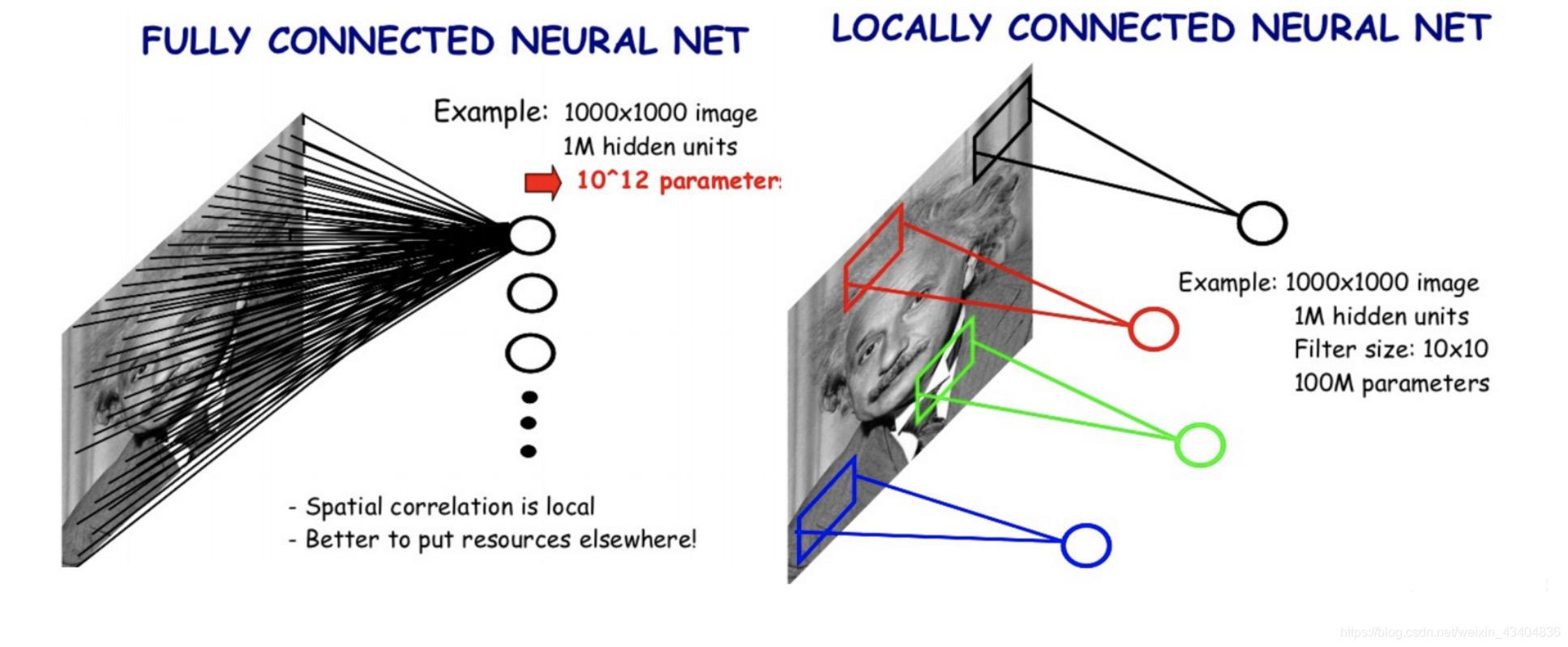
图像识别特点：
- 特征具有局部性： 老虎重要特征“王字”仅出现在头部区域。
- 特征可能出现在任何位置
- 下采样图像，不会改变图像目标
- 如图:

CNN由图像识别得到的启发：
- (1) 特征具有局部性：卷积核每次仅连接 $K ? K$ 区域， $K ? K$ 是卷积核尺寸：
(2) 特征可能出现在任何位置：卷积核参数重复使用（参数共享），在图像上滑动：

卷积核： 具可学习参数的算子，用于对输入图像进行特征提取，输出通常称为特征图（feature maps）：

卷积层操作：
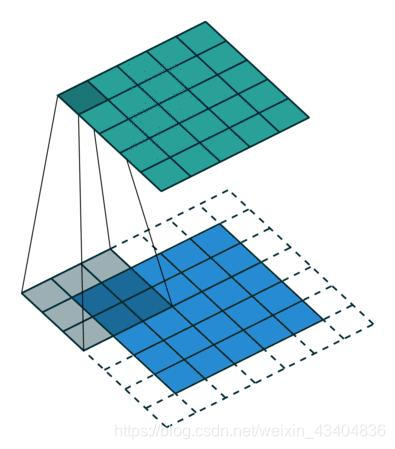
- Padding（填充）： 在输入图像的周围添加额外的行/列。
  - 作用：
  - 使卷积后图像分辨率不变，方便计算特征图尺寸的变化
  - 弥补边界信息“ 丢失”
- Strike（步幅）： 卷积核滑动的?数和列数称为步幅，控制输出特征图的大小，会被缩小1/s倍。
- 如何计算经过Padding和Strike后的输出图片大小？
  $\left.F_{o}=\mid \frac{F_{\text {in }}-k+2 p}{s}\right]+1$
  $F_o：输出大小$
  $F_in：输入大小$
  $k ： F i l t e r 的大小$
  $p ： P a d d i n g 大小$
  $s ： S t r i k e 大小$
- 多通道卷积： RGB图像是 $3 ? h ? w$ 的三维的数据，第一个维度3，表示channel，通道数。
  一个卷积核是3-D张量，第一个维与输入通道有关
  注：卷积核尺寸通常指高、宽

在这里插入图片描述

3、池化操作

启发于图像识别第三个特点： 下采样图像，不会改变图像目标：降低计算量，减少特征冗余。
池化： 一个像素表示一块区域的像素值，降低图像分辨率。
方法：
- Max pooling： 取最大值
- Average Pooling： 取平均值
输出尺寸计算与卷积操作类似
注意： 池化层无可学习参数

- **==池化作用==：** - 缓解卷积层对位置的**过度敏感**

对输入加入影响噪声变化，池化后影响减小：

减少冗余
降低图像分辨率，从而减少参数量

4、Lenet-5及CNN结构

网络结构：
- C1层： 卷积核 $K 1 = (6, 1, 5, 5), p = 1, s = 1 ， o u t p u t = (6, 28, 28)$
- S2层： 最大池化层，池化窗口 $= (2, 2) ， s = 2 ， o u t p u t = (6, 14, 14)$
- C3层： 卷积核 $K 3 = (16, 6, 5, 5), p = 1, s = 1 ， o u t p u t = (16, 10, 10)$
- S4层： 最大池化层，池化窗口 $= (2, 2) ， s = 2 ， o u t p u t = (16, 5, 5)$
- FC层： 3个FC层输出分类
注意： 前四层相当于是feature提取，FC层是根据特征进行分类层。
- 特征提取器： C1、S2、C3、S4
- 分类器： 3个FC层