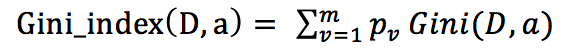Kmeans:
K-means算法,也称为K-平均或者K-均值,一般作为掌握聚类算法的第一个算法。
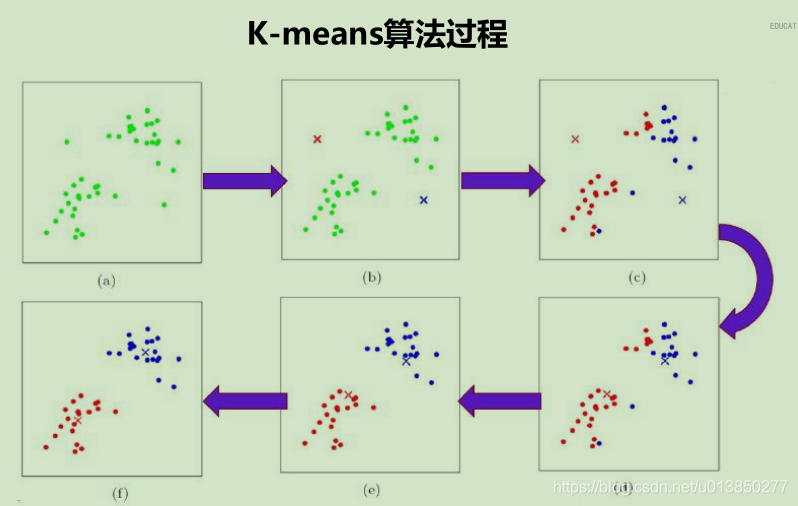
如上图以 K 为2,样本集为M 来描述KMean算法,算法执行步骤如下:
(1)随机选取K个点做为初始聚集的簇心(也可选择非样本点);
(2)分别计算每个样本点到 K个簇核心的距离(这里的距离一般取欧氏距离或余弦距离),找到离该点最近的簇核心,将它归属到对应的簇;
(3)所有点都归属到簇之后, M个点就分为了 K个簇。之后重新计算每个簇的重心(平均距离中心),将其定为新的“簇核心”;
(4)反复迭代 2 - 3 步骤,直到达到某个中止条件。
注:常用的中止条件有迭代次数、最小平方误差MSE、簇中心点变化率;
优点:
(1)理解容易,聚类效果不错;
(2)处理大数据集的时候,该算法可以保证较好的伸缩性和高效率;
(3)当簇近似高斯分布的时候,效果非常不错。
缺点:
(1)K值是用户给定的,在进行数据处理前,K值是未知的,给定合适的 k 值,需要先验知识,凭空估计很困难,或者可能导致效果很差。
(2)对初始簇中心点是敏感的。
(3)不适合发现非凸形状的簇或者大小差别较大的簇。
(4)特殊值(离群值或称为异常值)对模型的影响比较大。
为了解决K-Means算法对初始簇心比较敏感的问题,有许多衍生算法,例如:二分K-Means算法、K-Means++算法、Canopy算法。
KNN:
- 最简单且常用的分类算法之一
- KNN的原理就是当预测一个新的值x的时候,根据它距离最近的K个点是什么类别来判断x属于哪个类别。
- 有监督学习中的分类算法 (KNN是需要正确的样本数据进行学习的)
- 它看起来和另一个机器学习算法Kmeans有点像(Kmeans是无监督学习算法),但却是有本质区别的。KNN是对有标识的数据(labeled data)进行分类;Kmeans则是对无标识的数据进行分群。(我的理解)
优点:
(1)简单易用
(2)模型训练时间快
(3)预测效果好。
(4)对异常值不敏感
缺点:
(1)对内存要求较高,因为该算法存储了所有训练数据
(2)预测阶段可能很慢
(3)对不相关的功能和数据规模敏感
实例:
假如我有一套房子打算出租,但不知道市场价格,我就可以根据自己房子的规格(面积、房间数量、厕所数量、容纳人数等)(特征),在已有数据集中查找相似(K近邻)规格的房子价格,看别人的相同或相似户型租了多少钱。
已知的数据集中,每个已出租住房都有房间数量、厕所数量、容纳人数等字段,并有对应出租价格。
将我的房子数据与数据集中每条记录比较计算欧式距离,取出距离最小的5条记录,将其价格取平均值,可以将其看做我的规格房子的市场平均价格。
过程中有值得注意的点:
1、最好不要将所有数据全部拿来测试,需要分出训练集和测试集,我的习惯是75%训练&25%测试,具体划分比例按数据集确定;
2、理想情况下,数据集中每个字段取值范围都相同,但实际上这是几乎不可能的,如果计算时直接用原数数据计算,则会造成较大训练误差,所以需要对各列数据进行标准化或归一化操作,尽量减少不必要的训练误差;
3、数据集中非数值类型的字段需要转换
找女朋友(根据对方几个特征而预测到底适不适合做女朋友)
(1) 收集数据: 提供文本文件。
(2) 准备数据: 使用python解析文本文件。
(3) 分析数据: 使用matplotlib画二维扩散图。
(4) 训练算法: 此步驟不适用于K近邻算法。
(5) 测试算法: 使用部分数据作为测试样本。通常我们只提供已有数据的 90 %作为训练样本来训练分类器 ,而使用其余的 10% 数据去测试分类器。
(6) 使用 算 法: 产生简单的命令行程序,然后输入一些特征数据以判断对方是否为自己喜欢的类型。
朴素贝叶斯:
- 贝叶斯分类是一类分类算法的总称
- 朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。
- 贝叶斯公式(核心算法)


实例:
给定一组数据,包括特征(是否性格好、是否个子高、是否上进)以及类别(嫁/不嫁)
然后判断一个特征为(不帅,性格不好,身高矮,不上进)的男生,嫁还是不嫁?

这个等式成立的条件需要特征之间相互独立。由此而得,朴素贝叶斯算法有一个强大的假设:各个特征之间相互独立。
在数据量很大的时候,频率是等于概率的。因此使用一开始给的统计数据进行计算,便可得到结果。最终结果是:
p(不嫁|不帅、性格不好、身高矮、不上进)>p (嫁|不帅、性格不好、身高矮、不上进),所以我们根据朴素贝叶斯算法可以给这个女生答案,是不嫁。
优点:
(1) 算法逻辑简单,易于实现
(2)分类过程中时空开销小
缺点:
理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。
而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
决策树(ID3、C4.5、CART)
- 决策树算法借助于树的分支结构实现分类。树的内部结点表示对某个属性的判断,该结点的分支是对应的判断结果;叶子结点代表一个类标。
- 决策树算法有一个好处,那就是它可以产生人能直接理解的规则,这是贝叶斯、神经网络等算法没有的特性;决策树的准确率也比较高。
算法:根据训练数据记录D生成一棵决策树.
输入:数据记录D(包含类标的训练数据集)
属性列表(候选属性集,用于在内部结点中作判断的属性)
属性选择方法(选择最佳分类属性的方法)
输出:一棵决策树.
信息熵(一个系统越是有序,信息熵就越低)
对于有K个类别的分类问题来说,假定样本集合D中第 k 类样本所占的比例为pkpk(k=1,2,...,Kk=1,2,...,K),则样本集合D的信息熵定义为:
Ent(D)=?∑Kk=1 pk?log2pk
(1)信息增益法
ID3算法使用信息增益作为划分数据集的依据。用信息增益划分的具体做法是:计算每一类特征V对应的信息增益,然后挑选信息增益最小的特征进行划分。
信息增益 = 原始熵 - 条件熵(整个数据集的熵称为原始熵,数据集D根据某个特征划分之后的熵为条件熵)
公式如下:
Gain(D,a)=Ent(D)?∑Vv=1|Dv||D|![]() ?Ent(Dv)
?Ent(Dv)
其中v 为特征a的一个分类,pv?为 v分类占特征a总个数的比例,Dv?根据特征a 的v分类进行划分之后的数据集。
(2)增益率法
?ID3所采用的信息增益划分数据集是可能对数目较多的属性有偏好,C4.5 算法避免了这个问题,使用“增益率”来选择最优化分属性。
信息增益率公式:
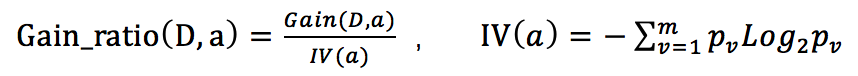
其中Gain_ratio(D,a) 表示 根据特征 a 划分之后的信息增益率, IV(a)为 特征a 的固有值
(3)基尼指数法
当CART用做分类树时,使用“基尼指数”来选择划分特征。基尼指数是另外一种表示数据集纯度的指标。与ID3、C4.5只能分类离散值相比,CART既可以作为离散型数据的分类决策树,也可以为连续型数据生成回归决策树。
基尼值:
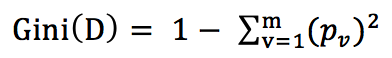
基尼指数: