卷积神经网络和传统网络的区别:
数据是三维矩阵
整体架构:
输入层
卷积层(提取特征)
池化层(压缩特征)
全连接层
即:卷积层负责提取图像中的局部特征;池化层用来大幅降低参数量级(降维);全连接层类似传统神经网络的部分,用来输出想要的结果。
卷积层
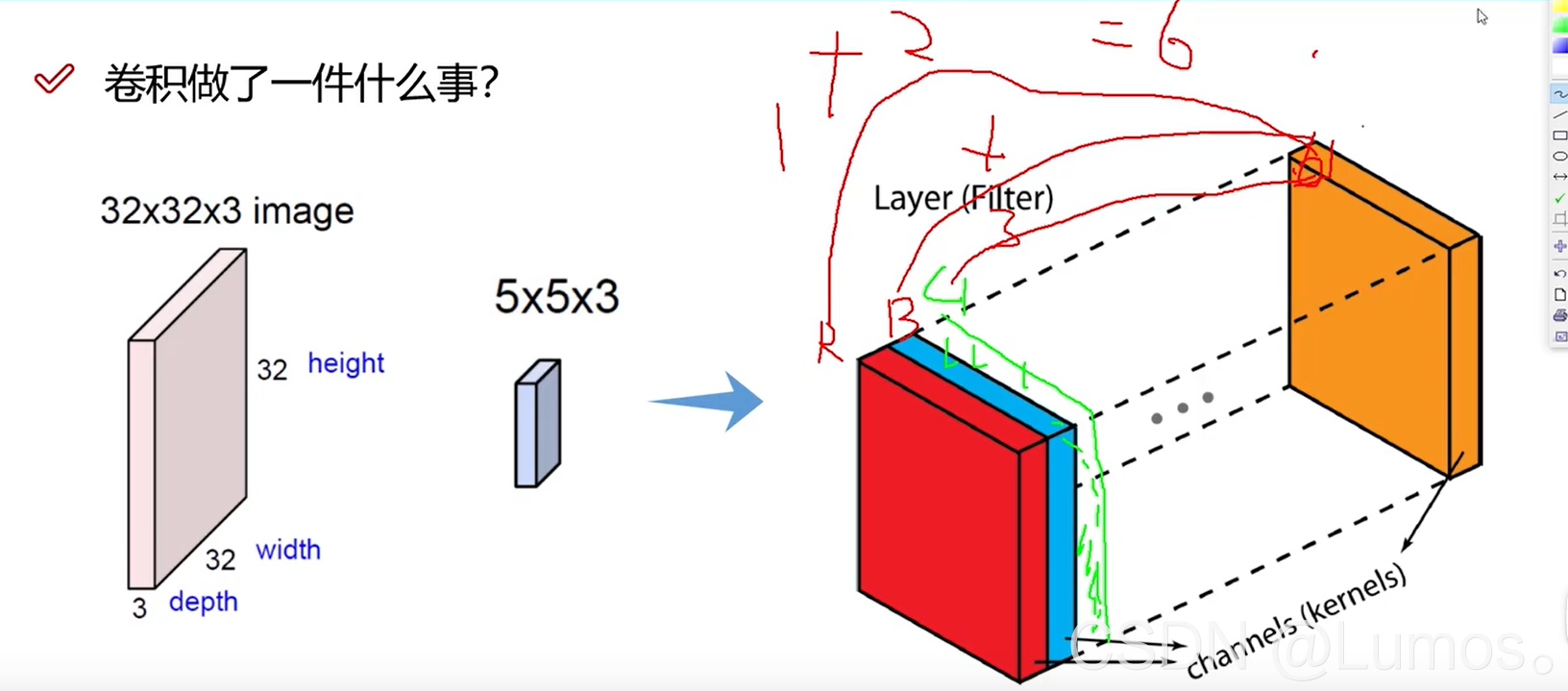
可以由RGB的概念作为理解:假设一个5x5x3的网络,由RGB三层堆叠在一起,R层为1,B层为2,G层为3。则最终得到结果为6。
(把三个通道的数据叠加在一起)
对每个区域来说,做特征提取,得到特征值。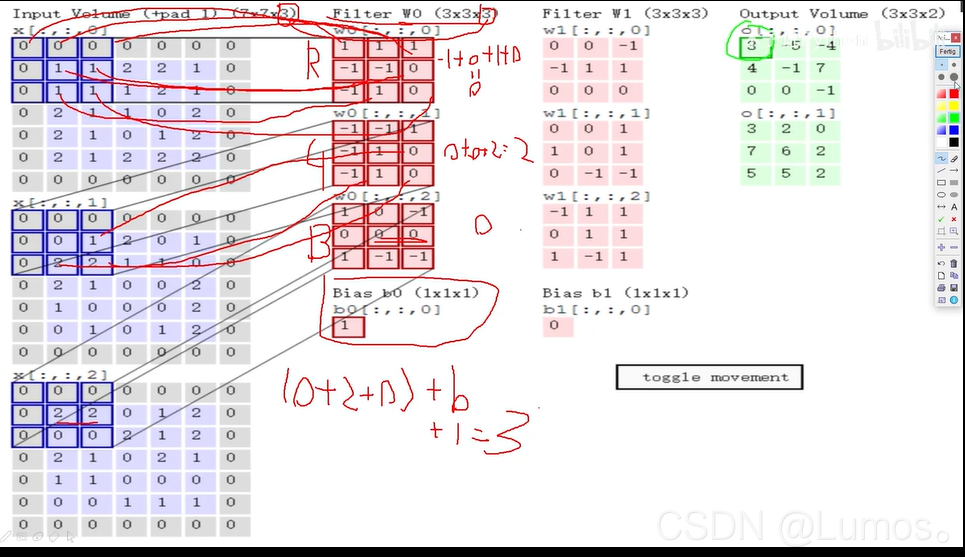
具体计算如上图:
(7x7x3:每层是7x7大小的,一共有三层)
Filter:卷积计算的权重。
Bias:相当于初始化每一层的特征值,在权重计算过后要加上初始化值,才能得到每层的特征值。
可以理解为使用一个卷积核来过滤图像的各个小区域,从而得到这些小区域的特征值。
特征图个数
特征图个数 = 卷积核个数
可以采用不同的卷积核,这样就会得到许多特征值,得到许多特征图,从而丰富特征值。
可以认为,每个卷积核代表了一种图像模式,如果某个图像块与此卷积核卷积出的值大,则认为此图像块十分接近于此卷积核。
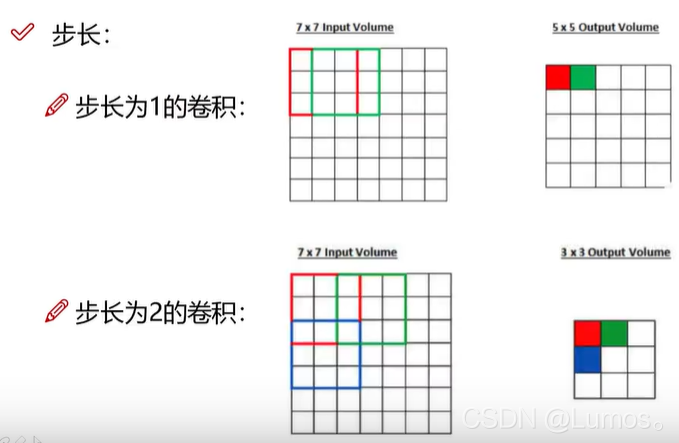
滑动窗口步长
步长太大,会导致有些数据不会重复计算,会有疏漏;
步长太小,有些数据重复计算数据大,重复区域面积大。
可以通过下图感知区别:
卷积核尺寸
卷积核越大看到的图片信息越多,因此获得的特征越好
普遍使用3x3的卷积核。
大的卷积核带来的参数量和计算量也会较大,小的卷积核是可以替代大的卷积核的,比如3个3x3卷积核来代替7x7卷积核,使用了2个3x3卷积核来代替5x5卷积核。
总的来说小卷积核的好处有:
- 减少计算量和参数量,加快模型训练;
- 可以添加更多卷积层,增强非线能力。
边缘填充
如果不使用边缘填充,会发生:输入图像与卷积核进行卷积后的结果中损失了部分值,输入图像的边缘被“修剪”掉了,这是因为边缘上的像素永远不会位于卷积核中心,而卷积核也没法扩展到边缘区域以外。
为解决这个问题,可以在进行卷积操作前,对原矩阵进行边界填充(Padding),也就是在矩阵的边界上填充一些值,以增加矩阵的大小,通常都用“0”来进行填充的。
池化层
作用:数据降维,避免过拟合。
之所以这么做的原因,是因为即使做完了卷积,图像仍然很大(因为卷积核比较小),所以为了降低数据维度,就进行下采样。
总结:池化层相比卷积层可以更有效的降低数据维度,这么做不但可以大大减少运算量,还可以有效的避免过拟合。
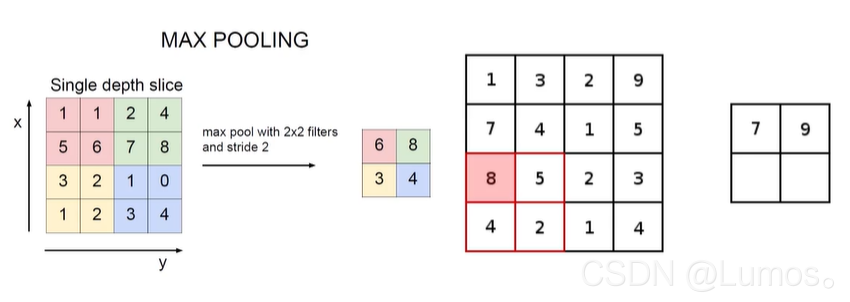
最大池化
选择最大池化的原因:特征值越大,表示越符合特征。
平均池化
在与最大池化的残酷战斗中惨烈败下阵来。因为容易被不符合的数据拉后腿…
全连接层
作用:输出结果
经过卷积层和池化层降维过的数据,全连接层才能”跑得动”,不然数据量太大,计算成本高,效率低下。
最后把矩阵转换为可以被全连接层计算的向量层。(贼拉长
计算
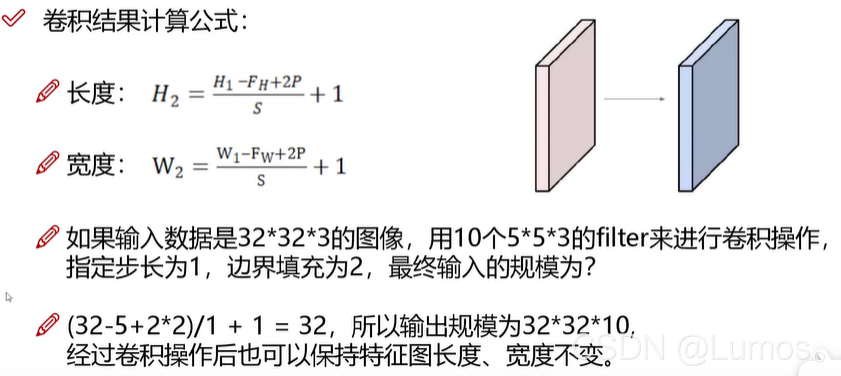
卷积结果计算公式
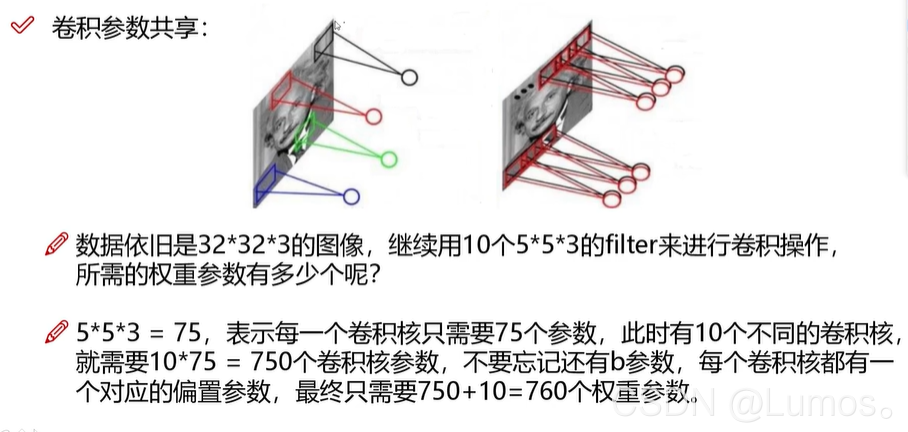
卷积参数共享
参考资料:
计算与理解:https://www.bilibili.com/video/BV1S64y1z7iX?p=68
卷积、填充、步长:https://zhuanlan.zhihu.com/p/77471866
代码学习:https://blog.csdn.net/weixin_43597287/article/details/97387801
https://zhuanlan.zhihu.com/p/112829371