[人工智能]论文阅读笔记《SuperGlue:Learning Feature Matching with Graph Neural Networks》

核心思想

??本文提出一种基于图神经网络的特征点匹配方法，把图像中的特征点看作图的节点，通过注意力机制聚合特征信息，得到用于匹配的特征向量。然后把匹配问题看作一个可微的最优运输问题（differentiable optimal transport problem），利用Sinkhorn Algorithm算法进行求解。整个算法的处理流程如下图所示

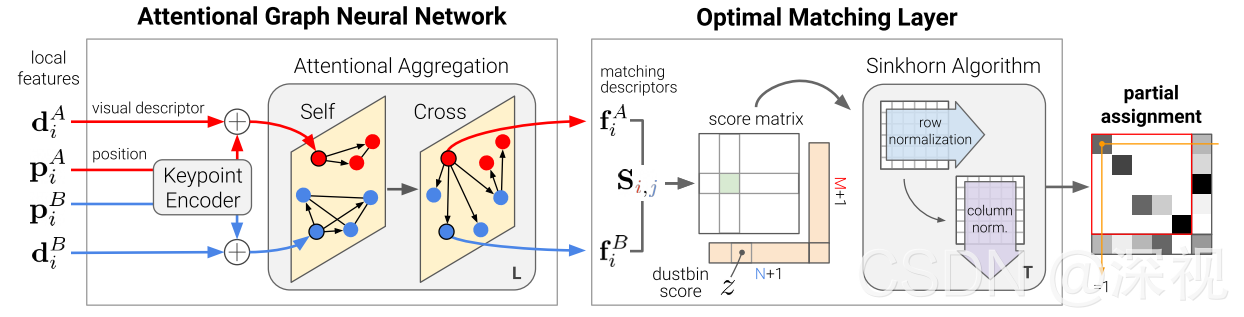
??首先，输入是两幅图像中特征点的位置坐标$p_i^A$和$p_i^B$，以及特征点对应的特征描述向量$d_i^A$和$d_i^B$。其中位置坐标$p_i^A$包含$x,y$坐标值以及检测置信度$c$，即$p_i=(x,y,c{)}_i$；特征描述向量$d_i^A$可以由任意的特征描述算子得到如SIFT或SuperPoint。位置坐标$p_i$经过一个由多层感知机构成的编码器处理后与特征描述向量$d_i$相加，得到图神经网络的一个节点$x_i$，该节点被称作局部特征

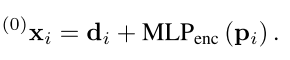
??为了获取上下文环境信息，本文采用图神经网络对特征信息进行聚合。本文提出一种多重图神经网络结构，将原图和待匹配图像中的特征点放在一起构成一个完整的图（graph），图中包含两种类型的无向边，一种是图像内部的边（Intra-image edges）也就是原图或待匹配图像内部特征点之间的连线，另一种是图像之间的边（Inter-image edges），即原图中的特征点和待匹配图像中的特征点之间的连线。因为包含两种类型的无向边，因此称为多重图神经网络。
??令${}^{(l)}{x}_i^A$表示第$l$层图神经网络中图像A中第$i$个特征点，则${}^{(l)}{x}_i^A$的更新方式如下

其中$[?||?]$表示级联操作，$m_{\epsilon \to i}$表示从特征点集向点$i$聚合的信息，$\epsilon$表示信息沿不同的边流动，如上文所述边的类型有两种， ε ∈ { ε s e l f , ε c r o s s } \varepsilon\in \{\varepsilon_{self}, \varepsilon_{cross}\} ε∈{εself?,εcross?}。对于奇数层，信息沿图像内部的边流动聚合，对于偶数层，信息沿图像之间的边流动聚合，采用交替的方式对每个节点进行更新。下面介绍聚合信息$m_{\epsilon \to i}$的计算方法，信息聚合的过程采用了注意力机制，对与待计算的特征点${}^{(l)}{x}_i^A$其聚合信息的计算过程如下

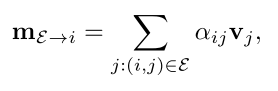
其中

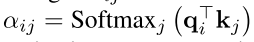
这个过程类似从数据库中检索数据，$q_i$表示查询向量，$k_j$表示键，而$v_j$表示每个键对应的值。对于本文而言$q_i$，$k_j$和$v_j$的计算过程如下

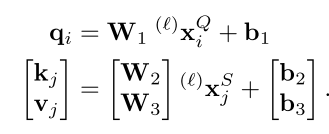
其中$x_i^Q$表示待计算的特征点，$x_j^S$就表示其他的用作信息来源的特征点。举个例子，假设当前处于奇数层，则用于信息汇聚的边属于图像内部的边，因此对于原图$A$中的特征点${}^{(l)}{x}_i^A$而言，他的聚合信息来源是原图$A$中除${}^{(l)}{x}_i^A$之外的其他所有特征点；而入党当前处于偶数层，则用于信息汇聚的边属于图像之间的边，因此对于原图$A$中的特征点${}^{(l)}{x}_i^A$而言，他的聚合信息来源是待匹配图像$B$中所有的特征点。上述公式中$W$和$b$都表示线性变换参数，对于每一层图神经网络中所有节点该参数是共享的，且可以通过学习获得。最终用于匹配的特征描述向量可表示为

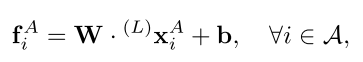
??得到用于匹配的特征描述向量后，通过两两之间进行内积计算可得到匹配得分矩阵$S\in R^{M\times N}$，$M,N$分别表示原图和待匹配图像中特征点的数量。

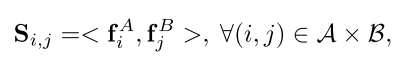
因为有些特征点受到遮挡问题的影响并不存在对应的匹配点，因此本文在得分矩阵的基础上增加一行和一列，表示垃圾箱。扩增后的得分矩阵$\bar{S}$，新添加的行和列得分为一个固定值$z$，这个值也可以通过训练得到。

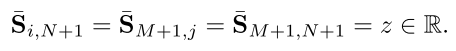
??$P\in R^{M\times N}$表示匹配矩阵，$\bar{P}\in R^{M+1\times N+1}$表示扩增后的匹配矩阵，其每一行都表示一个点与其他待匹配点之间的匹配概率，因为每个点至多存在一个匹配点，因此$\bar{P}$每一行的值加起来都为1。最后使用Sinkhorn Algorithm算法求解使得${\sum }_{i,j}{\bar{S}}_{i,j}{\bar{P}}_{i,j}$取得最大值的，最优匹配结果$\bar{P}$。

实现过程

网络结构

??所有的特征向量维度为256，图神经网络包含9层。

损失函数

??损失函数如下

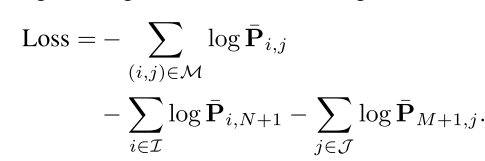
$M$表示匹配点集，$I,J$分别表示原图和待匹配图像中没有对应匹配点的点集

创新点

• 采用一种多重图神经网络结构用于汇集上下文信息
• 采用注意力机制计算汇集信息

算法评价

??本文使用图神经网络解决了特征点匹配问题，能够结合现有的特征描述算法，实现特征点的准确匹配。带有注意力机制的多层图神经网络能够有效的汇集上下文结构信息，使得匹配过程不仅关注特征点的局部特征，更能关注到整个图的全局信息。最后通过求解最优运输问题来实现点和点之间的最佳分配，取得了非常好的匹配效果。

如果大家对于深度学习与计算机视觉领域感兴趣，希望获得更多的知识分享与最新的论文解读，欢迎关注我的个人公众号“深视”。