Bi-Directional Center-Constrained Top-Ranking for Visible Thermal Person Re-Identification
BDTR: 双向中心约束的排序损失
1. 解决的问题
红外光和可见光图像之间差异大,而且存在大量的噪声,无法学习可判别的特征。而现有的方法对噪声图像具有弱鲁棒性。
多模态问题中出现模态间的特征映射关系不准确以及模态内变化巨大的问题。
2. 模型概览
- 提出双向中心聚合的排序损失函数同时考虑模态内和模态间的变化。
- 提出双向中心约束的排序损失将两个限制融合到一个公式里面,可以获得更好的性能。
小知识点:
- 浅层中的参数不同,用于建模特定于模态的信息,深层次的参数共享, 用于学习多模态共享特征。网络训练中引入双向双约束的top-ranking损失,并对其进行L2归一化处理。同时结合identity loss稳定训练过程,从而提高性能。
总结:
具体是引入了中心的概念,将不同模态的负样本对之间的度量从二范数精确到距离样本中心类的最小距离。不仅可以减小计算量,而且还可以减小模态之间的差异。
采用了anchor中心对中心计算loss 代替 anchor对anchor计算loss,因为所有anchor中心能够很好的代表着一类,只在中心计算ranking loss。
3. 模型详述
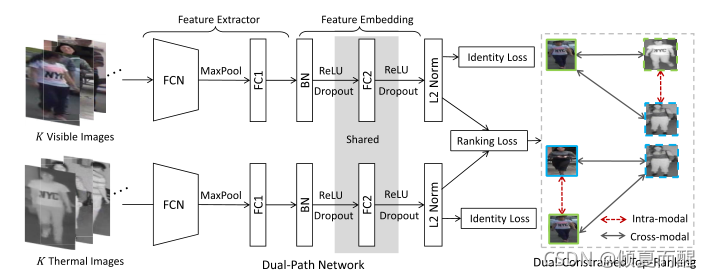
双流网络的特征学习和双向双约束的top-ranking损失的度量学习。
双路径网络的参数部分共享,以建模多模态的共享信息,独立参数挖掘模态特定信息。双约束的top-ranking损失学习低维度的特征嵌入,能够区分不同身份的两种异质模式。
浅层参数自定义,深层参数共享。
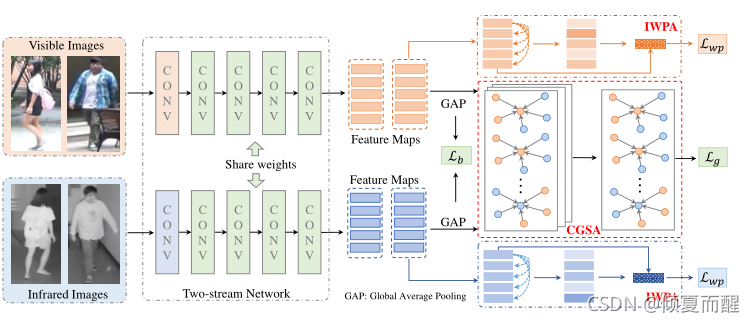
3.1 双流的网络
现成的特征提取器:都是为了捕获和提取人物图像的特征表示而设计的。然而,两条路径的网络参数被分别优化以捕获特定于模态的信息。由于VT-REID任务的训练数据有限,采用在大规模图像网络上预训练的通用图像分类网络参数初始化特征提取程序。
对于可见光和红外光的路径,使用AlexNet作为主干网络,浅卷积层通常捕获两种模式共享的低级视觉模式。在预先训练好的FC层之后添加一个BN层,如果不进行BN层,所有人物图像的特征将被压缩到特征空间的一个小区域中。从经验上看,BN操作显著提高了人员重新识别的性能。
特征嵌入:
目的是在两个异构模式之间学习一个有区别的低维嵌入空间,在双流网络之后引入共享的全连接层,这个共享结构提高了跨模态人员重识别的性能,充当投影函数将两种模式的特征投影到公共的嵌入空间。具体如下表示:
x
=
F
v
(
I
v
)
,
z
=
F
t
(
I
t
)
x = \mathcal F_v(I_v) , z = \mathcal F_t(I_t)
x=Fv?(Iv?),z=Ft?(It?)
3.2 双向双约束的排序损失
Ranking loss:
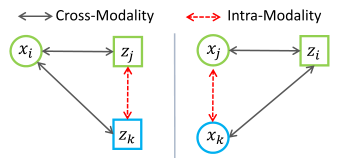
三个输入: x i , z j , z k x_i,z_j,z_k xi?,zj?,zk?, z i , x j , x k z_i,x_j,x_k zi?,xj?,xk?表示双向的跨模态三元组损失的输入.
x,z表示不同模态 颜色表示相同标签。则其距离应该满足:
D
(
x
i
,
z
j
)
<
D
(
x
i
,
z
k
)
?
ρ
1
,
??
?
y
i
≠
y
k
,
?
y
i
=
y
j
D
(
x
i
,
z
j
)
=
1
2
∥
x
i
?
z
j
∥
2
2
D(x_i,z_j) \lt D(x_i,z_k) - \rho_1, ~~ \forall y_i \neq y_k, \forall y_i = y_j \\ D(x_i,z_j) = \frac 1 2 \| x_i - z_j \|^2_2
D(xi?,zj?)<D(xi?,zk?)?ρ1?,???yi??=yk?,?yi?=yj?D(xi?,zj?)=21?∥xi??zj?∥22?
那么跨模态的行人重识别损失函数应该是:
L
b
i
=
∑
?
y
i
=
y
j
,
?
y
i
≠
y
k
max
?
[
ρ
1
+
D
(
x
i
,
z
j
)
?
D
(
x
i
,
z
k
)
,
0
]
+
∑
?
y
i
=
y
j
,
?
y
i
≠
y
k
max
?
[
ρ
1
+
D
(
x
i
,
z
j
)
?
D
(
x
i
,
z
k
)
,
0
]
\mathcal L_{bi} = \sum_{\forall y_i = y_j, \forall y_i \neq y_k} \max [\rho_1 + D(x_i, z_j)-D(x_i,z_k), 0] + \\ \sum_{\forall y_i = y_j, \forall y_i \neq y_k} \max [\rho_1 + D(x_i, z_j)-D(x_i,z_k), 0]
Lbi?=?yi?=yj?,?yi??=yk?∑?max[ρ1?+D(xi?,zj?)?D(xi?,zk?),0]+?yi?=yj?,?yi??=yk?∑?max[ρ1?+D(xi?,zj?)?D(xi?,zk?),0]
跨模态的排序损失
L
c
r
o
s
s
=
∑
?
y
i
=
y
j
max
?
[
ρ
1
+
D
(
x
i
,
z
j
)
?
min
?
?
y
i
≠
y
k
D
(
x
i
,
z
k
)
,
0
]
+
∑
?
y
i
=
y
j
max
?
[
ρ
1
+
D
(
z
i
,
x
j
)
?
min
?
?
y
i
≠
y
k
D
(
z
i
,
x
k
)
,
0
]
\mathcal L_{cross} = \sum_{\forall y_i = y_j} \max [\rho_1 + D(x_i,z_j)-\min_{\forall y_i \neq y_k} D(x_i,z_k),0] + \\ \sum_{\forall y_i = y_j} \max [\rho_1 + D(z_i,x_j)-\min_{\forall y_i \neq y_k} D(z_i,x_k),0]
Lcross?=?yi?=yj?∑?max[ρ1?+D(xi?,zj?)??yi??=yk?min?D(xi?,zk?),0]+?yi?=yj?∑?max[ρ1?+D(zi?,xj?)??yi??=yk?min?D(zi?,xk?),0]
双向跨模态的top-ranking loss有两个优点:
- 减少了交叉模态的变化同时保证了hard mining的高可分辨性,不需要off-line hard triplet sampling,所有的三元组比较都是在training batch的online进行;
- 双向训练策略确保学习的特征表示是模态不变的,提高了不同查询的鲁棒性。
模态内的排序损失
L
i
n
t
r
a
=
∑
max
?
[
ρ
2
?
min
?
?
y
i
≠
y
K
D
(
z
j
,
z
k
)
,
0
]
+
∑
max
?
[
ρ
2
?
min
?
?
y
i
≠
y
K
D
(
x
j
,
x
k
)
,
0
]
\mathcal L_{intra} = \sum \max[\rho_2 - \min_{\forall y_i \neq y_K} D(z_j, z_k), 0] + \sum \max[\rho_2 - \min_{\forall y_i \neq y_K} D(x_j, x_k), 0]
Lintra?=∑max[ρ2???yi??=yK?min?D(zj?,zk?),0]+∑max[ρ2???yi??=yK?min?D(xj?,xk?),0]
其中
ρ
2
\rho_2
ρ2?是一个预设定的值。
特征损失
由于不正确的关系度量,ranking loss可能会陷入收敛问题。同时,学习到的特征表示不能简单地利用关系信息来解决类内变化。此时引入identity损失:
L
=
λ
1
L
c
o
r
s
s
+
λ
1
L
i
n
t
r
a
+
λ
2
L
i
d
\mathcal {L = \lambda_1 L_{corss} + \lambda_1 L_{intra} + \lambda_2 L_{id}}
L=λ1?Lcorss?+λ1?Lintra?+λ2?Lid?
3.3 提出双向中心约束的排序损失
首先是中心的概念:
L
c
e
n
t
e
r
=
1
2
∑
i
=
1
K
D
(
x
i
,
c
y
i
)
\mathcal L_{center} = \frac 1 2 \sum^K_{i=1} D(x_i,c_{y_i})
Lcenter?=21?i=1∑K?D(xi?,cyi??)
c
y
i
∈
R
d
c_{y_i} \in \mathcal R^d
cyi??∈Rd是该类的中心。对跨模态的行人重识别问题而言,假设在每一个模态中,所有的标签都属于一个中心的子元素。这样就可以定义出双向中心损失:
L
b
i
c
e
n
t
e
r
=
∑
i
=
1
K
max
?
[
ρ
1
+
D
(
x
i
,
c
y
i
)
?
min
?
?
y
i
≠
y
k
D
(
x
i
,
c
y
k
)
,
0
]
+
∑
i
=
1
K
max
?
[
ρ
1
+
D
(
z
i
,
c
y
i
)
?
min
?
?
y
i
≠
y
k
D
(
z
i
,
c
y
k
)
,
0
]
\mathcal L_{bicenter} = \sum^K_{i=1} \max [\rho_1 + D(x_i,c_{y_i})-\min_{\forall y_i \neq y_k}D(x_i, c_{y_k}), 0] + \\ \sum^K_{i=1} \max [\rho_1 + D(z_i,c_{y_i})-\min_{\forall y_i \neq y_k}D(z_i, c_{y_k}), 0]
Lbicenter?=i=1∑K?max[ρ1?+D(xi?,cyi??)??yi??=yk?min?D(xi?,cyk??),0]+i=1∑K?max[ρ1?+D(zi?,cyi??)??yi??=yk?min?D(zi?,cyk??),0]
将anchor与sample的比较替换为anchor与center的比较的优点:减少计算量,原来模态内约束和跨模态约束共计4k^ 2,后来只需要计算样本和中心之间的样本对距离2k^2。
保留了处理跨模态的模态内变化的属性:三元组与中心的比较 确保不同形态的人身份上是可区分的;中心本身就限制了来自同一特征两种模态连接起来的采样,也解决了模态内的变化。
反向传播的分析
为了计算当前步骤中两种异质模式及其对应中心的输入特征表示的反向传播梯度,首先简化中心约束排序损失的表示,最小样本到类间中心距离
min
?
?
y
i
≠
y
k
D
(
x
i
,
c
y
k
)
,
min
?
?
y
i
≠
y
k
D
(
z
i
,
c
y
k
)
\min_{\forall y_i \neq y_k} D(x_i,c_{y_k}),\min_{\forall y_i \neq y_k} D(z_i,c_{y_k})
min?yi??=yk??D(xi?,cyk??),min?yi??=yk??D(zi?,cyk??)用
D
(
x
i
,
c
p
i
)
,
D
(
z
i
,
c
q
i
)
D(x_i,c_{p_i}),D(z_i,c_{q_i})
D(xi?,cpi??),D(zi?,cqi??)表示,那么
x
i
,
z
i
x_i,z_i
xi?,zi?的中心排序损失可以表示为:
L
 ̄
x
i
=
max
?
[
ρ
1
+
D
(
x
i
,
c
y
i
)
?
D
(
x
i
,
c
p
i
)
,
0
]
,
L
 ̄
z
i
=
max
?
[
ρ
1
+
D
(
z
i
,
c
y
i
)
?
D
(
z
i
,
c
p
i
)
,
0
]
\mathcal{\overline L_{x_i}} = \max [\rho_1 + D(x_i,c_{y_i})-D(x_i,c_{p_i}), 0] ,\\ \mathcal{\overline L_{z_i}} = \max [\rho_1 + D(z_i,c_{y_i})-D(z_i,c_{p_i}), 0]
Lxi??=max[ρ1?+D(xi?,cyi??)?D(xi?,cpi??),0],Lzi??=max[ρ1?+D(zi?,cyi??)?D(zi?,cpi??),0]
对下标的梯度可以表示为:
?
L
b
i
c
e
n
t
e
r
?
x
i
=
(
?
D
(
x
i
,
c
y
i
)
?
x
i
?
?
D
(
x
i
,
c
p
i
)
?
x
i
)
δ
(
L
 ̄
x
i
>
0
)
=
(
c
p
i
?
c
y
i
)
δ
(
L
 ̄
x
i
>
0
)
?
L
b
i
c
e
n
t
e
r
?
z
i
=
(
?
D
(
z
i
,
c
y
i
)
?
z
i
?
?
D
(
x
i
,
c
q
i
)
?
z
i
)
δ
(
L
 ̄
z
i
>
0
)
=
(
c
q
i
?
c
y
i
)
δ
(
L
 ̄
z
i
>
0
)
\frac {\partial \mathcal L_{bicenter}} {\partial x_i} = (\frac {\partial D(x_i,c_{y_i})} {\partial x_i} - \frac {\partial D(x_i,c_{p_i})} {\partial x_i})\delta(\mathcal{\overline L_{x_i}} \gt 0)\\ =(c_{p_i} - c_{y_i})\delta(\mathcal{\overline L_{x_i}} \gt 0)\\ \frac {\partial \mathcal L_{bicenter}} {\partial z_i} = (\frac {\partial D(z_i,c_{y_i})} {\partial z_i} - \frac {\partial D(x_i,c_{q_i})} {\partial z_i})\delta(\mathcal{\overline L_{z_i}} \gt 0)\\ =(c_{q_i} - c_{y_i})\delta(\mathcal{\overline L_{z_i}} \gt 0)\\
?xi??Lbicenter??=(?xi??D(xi?,cyi??)???xi??D(xi?,cpi??)?)δ(Lxi??>0)=(cpi???cyi??)δ(Lxi??>0)?zi??Lbicenter??=(?zi??D(zi?,cyi??)???zi??D(xi?,cqi??)?)δ(Lzi??>0)=(cqi???cyi??)δ(Lzi??>0)
同时对
c
j
c_j
cj?的梯度可以表示为:
?
L
b
i
c
e
n
t
e
r
?
c
j
=
∑
i
=
1
K
(
x
i
?
c
j
)
δ
(
L
 ̄
x
i
>
0
)
δ
(
y
i
=
j
)
1
+
∑
i
=
1
K
δ
(
L
 ̄
z
i
>
0
)
δ
(
y
i
=
j
)
?
∑
i
=
1
K
(
x
i
?
c
j
)
δ
(
L
 ̄
x
i
>
0
)
δ
(
p
i
=
j
)
1
+
∑
i
=
1
K
δ
(
L
 ̄
x
i
>
0
)
δ
(
p
i
=
j
)
+
∑
i
=
1
K
(
z
i
?
c
j
)
δ
(
L
 ̄
z
i
>
0
)
δ
(
y
i
=
j
)
1
+
∑
i
=
1
K
δ
(
L
 ̄
z
i
>
0
)
δ
(
y
i
=
j
)
?
∑
i
=
1
K
(
z
i
?
c
j
)
δ
(
L
 ̄
z
i
>
0
)
δ
(
q
i
=
j
)
1
+
∑
i
=
1
K
δ
(
L
 ̄
z
i
>
0
)
δ
(
q
i
=
j
)
\frac {\partial \mathcal L_{bicenter}} {\partial c_j} = \frac {\sum^K_{i=1}(x_i - c_j)\delta(\mathcal{\overline L_{x_i}} \gt 0)\delta(y_i = j)} {1 + \sum^K_{i=1}\delta(\mathcal{\overline L_{z_i}} \gt 0)\delta(y_i = j)} \\ - \frac {\sum^K_{i=1}(x_i - c_j)\delta(\mathcal{\overline L_{x_i}} \gt 0)\delta(p_i = j)} {1 + \sum^K_{i=1}\delta(\mathcal{\overline L_{x_i}} \gt 0)\delta(p_i = j)}\\ + \frac {\sum^K_{i=1}(z_i - c_j)\delta(\mathcal{\overline L_{z_i}} \gt 0)\delta(y_i = j)} {1 + \sum^K_{i=1}\delta(\mathcal{\overline L_{z_i}} \gt 0)\delta(y_i = j)} \\ - \frac {\sum^K_{i=1}(z_i - c_j)\delta(\mathcal{\overline L_{z_i}} \gt 0)\delta(q_i = j)} {1 + \sum^K_{i=1}\delta(\mathcal{\overline L_{z_i}} \gt 0)\delta(q_i = j)}
?cj??Lbicenter??=1+∑i=1K?δ(Lzi??>0)δ(yi?=j)∑i=1K?(xi??cj?)δ(Lxi??>0)δ(yi?=j)??1+∑i=1K?δ(Lxi??>0)δ(pi?=j)∑i=1K?(xi??cj?)δ(Lxi??>0)δ(pi?=j)?+1+∑i=1K?δ(Lzi??>0)δ(yi?=j)∑i=1K?(zi??cj?)δ(Lzi??>0)δ(yi?=j)??1+∑i=1K?δ(Lzi??>0)δ(qi?=j)∑i=1K?(zi??cj?)δ(Lzi??>0)δ(qi?=j)?
K表示一个训练batch中包含的图片数量。
此处使用SGD作为优化器
c
j
t
+
1
=
c
j
t
?
α
Δ
c
j
t
c^{t+1}_j = c^t_j - \alpha \Delta c^t_j
cjt+1?=cjt??αΔcjt?
最后的损失函数可以表示为:
L
=
λ
1
L
b
i
c
e
n
t
e
r
+
λ
2
L
i
d
\mathcal L = \mathcal {\lambda_1 L_{bicenter} + \lambda_2 L_{id}}
L=λ1?Lbicenter?+λ2?Lid?
采样策略的说明:

4. 实验结果
4.1 消融研究
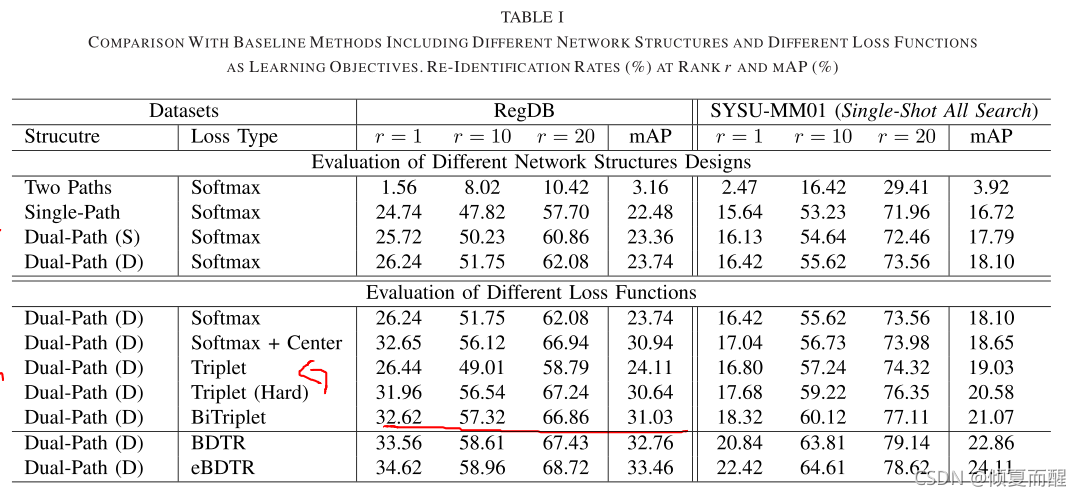
实现的具体细节:dropout rate=0.5, 在RGB数据集上 λ 1 = 1 , λ 2 = 0.1 \lambda_1 = 1, \lambda_2 = 0.1 λ1?=1,λ2?=0.1,在SYSU-MM01数据集上: λ 1 = 0.1 , λ 2 = 1 \lambda_1 = 0.1, \lambda_2 = 1 λ1?=0.1,λ2?=1所有配置可以在论文中看到。
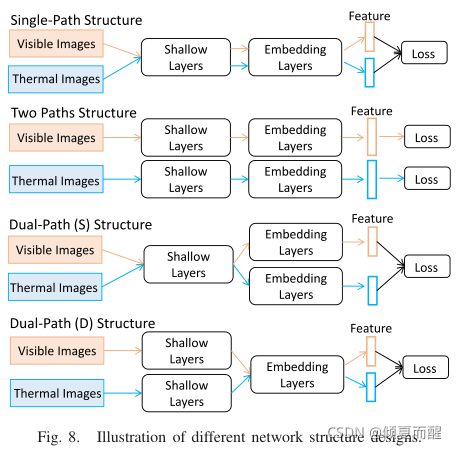
不同的网络结构对模型性能的影响。
表中第二大块是关于不同的损失函数对模型的影响。
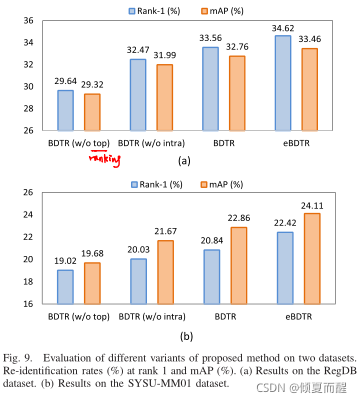
然后对于每一个模块作者进行了对比,结果如下:
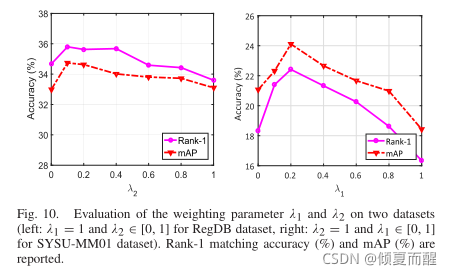
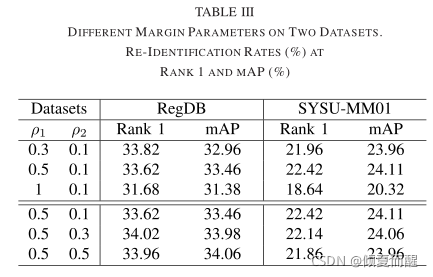
最后是不同的实验参数对结果的影响:
intergrating identity loss可以持续提高跨模态ReID的性能。大样本情况id loss可以获得很好的性能,小样本情况下,ranking loss可以获得很好的性能。
而直接从预先训练的ImageNet模型得到的ranking loss很难收敛,需要使用带有idloss的预训练参数进行初始化,进一步说明idloss对跨模态Reid的重要性。
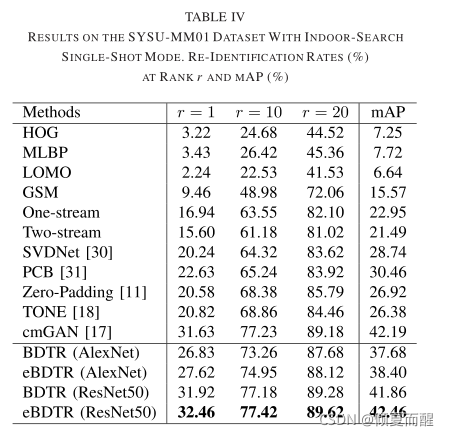
优点:无需任何人工干预的端到端学习可以获得有区别性的特征;提出的方法对跨模态的问题提供了一个很好的解决方案,同时eBDTR保留了处理两种模态变化的特性;集成的idloss有助于通过对特定身份信息建模稳定训练过程,还提高了ranking loss特征表示的可分辨性。
人类很难通过简单实用颜色信息判断哪个人是查询的正确匹配者。但是在夜间监控中起到重要作用。
即使排名列表中存在一些错误检索的示例,但由于纹理或结构信息相似,排名靠前的图像通常与查询图像非常接近。
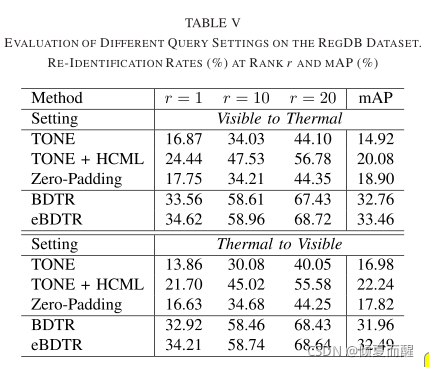
双向关系训练策略的有效性,增强了特征学习的模态不变性。
4.2 与SOTA方法比较
下表是与SOTA方法比较
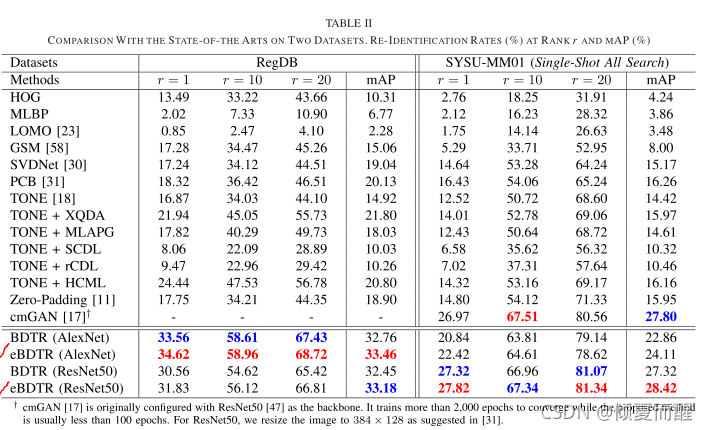
解决模态内变化的模态内约束将持续改进特征学习.
扩展的eBETR保留了同时处理跨模态和模态内变化的特性但约束较少。