Abstract
在MIMO系统中,利用发射机可用的信道状态信息(CSI)进行预编码对于提高频分双工(FDD)网络的性能至关重要。在MIMO系统中,在CSI feedback transmission中压缩大量信道状态信息是一个主要挑战。本文中我们提出使用RNN来学习时间相关性,并采用深度可分离卷积来收缩模型。特征提取模块也是通过研究不同结构中解耦的时空特征表示精心设计的。结果表明,该方法在恢复质量和准确性方面优于现有方法,并且在低压缩比下具有显著的鲁棒性。
1 Introduction
基于RecCsiNet结构,我们保留特征压缩和解压缩模块的结构,并通过在空间和时间域应用RNN和分离特征提取进一步改进了特征提取。借鉴MobileNet,使用深度可分离卷积来构建轻量级深度神经网络,主要贡献有:
- 在FDD MIMO系统中,提出了一种新颖而有效的CSI感知和恢复机制,称为ConvlstmDsiNet,它分别在特征提取、压缩和解压模块中利用了RNN的记忆特征。此外在特征恢复中采用深度可分离卷积来减少模型的大小和通道间的信息交互
- 我们通过探索在空间和时间域中解耦卷积的时空特征表示,进一步完善了特征提取模块中的ConvlstmCsiNet。实验结果表明,与现有的基于DL的模型相比,改进的ConvlstmCsiNet在不同压缩比下获得了最高的恢复质量。
2 CSI feedback system
FDD MIMO downlink system中,基站有 N t N_t Nt?个发射天线,每个用户设备有一个接收天线。有 N c N_c Nc?个子载波的正交频分复用中工作。第 n n n个子载波可以表示为:
y n = h ^ n H v n x n + z n y_n = \hat h^H_n v_nx_n + z_n yn?=h^nH?vn?xn?+zn?
其中 h ^ n ∈ C N t \hat h_n \in C^{N_t} h^n?∈CNt?表示瞬时信道向量、 v n ∈ C N t v_n \in C^{N_t} vn?∈CNt?表示预编码向量, x n ∈ C x_n \in C xn?∈C表示调制发射符号, z n ∈ C z_n\in C zn?∈C表示第 n n n个子载波处的附加噪声,那么CSI矩阵,表示为:
H ^ = [ h ^ 1 , h ^ 2 , . . . , h ^ N ^ c ] ∈ C N ^ t × N ^ c \hat H =[\hat h_1, \hat h_2, ... ,\hat h_{\hat N_c}] \in C^{\hat N_t \times \hat N_c} H^=[h^1?,h^2?,...,h^N^c??]∈CN^t?×N^c?
假设每个用户设备可以获得信道响应估计 H ^ \hat H H^ ,然后反馈给基站,以帮助基站生成预编码向量 v n v_n vn?。
从用户端到基站端的CSI反馈,实际需要涉及CSI压缩。
- H ^ \hat H H^ 在angular-delay domain中是稀疏的,在经历2D理算傅里叶变换(DFT)操作之后。
- 在延迟域,除了几个非零列之外, H ^ \hat H H^中的大多数元素都是零,因为直线路径周围的多径到达之间的时间延迟位于小的有限时间段内。因此第一个 N C N_C NC?非零列被保留,其余被去除,新的 N t × N c N_t \times N_c Nt?×Nc? CSI矩阵表示为 H H H
H H H保持不变,对于给定OFDM符号及其相关联的预编码向量,然而状态空间模型不断的发生变化,表示为 H t = [ h 1 , t , h 2 , t , . . . , h N c , t ] ∈ C N T × N c H_t = [h_{1,t}, h_{2,t}, ... ,h_{N_c, t}] \in C^{N_T\times N_c} Ht?=[h1,t?,h2,t?,...,hNc?,t?]∈CNT?×Nc?,是第 t t h t^{th} tth时间步长的瞬时CSI,同时下一个时间step可以表示为
H t + 1 = F ? H t + G ? u t H_{t+1} = F\cdot H_t+G\cdot u_t Ht+1?=F?Ht?+G?ut?
u t ∈ C N t × N c u_t \in C^{N_t\times N_c} ut?∈CNt?×Nc? 是加性噪声,元素 u t ( i , j ) ~ N ( 0 , σ u 2 ) u^{(i,j)}_t \sim N(0, \sigma ^2_u) ut(i,j)?~N(0,σu2?); F , G ∈ C N t × N t F,G \in C^{N_t\times N_t} F,G∈CNt?×Nt?属于权重矩阵,参数 α \alpha α表示相邻CSI矩阵之间的相关性。 F = ( 1 ? α 2 ) I F =(1-\alpha ^2)I F=(1?α2)I ; G = α 2 I G=\alpha ^2 I G=α2I ,所以时变信道的矩阵序列被定义为:$ {H_t } ^T_{t=1} ={H_1, H_2, …, H_T }$
传输过程中, { H t } t = 1 T \{H_t\}^T_{t=1} {Ht?}t=1T? 被分成实部和虚部,以降低复杂度,其中矩阵中的所有元素都被转换为实数并归一化到[0, 1]区间。在DFT和截断操作下,反馈参数的数量从 N ^ = 2 × N ^ c × N t \hat N = 2\times \hat N_c \times N_t N^=2×N^c?×Nt? 减到 N = 2 × N c × N t N=2\times N_c \times N_t N=2×Nc?×Nt? 。模型由用户端的编码器和基站端的解码器组成,编码器将大小为 N N N的信道状态信息(CSI)矩阵压缩到 M M M维度( M < N M<N M<N)的码字 s t s_t st?,解码器将压缩后的码字转换回原始信道状态信息矩阵。压缩率为 γ = M N \gamma=\frac M N γ=NM?。基站端完成恢复,得到 H t H_t Ht?,再通过补零列和执行反向DFT来输出最终矩阵 H ^ t \hat H_t H^t?
3 Proposed ConvlstmCsiNet with P3D Blocks
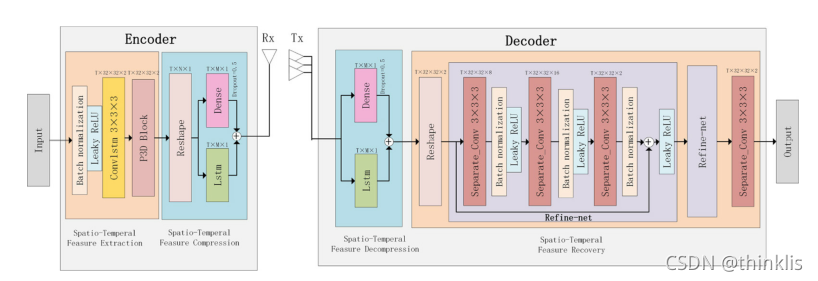
包括用户设备上的编码器和基站上的解码器。编码器分为两个模块,即特征提取和特征压缩;解码器由特征解压缩和特征恢复模块,其中再特征恢复模块中使用了RefineNet单元。
输入形状 T × 32 × 32 × 2 ( H = H t = 32 , W = N c = 32 ) T\times 32\times 32\times 2(H=H_t=32, W=N_c =32) T×32×32×2(H=Ht?=32,W=Nc?=32) 其中的2通道代表 H H H的实部和虚部。
A ConvlstmCsiNet
- 特征提取中的RNN:在CsiNet的基础上,我们通过在卷积前增加一个ConvLSTM层来细化特征提取模块,并采用RNN的memory function从之前的time steps的输入中学习时间相关性以压缩时间冗余。因此,它可以帮助卷积在特征提取中捕获更多有用的时间信息。
ConvLSTM的主要结构:
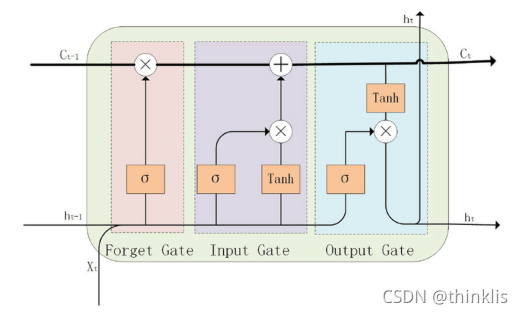
包括forget gate, input gate, output gate
对于特征压缩和特征解压缩模块参考RecCsiNet,使用两个平行的行结构,即全连接和LSTM层,来reshape成 M M M长的码字。将合并后的码字作为编码器的输出,并利用对称结构将其解压缩回 N N N长度,将其reshape成两个 32 × 32 32\times32 32×32大小的特征。
2)特征恢复中的深度可分离卷积:在特征恢复模块中,所有的标准卷积被深度可分离卷积(DS-Conv)替换,这种替换不仅减少了参数两,而且有助于RefineNet实现更好的性能和更高的恢复精度。
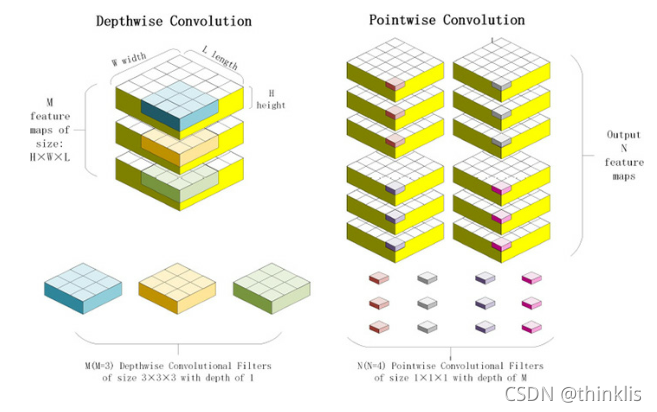
B ConvlstmCsiNet中解耦的时空特征提取
为了进一步细化ConvlstmCsiNet,重点关注特征提取模块中的时空特征表示。ConvLSTM先提取cell中的空就按特征,然后循环cell形成时间序列,从某种意义上来说,这表明提取空间特征和时间特征之间有一定程度的独立性。在3D卷积中研究列这种独立性。
我们使用Pseudo-3D(P3D)代替卷积层进行特征提取。
P3D的关键思想是分别捕捉时间和空间域中的特征。
设计了三种P3D块的设计
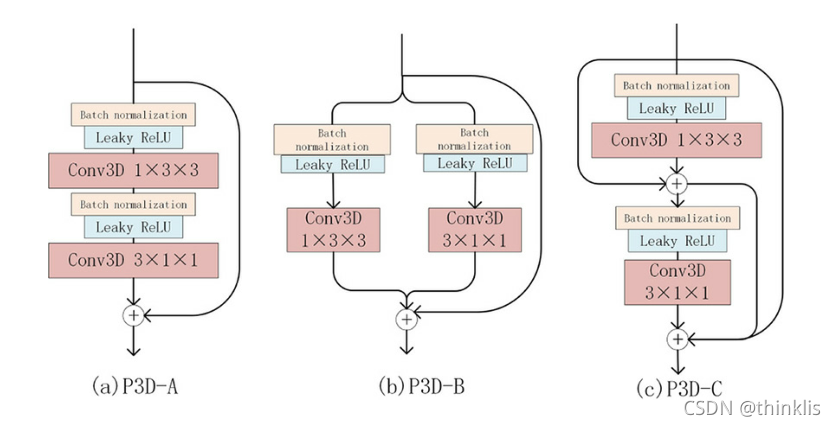
表1 是模型的复杂性分析

4 Experiments numeral results
归一化均方误差 N M S E NMSE NMSE
余弦相似度 ρ \rho ρ
只与CsiNet进行了对比。NMSE的值太小,所以使用 l o g ( N M S E ) log(NMSE) log(NMSE) 去表示。
5 Conclusion
在特征提取和恢复模块中分别采用RNN和深度可分卷积,提出了一种新的CSI反馈网络结构。此外,我们还通过研究解耦的时空卷积表示来设计特征提取部分,该表示被证明优于标准的Conv3D卷积。实验结果表明,该方法能够提高RecCsiNet的恢复鲁棒性、准确性和质量。这种架构具有在真实的多输入多输出系统上实际部署的潜力。