描述性统计分析概述
- python原始的数据类型:字符型、逻辑型、数值型、复数型。
- 从统计方面来看,数据分为三种类型:名义型、等级型、连续型
- 名义变量:性别、民族等,没有顺序之分,名义变量不一定是字符类型
- 等级变量:有顺序之分,可以是字符也可是数值型,差值没有意义。
- 连续变量:只能是数值型,连续变量的差值是有意义的。
注:连续变量可以当作等级变量用,等级变量也可以当成连续变量,连续变量会产生很多噪音,分组换为等级变量会消除噪音。
- 在统计学中,名义变量只有两个统计量:频次和百分比
- 在统计学中,连续变量的统计量:
- 集中趋势(位置):均值、中位数、众数
- 离散程度(分散程度):方差、标准差、极差、四分位差等。
- 偏离程度:右偏函数、对称函数、左偏函数(少见)
注:离散程度即离开均值的程度,可以通过观察图像得知。
5. 分布函数
- 正态分布:对称函数,如人的身高等。
- 泊松分布:如网页点击量、队伍长度。
- 伽码分布:如灾难对我们造成的经济损失。
- 对数正态分布:是右偏最严重的函数,如收入、利润等。
| - | 描述性统计 | 建模、预测 |
|---|---|---|
| 右偏严重的函数(对数正态分布、伽马分布) | 选用中位数为统计量 | 对原始数据取对数,使其成为对数正态分布 |
| 右偏不严重的函数(正态分布、泊松分布) | 选用均值为统计量 | 选用正态分布函数 |
- 判断函数是否右偏:
(1)利用数据画直方图,中位数<均值则右偏
(2)计算偏度,偏度大于1的右偏严重。
示例
查看北京和上海的收入分布情况
步骤一:判断是否右偏严重。
做描述性统计分析的话,右偏函数选用中位数作为集中水平,右偏不严重的函数选用均值作为集中水平。
步骤二:看离散程度,一般是标准差。
描述统计总结
- 分类变量:(维度指标)指时间、年度等,分类变量又包括名义变量和等级变量。
- 连续变量:(度量指标)利润、收入、利润率
| - | 分析 | 可视化 |
|---|---|---|
| 一个分类变量 | value_counts() | 柱形图 |
| 两个分类变量 | pd.crosstab(snd.districts,snd.school) | 标准化堆叠柱形图 |
| 一个连续变量 | agg(['mean','std','skew']) | 直方图 |
| 一个分类+一个连续 | snd.price.groupby(snd.district).sum() | 柱形图、条形图、盒须图 |
| 两个分类+一个连续 | snd.pivot_table(values='',index='',columns=',aggfunc=np.mean) | 分类柱形图 |
一个分类变量
#引入包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import os
import matplotlib
#找到文件夹,读取文件
os.chdir(r'E:\数据与脚本\4describe')
snd = pd.read_csv('SndHsPr.csv')
snd
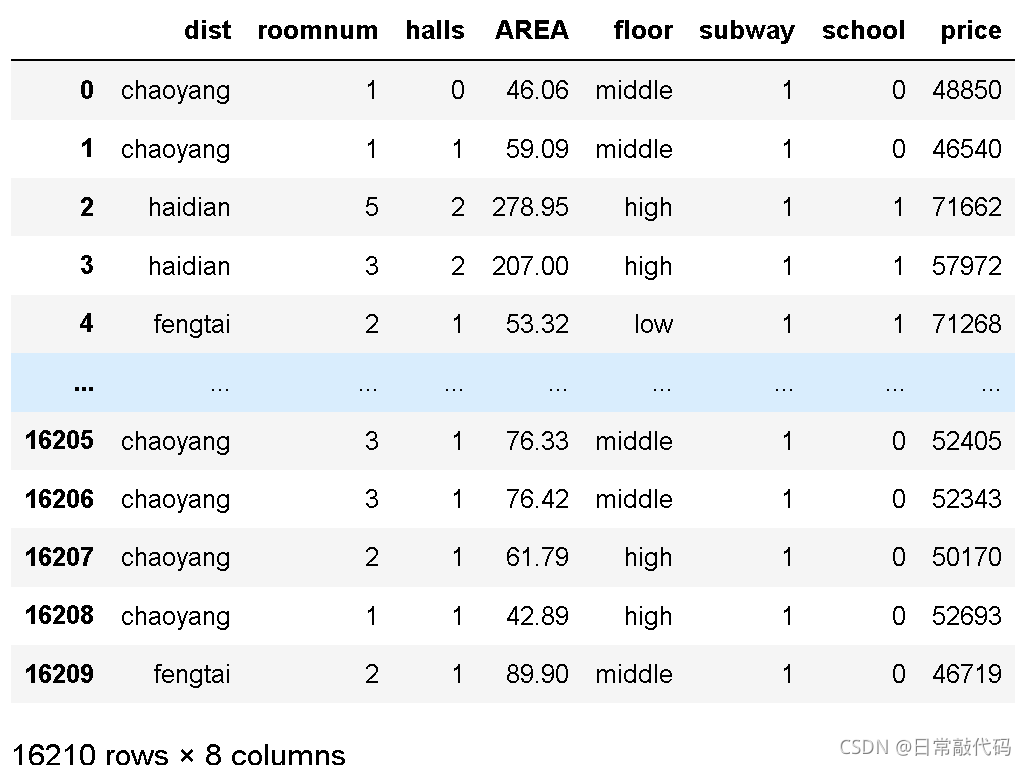
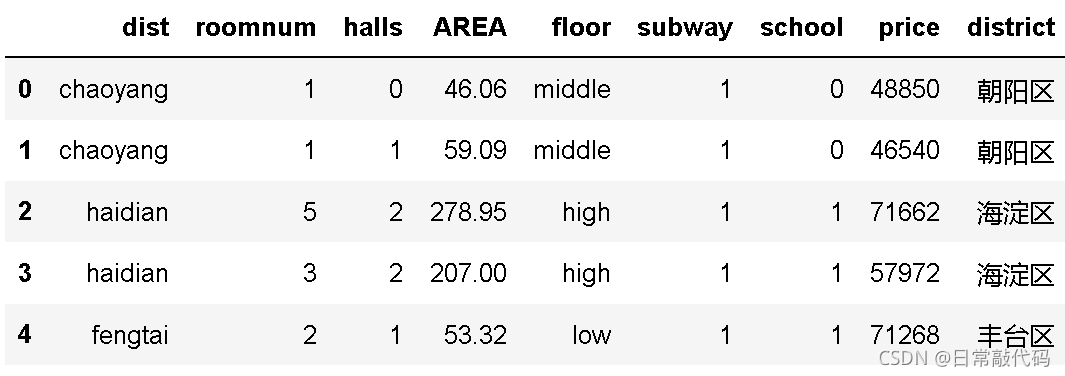
district = {'fengtai':'丰台区','haidian':'海淀区','chaoyang':'朝阳区','dongcheng':'东城区','xicheng':'西城区','shijingshan':'石景山区'}
# 取字典中的元素
snd['district'] = snd.dist.map(district)
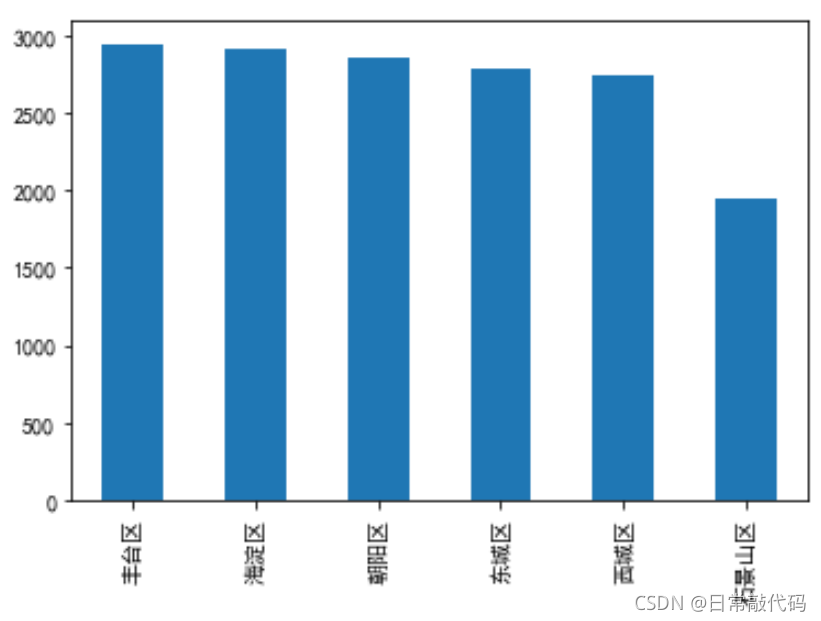
snd.district.value_counts()

- 可视化(
plot(kind='类型'))
# 显示中文
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['Simhei']# 之人默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号‘-’显示为方块的问题
snd.district.value_counts().plot(kind='bar')
一个连续变量
- 统计量
snd.price.mean() #均值
snd.price.median() #中位数,中位数<均值所以是右偏函数
snd.price.std()# 标准差:比较离散程度的时候有用,一个标准差没有用
snd.price.skew() #判断是否右偏,>1 表示严重右偏
snd.price.quantile([0.01,0.5,0.99])# 取分位点的
#一次聚合多个统计量
snd.price.agg(['mean','median','sum','std','skew'])
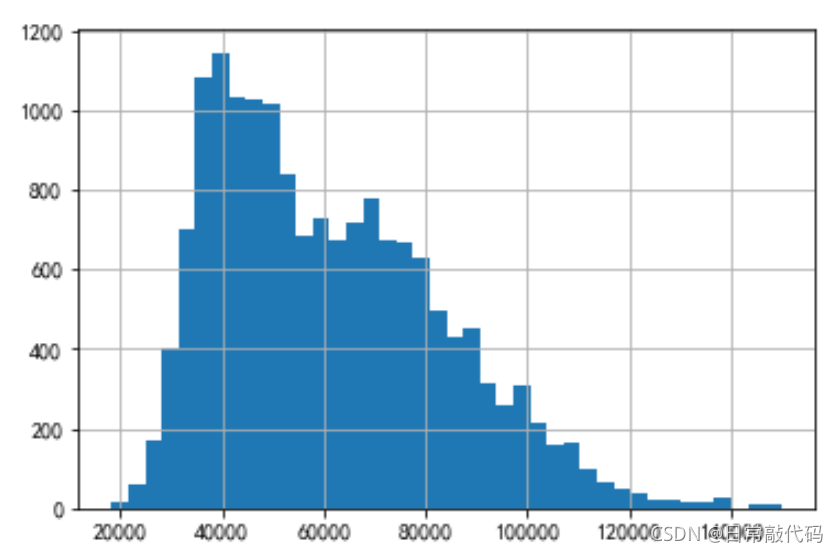
- 直方图(观察右偏与否)
snd.price.hist(bins=40)# 分40组
两个分类变量
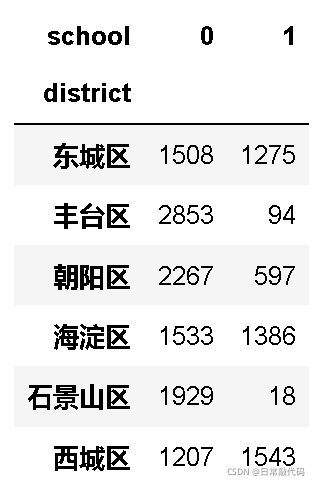
- 频次表
sub_sch = pd.crosstab(snd.district,snd.school)
sub_sch
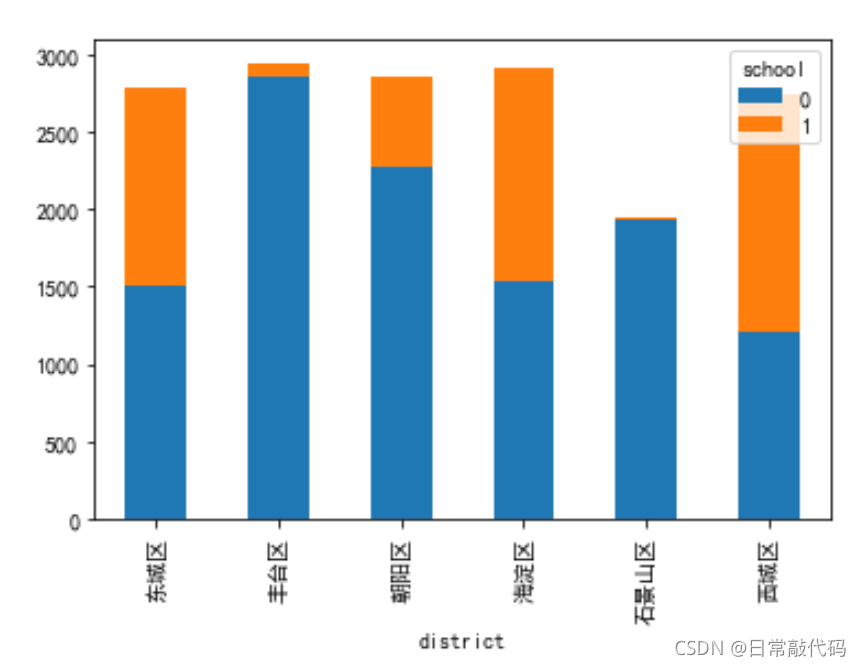
- 堆叠柱形图:只能看出样本量,不能对比样本占比情况。
sub_sch.plot(kind='bar',stacked=True)
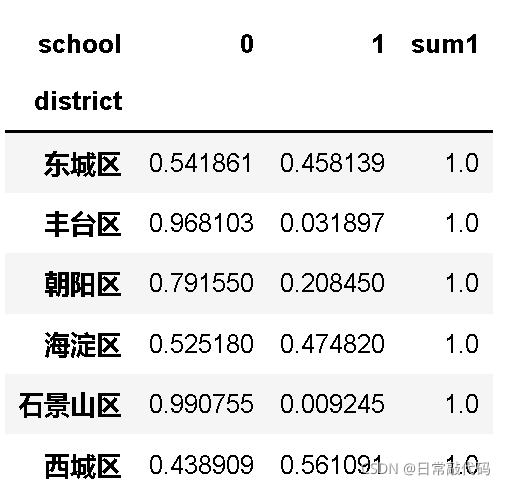
- 标准化堆叠柱形图:标准化堆叠柱形图可以看出占比情况,样本量的大小用柱子的胖瘦代替。
sub_sch["sum1"]=sub_sch.sum(1) #加和成为一列
#按行求百分比
sub_sch = sub_sch.div(sub_sch.sum1,axis = 0)#除法得到百分比
from stack2dim import *
stack2dim(snd,i='district',j='school')
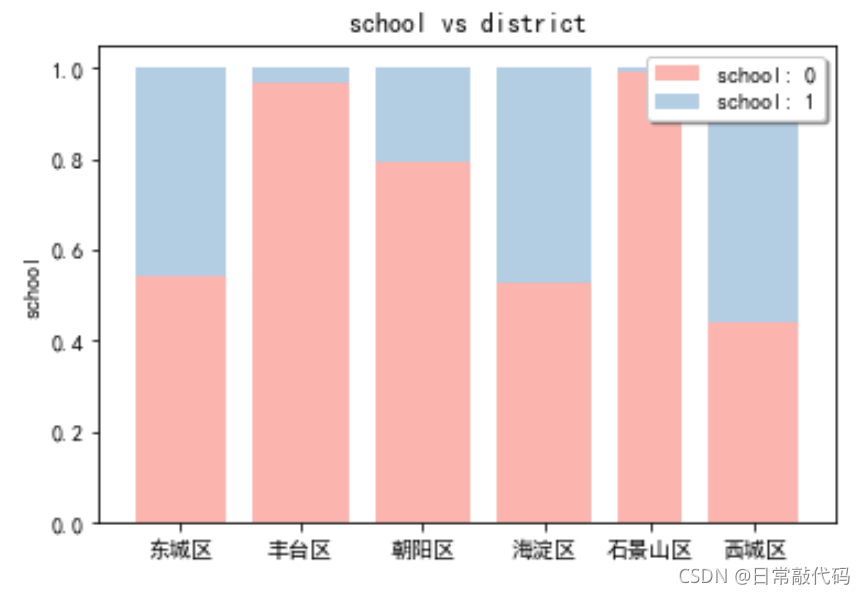
分类变量和连续变量
按照分类变量分组对连续变量求统计量
- 柱形图
#柱形图
snd.price.groupby(snd.district),mean().plot(kind='bar')#price为连续变量,district是分类变量
- 条形图
snd.price.groupby(snd.district).mean().sort_values(ascending=True).plot(kind='barh')
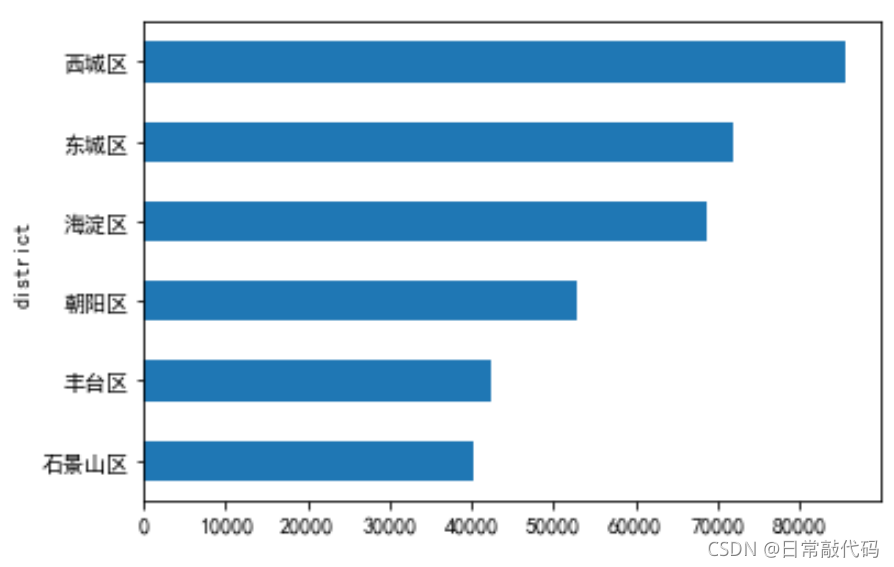
- 分类盒须图:比较不同分类水平上的连续变量变化情况(比较中位数)
sns.boxplot(x = 'district', y = 'price', data = snd)
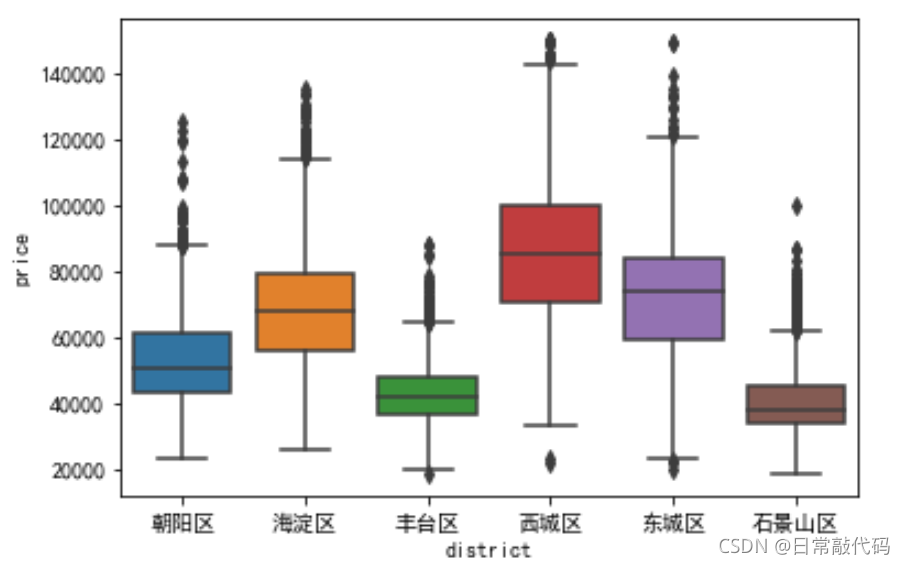
汇总表:两个分类变量+一个连续变量
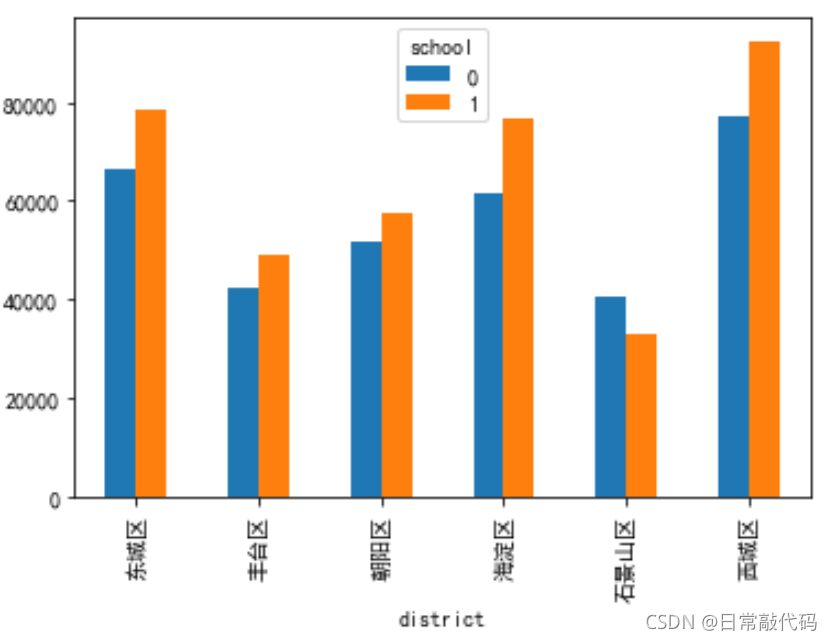
snd.pivot_table(values='price', index='district', columns='school', aggfunc=np.mean)
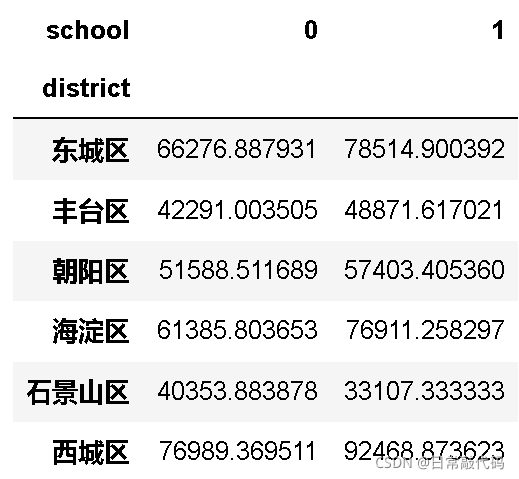
- 可视化
snd.pivot_table(values='price', index='district', columns='school', aggfunc=np.mean).plot(kind = 'bar')