[人工智能]SVM的原理

SVM的基本概念

支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。支持向量机方法是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度，Accuracy）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力（或称泛化能力）。
其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

1）线性分类

如果需要分类的数据都是线性可分的，那么只需要用f(x)=wx+b的直线将其分开即可。

该法被称为线性分类器。
一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面（hyper plane）

• 函数间隔

在超平面wx+b=0确定的情况下，|wx+b|能够表示点x到距离超平面的远近，而通过观察wx+b的符号与类标记y的符号是否一致可判断分类是否正确，所以，可以用(y(w*x+b))的正负性来判定或表示分类的正确性。于此，我们便引出了函数间隔（functional margin）的概念。

• 最大间隔分类器
  对一个数据点进行分类，当超平面离数据点的“间隔”越大，分类的确信度（confidence）也越大。所以，为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。
  

2）非线性分类

刚才的情况是二维平面上的，如果问题在三维甚至高维该怎么处理呢
答案是 将数据放到高维度上再进行分割

当f(x)=x时，这组数据是个直线，如上半部分，但是当我把这组数据变为f(x)=x^2时，这组数据就变成了下半部分的样子，也就可以被红线所分割。

比如说，我这里有一组三维的数据X=（x1,x2,x3），线性不可分割，因此我需要将他转换到六维空间去。因此我们可以假设六个维度分别是：x1,x2,x3,x1^2,x1x2,x1x3，当然还能继续展开，但是六维的话这样就足够了。

核函数

我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去。但进一步，如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的，而且内积方式复杂度太大。此时，核函数就隆重登场了，核函数的价值在于它虽然也是讲特征进行从低维到高维的转换，但核函数绝就绝在它事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算。

所以，解决问题的关键就在于核函数，关于核函数的定义如下：

几种常用核函数：

h度多项式核函数（Polynomial Kernel of Degree h）

高斯径向基和函数（Gaussian radial basis function Kernel）

S型核函数（Sigmoid function Kernel）

图像分类，通常使用高斯径向基和函数，因为分类较为平滑，文字不适用高斯径向基和函数。没有标准的答案，可以尝试各种核函数，根据精确度判定。

拉格朗日乘子法

1）无约束条件

这是最简单的情况，解决方法通常是函数对变量求导，令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
2）等式约束条件

拉格朗日乘子法的求解流程大概包括以下几个步骤：
　　　1. 构造拉格朗日函数
　　　2. 解变量的偏导方程
　　　3. 代入目标函数即可
　　　
设目标函数为f(x)，约束条件为h_k(x)，形如:

  　　s.t. 表示subject to ，“受限于”的意思，l表示有l个约束条件。

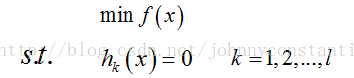
首先定义拉格朗日函数F(x)：

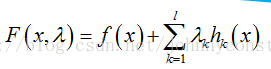
然后解变量的偏导方程：

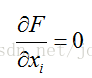
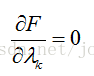
三）、不等式约束条件
不等式约束条件转变为等式约束条件，引入松弛变量，将松弛变量也是为优化变量。

不等式约束相比于等式约束，要复杂一点，而且通常情况下，不等式约束和等式约束总喜欢一起出现，在这里，为了更好的解决该问题，除了拉格朗日乘子外，我们引入了KKT条件。
　　把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + ag(x)+bh(x)，

• KKT条件

KKT条件是说最优值必须满足以下条件：

1）L(a, b, x)对x求导为零；

2）h(x) =0;

3）a*g(x) = 0;
KKT条件详细推导过程如下：

参考文章：https://blog.csdn.net/qq_40036484/article/details/80457800?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522163006369316780255294624%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=163006369316780255294624&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_allfirst_rank_v2~hot_rank-3-80457800.pc_search_result_cache&utm_term=%E6%8B%89%E6%A0%BC%E6%9C%97%E6%97%A5%E4%B9%98%E5%AD%90%E6%B3%95&spm=1018.2226.3001.4187

SMO

序列最小最优化算法SMO可以实现SVM的高效学习。
他将凸二次规划的对偶问题不断的分解为子问题并求解，进而达到求解原问题的目的。
参考文章：https://blog.csdn.net/luoshixian099/article/details/51227754

代码

线性基础：

from sklearn import svm 
  
x = [[2,0,1],[1,1,2],[2,3,3]] 
y = [0,0,1] #分类标记 
clf = svm.SVC(kernel = 'linear') #SVM模块，svc,线性核函数 
clf.fit(x,y) 
  
print(clf) 
  
print(clf.support_vectors_) #支持向量点 
  
print(clf.support_) #支持向量点的索引 
  
print(clf.n_support_) #每个class有几个支持向量点 
  
print(clf.predict([2,0,3])) #预测

线性展示图：

from sklearn import svm 
import numpy as np 
import matplotlib.pyplot as plt 
  
np.random.seed(0) 
x = np.r_[np.random.randn(20,2)-[2,2],np.random.randn(20,2)+[2,2]] #正态分布来产生数字,20行2列*2 
y = [0]*20+[1]*20 #20个class0，20个class1 
  
clf = svm.SVC(kernel='linear') 
clf.fit(x,y) 
  
w = clf.coef_[0] #获取w 
a = -w[0]/w[1] #斜率 
#画图划线 
xx = np.linspace(-5,5) #(-5,5)之间x的值 
yy = a*xx-(clf.intercept_[0])/w[1] #xx带入y，截距 
  
#画出与点相切的线 
b = clf.support_vectors_[0] 
yy_down = a*xx+(b[1]-a*b[0]) 
b = clf.support_vectors_[-1] 
yy_up = a*xx+(b[1]-a*b[0]) 
  
print("W:",w) 
print("a:",a) 
  
print("support_vectors_:",clf.support_vectors_) 
print("clf.coef_:",clf.coef_) 
  
plt.figure(figsize=(8,4)) 
plt.plot(xx,yy) 
plt.plot(xx,yy_down) 
plt.plot(xx,yy_up) 
plt.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80) 
plt.scatter(x[:,0],x[:,1],c=y,cmap=plt.cm.Paired) #[:，0]列切片，第0列 
  
plt.axis('tight') 
  
plt.show()