一、How Expressive are Graph Neural Networks?

现在已经有了各种GNN模型。如GCN，GraphSAGE。那么问题来了，哪个模型更好？哪个模型的表达力更强（即区分节点的能力）？GCN采用求和函数作为聚合函数，GraphSAGE采用max函数。哪个更好呢？本章是一些理论性分析。
在这里插入图片描述

1.local neighborhood structures

下图中，用颜色表示节点的特征信息。不同颜色代表不同的特征信息。当一个图中所有节点特征都相同时，怎么区分节点呢？比如下图中1、2节点附近的结构相同个，而1与其他节点的附近的结构都不相同。如何使得网络能区分开这有不同结构信息的节点呢？
在这里插入图片描述
例如节点1和5的区分，直接用度就可以区分；1和4有相同的度，但这俩节点的二阶邻居不同。
根据GNN的算法，它在哪些情况下能区分，哪些情况下不能区分呢？为了回答这个问题，首先说明一下Computational graph的概念（其实早就出现过了）
如，一个两层的GNN中，节点1的计算图就是：
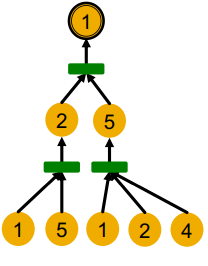
在这里插入图片描述
层就是消息传播了几次。
这样，能发现节点1和节点2的计算图是一样的：

但是GNN只能看到节点的特征，看不到节点的编号（id），因此变成了这样：

因此，GNN会给节点1和2生成相同的表示（嵌入）。
广泛地讲，一个邻居的邻居，定义了它的计算图：
在这里插入图片描述
节点A的计算图就等同于以节点A为根的树：

具有表达力的GNN，将不同的rooted subtree structures映射到不同的表示：

会议单射函数的概念：（injective function）将不同的自变量映射到不同的因变量上。

expressive GNN应该满足单射的特征：
在这里插入图片描述
如何得知GNN的表示力？一个关键的观察点是，信息是从一个个子树的叶子节点，一点点传递到树根的。如果GNN算法能全部保留这些信息，那么它就是有区分力，即有表示力的。比如下图中，左边是从2+3个邻居聚合，右图是从1+3个邻居聚合。这显然包含了不同的信息。因此如果算法能保留这些所有的信息，那么就是一个好算法。
在这里插入图片描述
如果GNN的每一步聚合，都能具有区分度，都能保留所有信息，那么整个模型也是具有区分度的：

二、Designing the Most Powerful Graph Neural Network

这里讲怎么设计一个具有表示力的模型。
关键思想：聚合函数应该满足单射的特征。越是单射，越有表示力。
这里可以将邻居聚合过程，抽象化，抽象成为一个a function over a multi-set 的问题：具体来说，就是一个作用于带有重复元素的集合的函数。使其应该满足单射的特征。
在这里插入图片描述
上图表示，邻居聚合过程，可以抽象称为一个a function over a multi-set 的问题。

1.GCN的聚合操作

GCN采用的是求均值，relu激活：
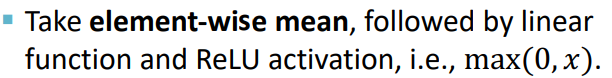
在这里插入图片描述
但是这种方法作用于如下数据时，会失效：（左图两个节点，右图四个。但是求均值后就得出了相同的表示）

2.GraphSAGE

采用的是MaxPool方法：
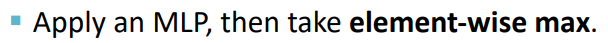
在这里插入图片描述
示例是下图。用MLP对每个节点做映射，然后得出one-hot向量。然后对每个维度求Max。发现这三种输入对应同样的输出：

3.本节小结

在这里插入图片描述

4.设计一个满足单射性质的NN

首先是一个定理，即多重集合上的单射函数都能表示为如下的形式：
在这里插入图片描述
解释一下：即任意一个多重集合上的单射函数，都可以拆分成两部分。一部分是作用于单个元素的函数 $f$ ，这是个单射函数（比如将不同颜色的节点，映射为不同的one-hot向量）；另一部分是非线性映射函数 $\phi$ 。
在这里插入图片描述
但是如何定义这两个函数？采用的是MLP。这里用到了Universal Approximation Theorem（万能近似定理）：带有一层隐藏层的MLP可以近似任何连续函数。又因为我们事先不知道采用什么函数好。所以采用MLP，让模型自己去学习：
在这里插入图片描述
这样，就得到了使用NN的模型：(即 $f$ 和 $\phi$ 都是MLP，通常隐藏层的维度100-500即可)

这样，就得到了有名的GIN：

这个模型是最具有表示力的，满足单射的特征（没有像GCN那种映射失败的情形）
然后，可以分析出，GIN就是神经网络版的 WL graph kernel：这里多了一步同构性判断：如果两个图有相同的节点颜色集合，那么这俩图是同构isomorphic的：
在这里插入图片描述
神经网络是在用神经网络模拟WL graph kernel的方法：

具体来说，就是用NN来模拟在这个元组上的单射函数：

而元组上的单射函数又可以被写为如下形式：

完整的GIN模型：
给定一个图和节点的初始特征向量，GIN迭代如下公式：
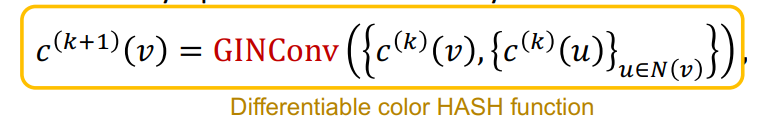
在这里插入图片描述
其中GINConv就是一个可导的单射（哈希）函数。 $K$ 次迭代后，其收集了 $K$ 阶邻居的信息。
因此，GIN可以视为一个可导版本的WL graph Kernel。前者使用节点向量做表示，用GINConvert更新参数；后者用颜色作为节点表示，用HASH函数做更新操作。
在这里插入图片描述
GIN的两个优点是：

因此，这两个方法的表示效果是等价的。

三、本章总结

首先是解释了表示力的概念（即区分力），然后是计算图的概念。然后将表示力的问题转化到设计聚合函数上，然后将聚合函数的问题转化为多重集上的函数单射问题，然后讲了GCN采用的均值聚合函数和GraphSAGE采用的Max函数有什么问题，然后提出了一个多重集上的定理，用于分析GIN的表示力。最后分析了GIN和WL核的表示力是等价的。
在这里插入图片描述