[人工智能]SVM算法学习笔记

什么是SVM算法

SVM（support vector machine）支持向量机，是一个有监督的学习模型，通常用来进行模式识别、分类(异常值检测)以及回归分析。

Hard margin

将两类通过一个阈值而分类开，对于二维来说就是找一条线，三维找一个面，多维找一个超平面

Hard margin:距离超平面最近的点的间隔最大

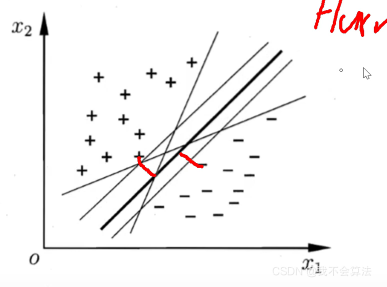
最优线：

在SVM中最优分割面(超平面)就是：能使支持向量和超平面最小距离的最大值

在样本空间中，划分超平面可通过一个线性方程来描述：
$${\omega }^{T}x+b=0$$
其中$\omega$=（${\omega }_1$;${\omega }_2$;…;${\omega }_3$）为法向量，决定了超平面的方向，b为位移项，决定了超平面与原点之间的距离，划分超平面可被法向量$\omega$和位移b确定

样本空间中任意一点x到超平面（$\omega$，b）的距离可写为

若超平面对应方程为${\omega }^{T}x+b=0$

若超平面能够将训练样本正确分类，对于任意（$x_i$，$y_i$），若$y_i$ = +1，则有${\omega }^T{x}_i+b>0$；若$y_i$ = -1，则有${\omega }^T{x}_i+b<0$

、

距离超平面最近的这几个训练样本点使得上式成立，它们被称为"支持向量"（support vector）,两个异类支持向量到超平面的距离之和为

、

它们被称为“间隔”(margin)

求最大间隔，也就是要找在满足参数$\omega$?和b（$y_i（{\omega }^T{x}_i+b）>=1$?）的同时，使得$\gamma$?最大

通过转化：

在满足参数$\omega$和b（$y_i（{\omega }^T{x}_i+b）>=1$）的同时，使得${\omega }^2/2$?最小?

求解：拉格朗日乘子法

拉格朗日乘子法

假如有方程：

$x^{2}y=3$

图像：

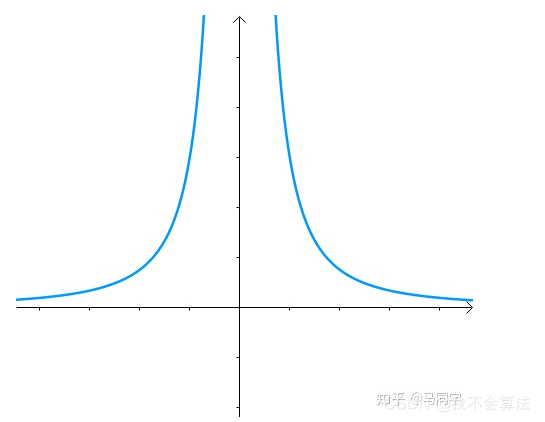
求其上的点与原点的最小距离

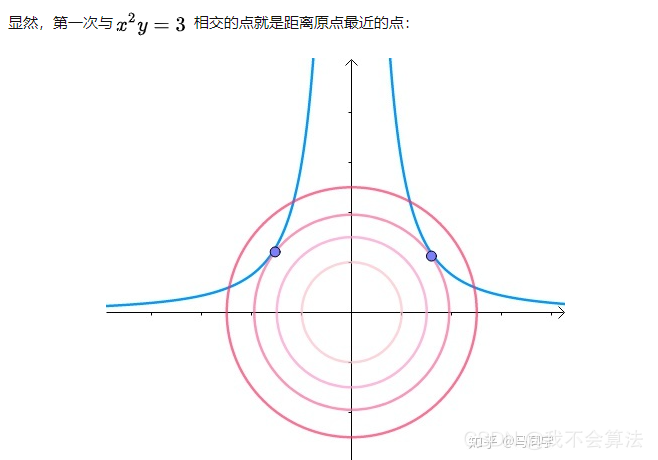
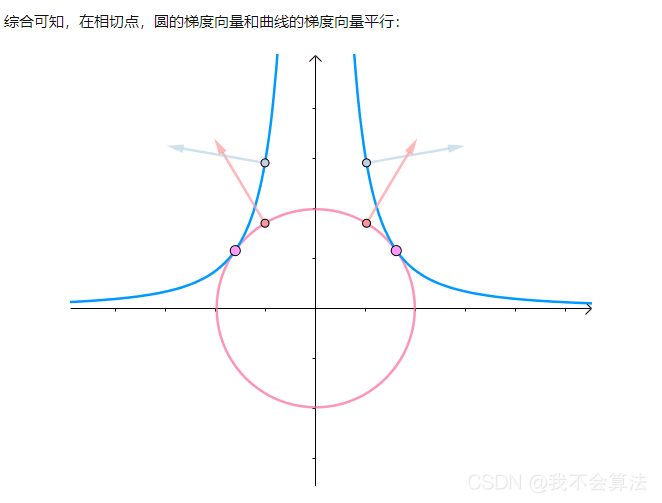
即梯度向量平行，用数学符号表示：

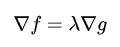
因此：

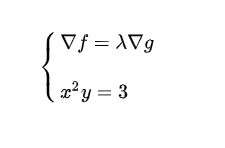
也就是函数f在g的约束下的极值问题可表示为：

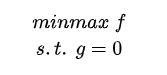
可列出方程求解：

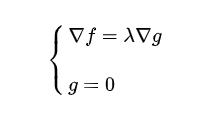
这就是拉格朗日乘子法

类似地：如果有多个约束条件

即可求得解

以上在高等数学拉格朗日求极值有详解

KKT条件

Soft Margin

在Hard margin的基础上允许有一点错误（loss）
采用Soft Margin可以防止过拟合

折页损失（high loss）

一般当z<1时分类错误，允许有一点损失，loss=1-yi(wTxi + b)
当z>=1时分类正确，loss = 0

线性分类：

一般地像一维、二维、三维这些可以通过阈值、直线、平面或超平面就能将数据划分的被称为线性分类

非线性分类

数据大多数情况都不可能是线性的，那如何分割非线性数据呢？

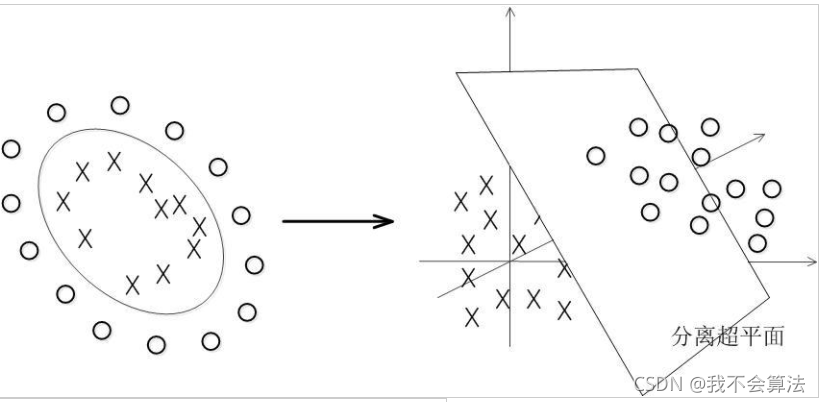
方法就是将数据处理后放到更高的维度上进行分割：

当f(x)=x时，这组数据是个直线，如上半部分，但是当我把这组数据变为f(x)=x^2时，这组数据就变成了下半部分的样子，也就可以被红线所分割。

比如说，我这里有一组三维的数据X=（x1,x2,x3），线性不可分割，因此我需要将他转换到六维空间去。因此我们可以假设六个维度分别是：x1,x2,x3,x1^2,x1x2,x1x3，当然还能继续展开，但是六维的话这样就足够了。
新的决策超平面：d(Z)=WZ+b，解出W和b后带入方程，因此这组数据的超平面应该是：d(Z)=w1x1+w2x2+w3x3+w4*x1^2+w5x1x2+w6x1x3+b但是又有个新问题，转换高纬度一般是以内积（dot product）的方式进行的，但是内积的算法复杂度非常大。

几种常用核函数：

1. h度多项式核函数（Polynomial Kernel of Degree h）
2. 高斯径向基和函数（Gaussian radial basis function Kernel）
3. S型核函数（Sigmoid function Kernel）

图像分类，通常使用高斯径向基和函数，因为分类较为平滑，文字不适用高斯径向基和函数。没有标准的答案，可以尝试各种核函数，根据精确度判定。

SVM与其他机器学习算法对比

SVM算法具有以下特征：

1. SVM可以表示为凸优化问题，因此可以利用已知的有效算法发现目标函数的全局最小值。而其他分类方法都采用一种基于贪心学习的策略来搜索假设空间，这种方法一般只能获得局部最优解。
2. SVM通过最大化决策边界的边缘来实现控制模型的能力。尽管如此，用户必须提供其他参数，如使用核函数类型和引入松弛变量等。
3. SVM一般只能用在二类问题，对于多类问题效果不好。

四种核函数的分类效果（代码）

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt

# 设置子图数量
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(7, 7))
ax0, ax1, ax2, ax3 = axes.flatten()

# 准备训练样本
x = [[1, 8], [3, 20], [1, 15], [3, 35], [5, 35], [4, 40], [7, 80], [6, 49]]
y = [1, 1, -1, -1, 1, -1, -1, 1]

# 设置子图的标题
titles = ['LinearSVC (linear kernel)',
          'SVC with polynomial (degree 3) kernel',
          'SVC with RBF kernel',  # 这个是默认的
          'SVC with Sigmoid kernel']
# 生成随机试验数据(15行2列)
rdm_arr = np.random.randint(1, 15, size=(15, 2))


def drawPoint(ax, clf, tn):
    # 绘制样本点
    for i in x:
        ax.set_title(titles[tn])
        res = clf.predict(np.array(i).reshape(1, -1))
        if res > 0:
            ax.scatter(i[0], i[1], c='r', marker='*')
        else:
            ax.scatter(i[0], i[1], c='g', marker='*')
    # 绘制实验点
    for i in rdm_arr:
        res = clf.predict(np.array(i).reshape(1, -1))
        if res > 0:
            ax.scatter(i[0], i[1], c='r', marker='.')
        else:
            ax.scatter(i[0], i[1], c='g', marker='.')


if __name__ == "__main__":
    # 选择核函数
    for n in range(0, 4):
        if n == 0:
            clf = svm.SVC(kernel='linear').fit(x, y)
            drawPoint(ax0, clf, 0)
        elif n == 1:
            clf = svm.SVC(kernel='poly', degree=3).fit(x, y)
            drawPoint(ax1, clf, 1)
        elif n == 2:
            clf = svm.SVC(kernel='rbf').fit(x, y)
            drawPoint(ax2, clf, 2)
        else:
            clf = svm.SVC(kernel='sigmoid').fit(x, y)
            drawPoint(ax3, clf, 3)
    plt.show()

结果：

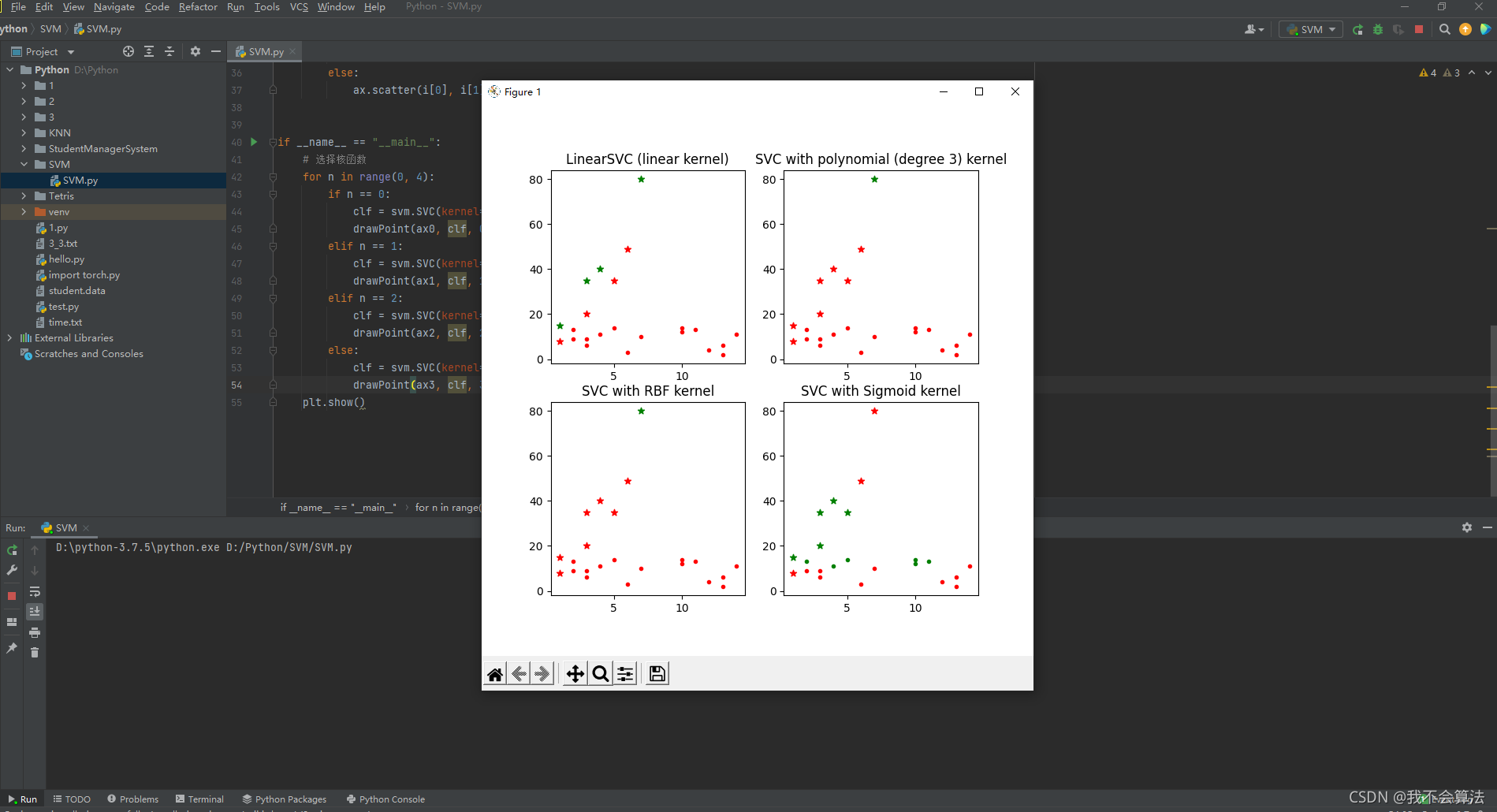
注意：
核函数(这里简单介绍了sklearn中svm的四个核函数，还有precomputed及自定义的)

1. LinearSVC：主要用于线性可分的情形。参数少，速度快，对于一般数据，分类效果已经很理想
2. RBF:主要用于线性不可分的情形。参数多，分类结果非常依赖于参数
3. polynomial:多项式函数,degree 表示多项式的程度-----支持非线性分类
4. Sigmoid：在生物学中常见的S型的函数，也称为S型生长曲线