摘要:蝗虫算法( Grasshopper Optimization Algorithm,GOA ) 是 由 Saremi 等[1]于2017 年提出的一种元启发式仿生优化算法,具有较高的搜索效率和较快的收敛速度,且算法本身特殊的自适应机制能够很好地平衡全局和局部搜索过程,具有较好的寻优精度。
1.算法原理
根据蝗虫算法模拟蝗虫在自然界中的种群迁移和觅食行为将搜索分为: 探索和开发。对该过程进行数学建模,蝗虫算法的数学公式如下:
X_{i}=S_{i}+G_{i}+A_{i}Xi?=Si?+Gi?+Ai?
式中:?X_{i}Xi?为第?ii?个蝗虫的位置;?S_{i}Si?为个体间相互影响力;?G_{i}Gi?为第?ii?个蝗虫受到的重力;?A_{i}Ai?为第ii?个蝗虫受到的风力。蝗虫的社会作用对蝗虫位置的影响最大。S_{i}Si?计算如下:
S_{i}=\sum_{j=1,j\neq i}^{N}s(d_{ij})\bold{d_{ij}}Si?=j=1,j?=i∑N?s(dij?)dij?
式中:?d_{ij} = |x_{i}-x_{j}|dij?=∣xi??xj?∣为第 i 个蝗虫与第 j 个蝗虫之间的距离;\bold{d_{ij}}=(x_{j}-x{i})/d_{ij}dij?=(xj??xi)/dij?为第 i 个蝗虫指向第 j 个蝗虫的单位向量; s 为社会力量,其为负数时表示相互排斥,为正数时表示相互吸引,计算方法如下:
s=fe^{\frac {-r}{l}}-e^{-r}s=fel?r??e?r
式中:?ff?为吸引强度;?ll?为吸引长度尺度。当?l=1. 5,f= 0. 5l=1.5,f=0.5?时,函数$ s$ 的曲线显示了蝗虫之间的相互作用力( 吸引和排斥)。
G_{i}Gi?可计算如下:
G_{i}=-ge_{g}Gi?=?geg?
式中:?gg?为重力常数;?e_{g}eg?为指向地球中心的单位向量。
A_{i}Ai?可计算如下:
A_{i}=ue_{w}Ai?=uew?
式中:uu?为风力常量;?e_{w}ew?为指向风向的单位向量。于是X_{i}Xi?可表示为:
X_{i}=\sum_{j=1,j\neq i}^{N}s(|x_{j}-x{i}|)\frac {x_{j}-x_{i}}{d_{ij}}-ge_{g}+ue_{w}Xi?=j=1,j?=i∑N?s(∣xj??xi∣)dij?xj??xi???geg?+uew?
通常当蝗虫群到达舒适区时,虫群仍旧没有收敛,为了适应优化问题的求解,协调全局和局部优化过程,通过引入参数以区分不同阶段的寻优。改进后的数学模型如下:
X_{i}=\sum_{j=1,j\neq i}^{N}c\frac {ub_{d}-lb_{d}}{2}s(|x_{j}-x{i}|)\frac {x_{j}-x_{i}}{d_{ij}}+T_{d}Xi?=j=1,j?=i∑N?c2ubd??lbd??s(∣xj??xi∣)dij?xj??xi??+Td?
式中:?cc?为递减系数,决定着舒适区、斥力区和吸引区的大小;?NN?为蝗虫数量;?ub_{d}ubd?和?lb_{d}lbd?分别为函数s(r)=fe^{\frac {-r}{l}}-e^{-r}s(r)=fel?r??e?r在dd?维空间上的上下界;T_{d}Td?为目前为止蝗虫位置在dd?维空间上的最佳解。式中不考虑重力影响,且假定风向总指向最优解。内部的?cc?有助于减少蝗虫之间的斥力或吸引力,且与迭代次数成正比,外部的?cc?随着迭代次数
的增加会减少对目标周围的搜索区域。利用下式(更新参数cc,随着迭代次数的增加,减少全局搜索,并增加局部精度搜索。
c = c_{max}-n\frac {c_{max}-c_{min}}{L}c=cmax??nLcmax??cmin??
式中:?c_maxcm?ax为最大值;?c_mincm?in为最小值;?nn?为当前迭代次数;?LL?为 最 大 迭 代 次 数; 本 文 取c_{max}= 1,c_{min}=0.00004cmax?=1,cmin?=0.00004。
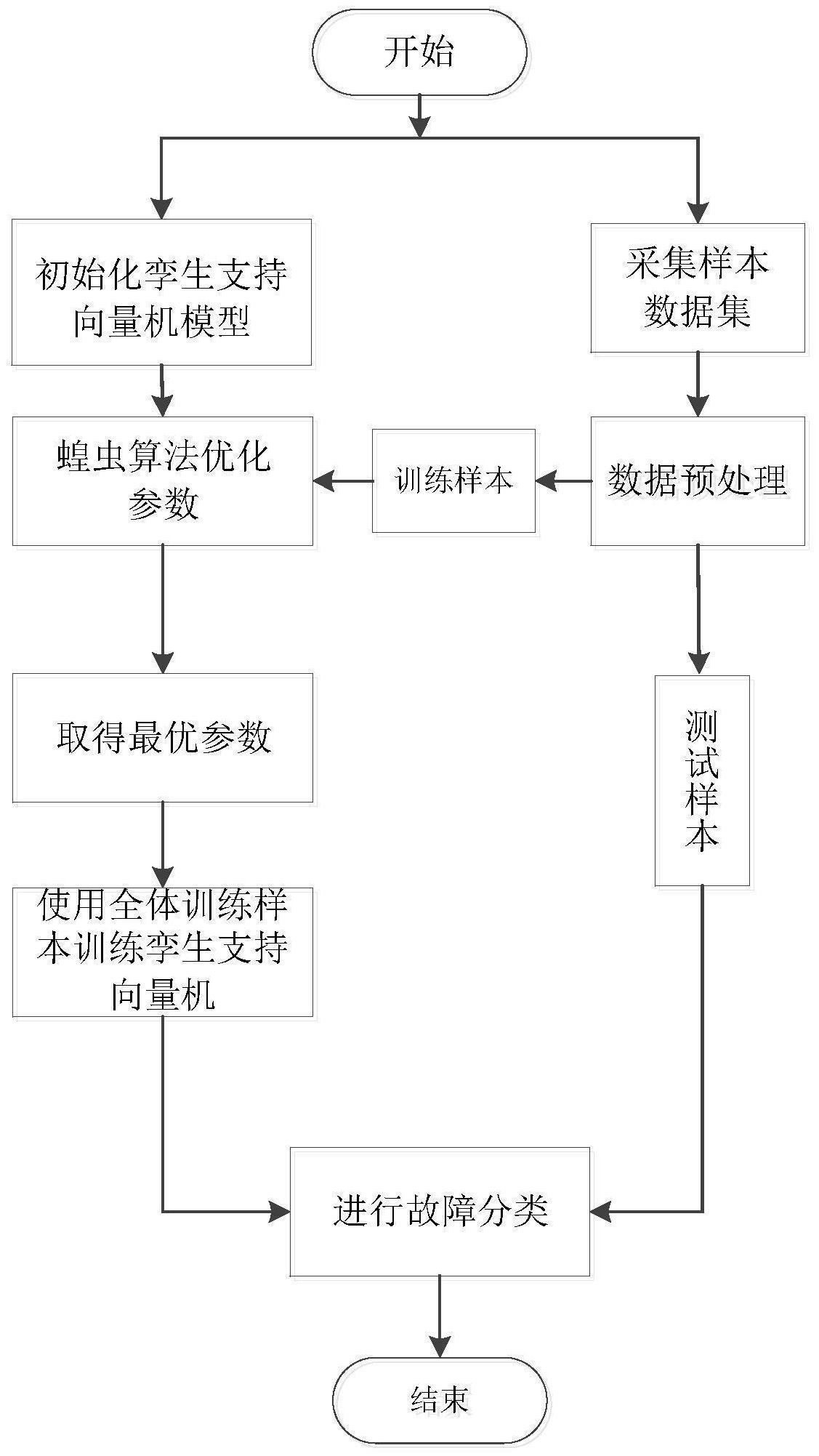
2.算法流程
算法步骤如下:
( 1) 初始化。首先初始化蝗虫种群 和算法中各参数。
( 2) 计算每个蝗虫的适应度;
( 3) 计算当前最佳适应度;
( 4) 判断是否达到迭代次数,若达到,则程序结束,当前的全局最优解的位置即为最优解
( 5) 更新参数 c;
( 6) 标准化蝗虫之间的距离,归一化区间为[1,4];
( 7) 更新蝗虫的位置,并计算更新后的蝗虫适应度,与历史最佳进行比较,若适应度优于历史最佳,则更新,否则不更新;
( 8) 更新迭代次数,并返回到( 4)
% The Grasshopper Optimization Algorithm
function [TargetFitness,TargetPosition,Convergence_curve,Trajectories,fitness_history, position_history]=GOA(N, Max_iter, lb,ub, dim, fobj)
tic
disp('GOA is now estimating the global optimum for your problem....')
flag=0;
if size(ub,1)==1
ub=ones(dim,1)*ub;
lb=ones(dim,1)*lb;
end
if (rem(dim,2)~=0) % this algorithm should be run with a even number of variables. This line is to handle odd number of variables
dim = dim+1;
ub = [ub; 100];
lb = [lb; -100];
flag=1;
end
%Initialize the population of grasshoppers
GrassHopperPositions=initialization(N,dim,ub,lb);
GrassHopperFitness = zeros(1,N);
fitness_history=zeros(N,Max_iter);
position_history=zeros(N,Max_iter,dim);
Convergence_curve=zeros(1,Max_iter);
Trajectories=zeros(N,Max_iter);
cMax=1;
cMin=0.00004;
%Calculate the fitness of initial grasshoppers
for i=1:size(GrassHopperPositions,1)
if flag == 1
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,1:end-1));
else
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,:));
end
fitness_history(i,1)=GrassHopperFitness(1,i);
position_history(i,1,:)=GrassHopperPositions(i,:);
Trajectories(:,1)=GrassHopperPositions(:,1);
end
[sorted_fitness,sorted_indexes]=sort(GrassHopperFitness);
% Find the best grasshopper (target) in the first population
for newindex=1:N
Sorted_grasshopper(newindex,:)=GrassHopperPositions(sorted_indexes(newindex),:);
end
TargetPosition=Sorted_grasshopper(1,:);
TargetFitness=sorted_fitness(1);
% Main loop
l=2; % Start from the second iteration since the first iteration was dedicated to calculating the fitness of antlions
while l<Max_iter+1
c=cMax-l*((cMax-cMin)/Max_iter); % Eq. (2.8) in the paper
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:size(GrassHopperPositions,1)
temp= GrassHopperPositions';
% for k=1:2:dim
S_i=zeros(dim,1);
for j=1:N
if i~=j
Dist=distance(temp(:,j), temp(:,i)); % Calculate the distance between two grasshoppers
r_ij_vec=(temp(:,j)-temp(:,i))/(Dist+eps); % xj-xi/dij in Eq. (2.7)
xj_xi=2+rem(Dist,2); % |xjd - xid| in Eq. (2.7)
s_ij=((ub - lb)*c/2)*S_func(xj_xi).*r_ij_vec; % The first part inside the big bracket in Eq. (2.7)
S_i=S_i+s_ij;
end
end
S_i_total = S_i;
% end
X_new = c * S_i_total'+ (TargetPosition); % Eq. (2.7) in the paper
GrassHopperPositions_temp(i,:)=X_new';
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% GrassHopperPositions
GrassHopperPositions=GrassHopperPositions_temp;
for i=1:size(GrassHopperPositions,1)
% Relocate grasshoppers that go outside the search space
Tp=GrassHopperPositions(i,:)>ub';Tm=GrassHopperPositions(i,:)<lb';GrassHopperPositions(i,:)=(GrassHopperPositions(i,:).*(~(Tp+Tm)))+ub'.*Tp+lb'.*Tm;
% Calculating the objective values for all grasshoppers
if flag == 1
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,1:end-1));
else
GrassHopperFitness(1,i)=fobj(GrassHopperPositions(i,:));
end
fitness_history(i,l)=GrassHopperFitness(1,i);
position_history(i,l,:)=GrassHopperPositions(i,:);
Trajectories(:,l)=GrassHopperPositions(:,1);
% Update the target
if GrassHopperFitness(1,i)<TargetFitness
TargetPosition=GrassHopperPositions(i,:);
TargetFitness=GrassHopperFitness(1,i);
end
end
Convergence_curve(l)=TargetFitness;
disp(['In iteration #', num2str(l), ' , target''s objective = ', num2str(TargetFitness)])
l = l + 1;
end
if (flag==1)
TargetPosition = TargetPosition(1:dim-1);
end
time=toc
蝗虫优化算法的适应度曲线和优化后的c、g参数值,交叉验证CV准确率

?蝗虫优化算法优化后的实际类型与识别类型对比图像

从适应度曲线来看,蝗虫优化算法的收敛速度很快,但后期发生聚群行为(可能陷入局部最优)。SVM对红酒数据集的分类准确率一般为97%上下,故起到了优化的效果。
参考文献: [1]Shahrzad, Saremi, Seyedali, et al. Grasshopper Optimisation Algorithm: Theory and application[J]. Advances in Engineering Software, 2017.