[人工智能]AlphaGo 原理讲解

1. 棋盘编码器

AlphaGo所采用的棋盘编码器为 19×19×49 的特征张量，其中前48个平面用于策略网络的训练，最后一个平面用于价值网络的训练。前48个平面包含11种概念，其更多地利用了围棋专有的定式，例如它在特征集合中引入了征子和引征的概念。最后一个平面用来表示当前执子方。

AlphaGo的棋盘编码器也采用了二元特征，它用8个平面分别代表每个棋子是否有1口、2口…和至少8口气。AlphaGo 所使用的特征平面的分类和解释如下：

2. AlphaGo的网络架构

AlphaGo一共使用了三个神经网络，包括2两个策略网络和1个价值网络。其中策略网络分为快策略网络和强策略网络。快策略网络的主要作用是为了在保证一定高的预测准确率的情况下同时能够非常迅速地做出动作预测。与之相反，强策略网络的优化目标是准确率而不是预测速度，其网络更深且预测效果比快策略网络好2倍。最后价值网络用来评判当前棋盘状态的好坏，其使用强策略网络的自我对弈产生的数据集训练出来的。接下来我们分别看一下这三种网络。

(1)强策略网络

强策略网络一共有13层卷机网络，且在整个网络的训练过程中，都保留的原始的19&times19的大小，因此我们需要对中间卷机层进行paddinga操作。此外第一个层卷积核的大小为5，剩下12层的卷积核的大小为3，最后一层的卷积核大小为1，且只有一个过滤器。关于激活函数，前12层都采用Relu激活函数，最后一层由于要得出每个位置的概率值，因此采用softmax 激活函数。强策略网络使用keras实现如下：

model = Sequential()
    model.add(
        Conv2D(192, 5, input_shape=input_shape, padding="same", data_format='channels_first', activation='relu')
    )
 
    for i in range(2, 12):
        model.add(
            Conv2D(192, 3, padding='same', data_format='channels_first', activation='relu')
        )

    model.add(
        Conv2D(filters=1, kernel_size=1, padding='same', data_format='channels_first', activation='softmax')
        )
    model.add(Flatten())

(2)快策略网络

由于快策略网络的主要目的是构建一个比强策略网络更小的网络，从而能够进行快速评估，因此读者可以自行创建一个简易的网络从而实现此功能，这里就不做示例。

(3)价值网络

价值网络总共有16层卷机网络，其中前12层与强策略网络完全一致，第13层是一个额外的卷机层，与第2～12层的结构一致，而第14层的卷积核大小为1，并且有一个过滤器。最后是两层稠密层，倒是第二层共有256个输出，采用ReLU几何函数；最后一层只有一个输出，表示当前状态的价值，采用tanh激活函数。需要注意的是价值网路的输入维度和策略网络的输入维度不同，前面我们知道价值网络的输入比策略网络的输入多一层特征值用来记录当前执子方。价值网络使用keras实现如下：

model = Sequential()
    model.add(
        Conv2D(192, 5, input_shape=input_shape, padding="same", data_format='channels_first', activation='relu')
    )

    for i in range(2, 13):
        model.add(
            Conv2D(192, 3, padding='same', data_format='channels_first', activation='relu')
        )
        
    model.add(
        Conv2D(filters=1, kernel_size=1, padding='same', data_format='channels_first', activation='relu')
        )
    model.add(Flatten())
    model.add(Dense(256, activation='relu'))
    model.add(Dense(1, activation='tanh'))

3. 策略网络的训练

(1) 监督学习初始化策略网络(behavior cloning)

AlphaGo最开始使用监督学习方法对策略网络进行预训练，每个游戏状态编码为一个张量，而训练所使用的标签是一个与棋盘尺寸相同的向量，并在实际动作落子处填入1，其余位置为0，训练流程图如下：

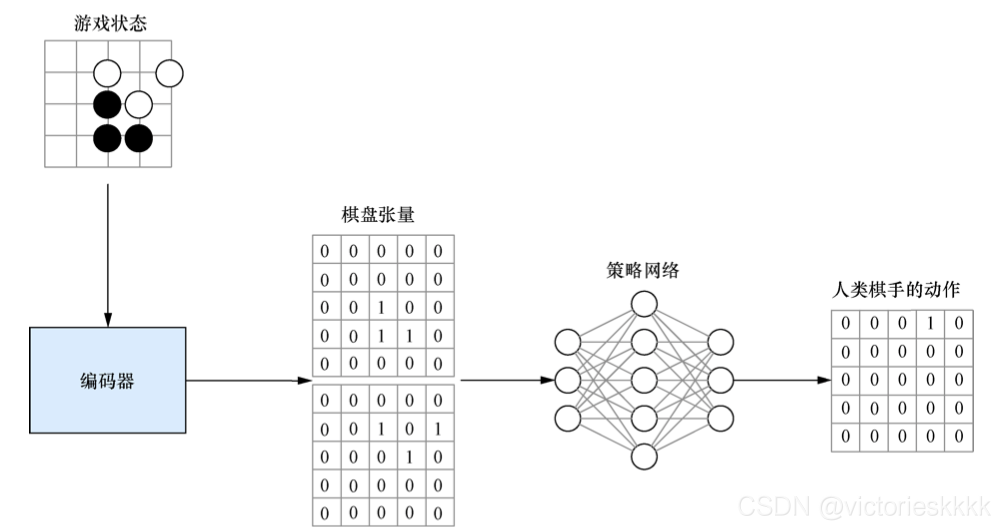
我们用同样的方法训练强策略网络和快策略网络，通过监督学习训练的网络已经可以很大概率地打败业余玩家了，但是如果想要赢得职业玩家还需要继续进行提升。

(2) 自我对弈(self-play)

DeepMind使用多个不同版本的强策略网络与当前最强版本的强策略网络进行对弈，这么做能够防止过拟合并且在总体上能够得到更好的表现。在这里我们采用更简单的方法，直接让上面训练好的强策略网络进行自我对弈，机器人对弈的代码如下：

def simulate_game(black_player, white_player, board_size):
    game = GameState.new_game(board_size)
    moves = []
    agents = {
        Player.black: black_player,
        Player.white: white_player,
    }

    while not game.is_over():
        next_move = agents[game.next_player].select_move(game)
        moves.append(next_move)
        game = game.after_move(next_move)

    game_result = scoring.compute_game_result(game)

    return game_result

def experience_simulator(num_games, agent1, agent2):
    collector1 = experience.ExperienceCollector()
    collector2 = experience.ExperienceCollector()

    color = Player.black
    for i in range(num_games):
        collector1.begin_episode()
        collector2.begin_episode()
        agent1.set_collector(collector1)
        agent2.set_collector(collector2)

        if color == Player.black:
            black_player, white_player = agent1, agent2
        else:
            black_player, white_player = agent2, agent1
        game_record = simulate_game(black_player, white_player)
        if game_record.winner == color:
            collector1.complete_episode(reward=1)
            collector2.complete_episode(reward=-1)
        else:
            collector1.complete_episode(reward=-1)
            collector2.complete_episode(reward=1)
        color = color.other

    return experience.combine_experience([collector1, collector2])

代码中的‘ExperienceCollector’类用于储存和处理对弈过程中生成的棋谱状态，相应的动作以及动作奖励的数据序列$(s_1,a_1,r_1,s_2,...,s_t,a_t)$。其中每个动作的奖励取决于胜负。具体而言，如果此轮博弈player获得胜利，那么player所有的动作奖励值都为1，否则为-1。每一轮次比赛结束后，（状态，动作，奖励）序列值都会存储到player和opponent的经验收集器中，双方的经验值可以结合一起用于之后训练的数据集。在实现指定轮次的对弈之后，我们用其生成的经验值训练强策略网络。

(3) 策略剃度算法训练策略网络(Policy Gradient)

在讨论策略梯度算法之前，我们先了解一下策略学习(Policy- Based Reinforcement Learning), 策略学习通过使用神经网络估计策略函数(policy function), 从而进一步的估计状态价值函数(state-value function):
$$V\left(s;\theta \right)=\sum _a\pi \left(a\mid s;\theta \right).Q_{\pi }\left(s,a\right)$$
policy- based的核心思想就是通过更新$\theta$值从而最大化状态价值函数的期望，而更新$\theta$的方法就是策略梯度上升方法，虽然称为策略梯度但是本质上可以理解为随机梯度，其随机性来自于状态$s$。策略梯度算法的推导公式如下：
$$g\left(a,\theta \right)=\frac{?\log \pi \left(a|s;\theta \right)}{?\theta }?Q_{\pi }\left(s,a\right)$$
$g\left(a,\theta \right)$是$\frac{?V\left(s;\theta \right)}{?\theta }$的无偏估计，其中$Q_{\pi }\left(s,a\right)$时动作价值函数，其大小是对在状态$s$下动作$a$的打分。在推导出策略梯度之后，我们使用梯度上升更新$\theta$值：
$${\theta }_{t+1}={\theta }_t+\beta ?g\left(a_t,{\theta }_t\right)$$
在AlphaGo中运用策略梯度训练强策略网络的时候，每一个动作的奖励值(-1 or 1)，就是公式中的$Q_{\pi }\left(s,a\right)$的对于每一个特定状态下相应动作的无偏估计。根据公式，在用keras实现的时候，损失函数我们使用‘categorical_crossentropy’更新参数。示例代码如下：

    def train(self, experience):
        self._model.compile(loss='categorical_crossentropy',
                            optimizers=keras.optimizers.SGD(lr=self.lr, clipnorm=self.clip))
        n = experience.states.shape[0]
        num_moves = self._encoder.board_width * self._encoder.board_height
        y = np.zeros((n, num_moves))
        for i in range(n):
            action = experience.actions[i]
            reward = experience.rewards[i]
            y[i][action] = reward

        self._model.fit(experience.states, y, batch_size=self.batch_size, epochs=self.epochs)

2016年，AlphaGo对战当时最强的开源围棋机器人Pachi（相当于业余2段）的获胜概率达到了85%，令人惊叹；虽然之前有人仅用卷积网络进行过动作预测，但对战Pachi的获胜率没有超过10%，可见，自我博弈对于围棋机器人的能力提升要远胜于单纯使用监督学习。

4. 价值网络的训练

除了训练策略网络选择下棋的位置，Alphago还运用了价值网络模拟状态价值函数来评估当前状态的好坏，以此来辅助蒙特卡洛树搜索（MCTS）。状态价值函数的定义如下：
$$V_{\pi }\left(s\right)=E\left(U_t|S_t=s\right)$$
其中当$U_t$的值接近1时表示的那前状态接近于赢的状态；当其值接近于-1时表示当前棋局状态接近于输。因此神经网络的输入应该是编码后的当前棋局，而输出结果是一个位于$[?1,1]$之间的数值。我们使用训练的数据是之前策略网络自我博弈存储的棋盘数据，训练代码如下：

    def train(self, experience):
        self.model.compile(loss='mse', optimizer=keras.optimizers.SGD(lr=self.lr))
        n = experience.state_values.shape[0]
        y = np.zeros((n,))
        for i in range(n):
            reward = experience.rewards[i]
            y[i] = 1 if reward > 0 else -1

        self.model.fit(experience.state_values, y, batch_size=self.batch_size, epochs=self.epochs)

5. 蒙特卡洛树搜索（MCTS）

再介绍AlphaGo如何将策略网络和价值网络用语优化蒙特卡洛树搜索算法之前，我们先来了解蒙特卡洛树搜索的搜索思想。蒙特卡洛树搜索的是蒙特卡洛算法族的一员，蒙特卡洛算法的中心思想就是利用随机性来分析并解决一些复杂的问题。

我们以下围棋为例，把模拟进行的每一个随机棋局称为一次推演(rollout)。前面说过蒙特卡洛算法的核心思想就是其随机性，通过选择随机动作来建立一个良好的策略咋看似乎是不可行的，但是如果让两个势均力敌的AI进行博弈，当游戏进行了几百轮，几千轮甚至几万轮，如果发现一方持续比另一方赢的多，那么我们可以认为对于这种游戏，前者相较于后者掌握了一些优势，至于为什么会有这样的结果并不需要我们深入探究。我们可以将类似的思想应用于围棋。一般地，蒙特卡洛树搜索包括三个步骤：

$[1]$ 搜索新的棋局，并将新的棋局添加到MCTS树中；
$[2]$ 从新添加的棋局开始模拟随机对弈；
$[3]$ 根据随机对弈的结果更新树节点的统计数据。

接下来我们分别探究这三个步骤。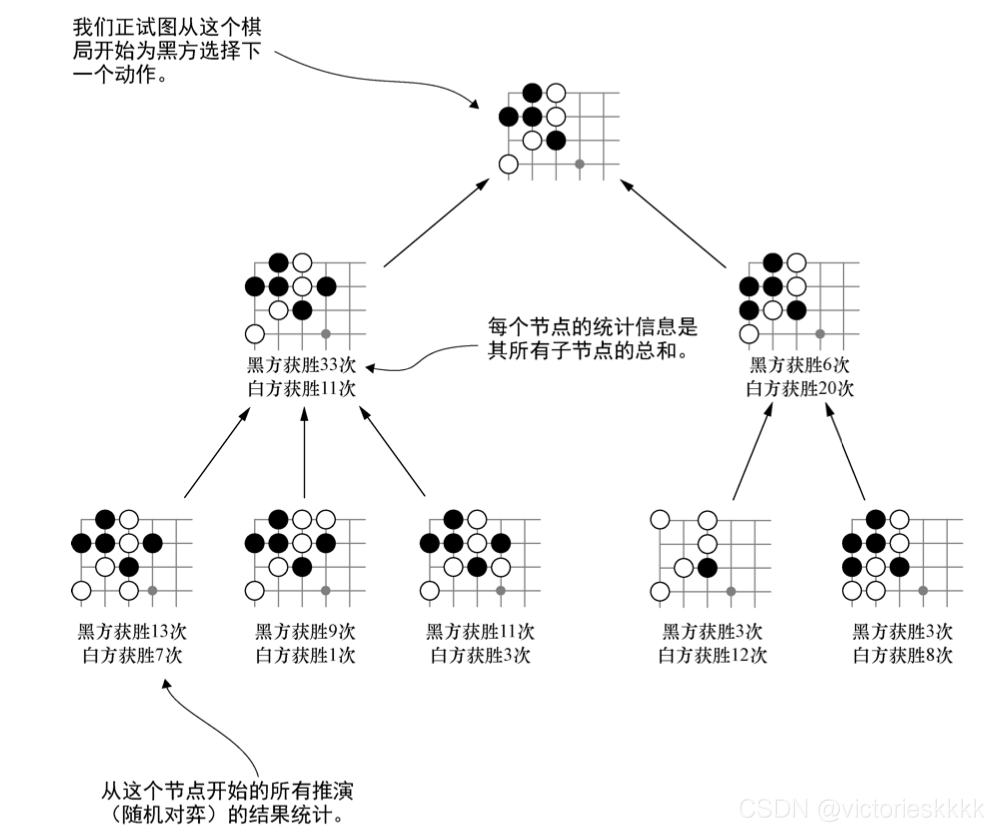

(1) 搜索新的棋局

每一轮开始我们都要在搜索树中添加一个新的节点，即AI都要执行一个新的动作。然而由于每一个回合中AI能够运用的时间是有限的，如果在动作A上多消耗一次推演，那么在动作B上就要少消耗一次推演时间。因此，为了获得最佳效果，我们需要采取适当的策略来选取要添加新节点的叶节点位置，这里我们采用搜索树置信区间上界公式(Upper Confidence bound for Trees formula)，简称UCT公式，来决定选择继续探索哪个分支。接下来我们先来了解一下UCT公式。

UCT公式

和常见的搜索算法一样，MCTS也存在深度搜索和广度搜索之间的平衡问题。在这里，我们分别称之为深入挖掘(exploitation)和广泛搜索(exploration)。

深入挖掘：即想要对迄今为止搜索到的比较理想的动作进行更加深入的挖掘，随着你对这些分支进行更加多的推演，你的估算也会更加准确，误报率也会下降；在MCTS中，我们使用获胜百分率$w$作为深入挖掘的目标，其定义为当前棋局下一个执子方所赢得的总次数与当前节点所储存的总推演数之间的比值。

广泛搜索：另一方面，如果一些节点只被访问了几次，那么他所得到的评估就可能有很大的误差。因此我们可以把更多的时间花在提高那些访问次数少的节点的推演次数。根据以上定义，广泛搜索的目标函数如下：
$$\sqrt{\frac{\log N}{n}}$$
其中$n$代表从当前节点开始的所有推演数，$N$表示所有分支的推演总数，也就是根节点中存储的推演总数。

将以上两种目标结合起来，就构成了UCT公式：
$$w+c\sqrt{\frac{\log N}{n}}$$
这里参数$c$被称为温度参数，当温度高时，搜索将更发散，当温度较低时，搜索将更集中，一般取值为0.5。

定义好UCT公式之后我们就可以计算每个叶节点的UCT值，从而选择数值较高的叶节点进行扩展。

(2) 模拟对弈并更新各节点数据

从新添加的节点开始，每一回合随机选择一个合法的动作，直到棋局终盘。然后进行终盘结算，并得到获胜方，之后将这次推演的结果记录在新节点中，并回溯之前的祖先节点更新他们的数据。

上述过程是MCTS的一次推演，再经过固定轮次的推演之后我们就可以停止推演，这个时候我们回到原先的叶节点，选择获胜率$w$最高的那个动作即可。

6. AlphaGo改进版的蒙特卡洛树搜索

前面我们已经介绍了蒙特卡洛树搜索的算法思想，AlphaGo将神经网络和蒙特卡洛树搜索相结合，是的树搜索算法更加强大。接下来我们将分点介绍改进版的蒙特卡洛树搜索和传统MCTS算法的区别。

(1) 选择下一步动作(selection)

假设当前处于叶节点状态为$s$, 那么对于所有的合法动作，我们按照以下公式计算各个动作的得分，选取最高得分的动作为下一步动作：
$$a^{\prime }=argma{x}_a\left[Q\left(a\right)+\frac{\pi \left(a\mid s;\theta \right)}{1+N\left(a\right)}\right]$$
其中$\pi \left(a\mid s;\theta \right)$是强策略网络给动作$a$的打分，这里我们将这些概率分布称为该动作的先验概率（prior probability)。$N(a)$是出于当前状态下，动作$a$被选择的次数。整个这一项我们可以这么理解：选择动作$a$在当前状态下对后续越有利，$\pi \left(a\mid s;\theta \right)$的值越大；但是当这个动作被探索很多次之后，也就是$N(a)$越来越大，会导致整个这一项的值变小，从而减少继续探索这个动作的次数。另一项$Q(a)$被称作动作-价值函数，其初始值为0，稍后我们给出其定义。强策略网络预测对各个动作的打分$\pi \left(a\mid s;\theta \right)$的代码实现如下：

    def policy_probabilities(self, game_state):
        encoder = self.policy_agent.encoder
        outputs = self.policy_agent.predict(game_state)
        legal_moves = game_state.legal_moves()
        if not legal_moves:
            return [], []
        encoded_points = [encoder.encode_point(move.point) for move in legal_moves if move.point]
        legal_outputs = outputs[encoded_points]
        # normalize the output probabilities
        normalized_outputs = legal_outputs / np.sum(legal_outputs)

        return legal_moves, normalized_outputs

(2) 扩展搜索树(Expansion)

当我方选择完下一步动作之后，对手也会进行下一步动作。这里我们采用快策略网络模拟对手的动作，并在所有的合法动作之中随机选择一个动作应用到棋盘上，生成新的状态$s_{t+1}$，也就是下一个节点。之后结合快策略网络迅速的推演出让快策略网络自我博弈，直到到达最终棋局。这也是为什么需要快策略网络，因为只有推演速度够快，才能在短时间内完成大量的推演。

我们使用policy_rollout函数用来实现这一快速推演策略，这个函数在每次推演的时候都从快策略网络中选择最强的动作，直至达到最大推演次数，然后查看胜负结果。如果执子方获胜，则返回1；如果对手获胜，则返回-1；否则，返回0。

 def policy_rollout(self, game_state):
        for step in range(self.rollout_limit):
            if game_state.is_over():
                break
            move_probabilities = self.rollout_policy_agent.predict(game_state)
            encoder = self.rollout_policy_agent.encoder
            # filter all the moves and retain all th legal moves  
            valid_moves = [m for index, m in enumerate(move_probabilities)
                           if Move(encoder.decode_point_index(index)) in game_state.legal_moves()]

            max_index, max_value = max(enumerate(valid_moves), key=operator.itemgetter(1))
            max_point = encoder.decode_point_index(max_index)
            move = Move(max_point)
            game_state = game_state.after_move(move)

        next_player = game_state.next_player
        winner = game_state.winner
        if winner is not None:
            return 1 if winner == next_player else -1
        else:
            return 0

(3) 评估叶节点(Evaluation)

AlphaGo评估下一个动作产生的待扩展节点的依据为以下公式：
$$V(s_{t+1})=\lambda ?v(s_{t+1})+(1?\lambda )?r$$
其中r为快搜索策略下得到的棋局终盘时候的结果，其值为1或者-1；$v(s_{t+1})$为之前我们训练的价值网络的输出，它也可以表示在状态$s_{t+1}$的情况下，我们的胜算有多大；$\lambda$默认值为0.1。

因为树搜索挑选动作时要模拟很多局棋局，因次对于每一个棋局，状态$s_{t+1}$都会有很多个对应的$v(s_{t+1})$值，对所有这些值进行累加并除以该节点的访问次数，就得到了我们先前提到的$Q(a_t)$值。注意，这里状态$s_{t+1}$由于对手下棋动作的随机性，所以不一定是同一个状态，因此在计算$Q(a_t)$的时候，各个分支的节点的$V$值是分开进行进行归一化的。

(4) 真正地扩展树节点(Final Decision)

在进行以上步骤之后，我们只需要选择访问计数多的节点作为真正的扩展节点即可。这样的做法是合理的，因为节点计数的访问会随着Q值的提高而增多，在进行了足够多的模拟之后，访问计数就能够成为衡量该动作相对价值的一个良好指标了。选择下一步动作的代码如下：

    def select_move(self, game_state):
        for simulation in range(self.num_simulations):
            current_state = game_state
            node = self.root
            for depth in range(self.depth):
                if not node.children:
                    if current_state.is_over():
                        break
                    moves, probs = self.policy_probabilities(current_state)
                    node.add_children(moves, probs)

                move, node = node.select_child()
                current_state = current_state.after_move(move)

            value = self.value_agent.predict(current_state)
            rollout = self.policy_rollout(current_state)
            weighted_value = (1 - self.lambda_value) * value + self.lambda_value * rollout

            node.update_values(weighted_value)

        move = max(self.root.children, key=lambda move:self.root.children.get(move).visit_conut)
        self.root = AlphaGoNode
        if move in self.root.children:
            self.root = self.root.children[move]
            self.root.parent = None
        return move

本文参考书籍：《深度学习与围棋》