位置编码 - 领略位置编码神奇的风景 - 系列(1)
前文
自从attention在nlp流行之后,不管是在bert还是在transformer,都缺少不了位置编码的身影(position embedding)。主要原因是attention在计算的时候,不管是QK之间的点乘运算,还是attention scores与V之间的点乘运算在训练时都是并行计算的,从逻辑上来说,跟RNN不一样,attention处理时并没有先后之分。
-
当一个句子中出现多个相同的token时,从语义上来说,同一个token在一个句子中的不同位置都有不同的含义。
- 举个例子,“我在苹果公司吃苹果”,这里出现的两个“苹果”明显表达的是两个意思,那么人是怎么区分两个“苹果”之间的含义?
- 最重要的就是根据token之间的位置关系。因为第一个“苹果”和“公司”这个token旁边,所以可以很清楚的知道第一个“苹果”表示的是苹果公司。
- 由于attention计算是点乘计算,所以不同位置的token,都会跟其它位置的token进行内积计算,经过层层的网络,然后计算loss,最后通过反向传播优化参数。这样就会导致在不同位置的token,有着相同的embedding。明显是不符合语义的。
- 举个例子,“我在苹果公司吃苹果”,这里出现的两个“苹果”明显表达的是两个意思,那么人是怎么区分两个“苹果”之间的含义?
-
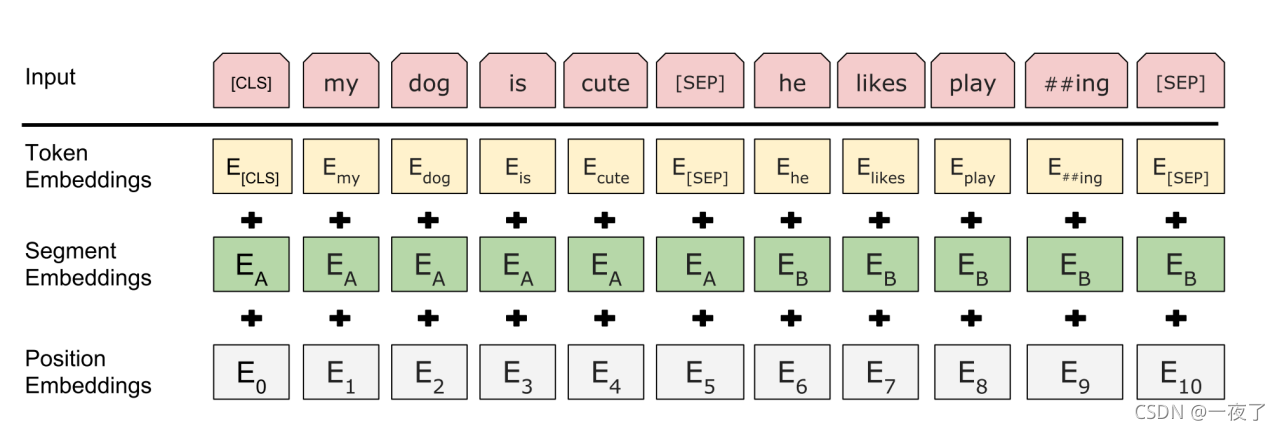
因此,在不同的位置上,相同的token需要有不同的embedding输入。目前,在transformer类似的结构里面,主要是将输入的embedding分为几个部分。大体上可以区分为token embedding与position embedding,当输入模型的时候,就是将二者相加(当然还有其它的处理方式,例如相乘,这里只考虑通用的方法),其中,token embedding表示token的本质含义,而position embedding则表示token的位置编码。由于位置编码在不同位置是不一样的,所以就能让不同位置的token有着不同的含义。当然,除了token embedding和position embedding之外,还有其它的一些embedding,由于与本文无关,这里不过多介绍。
-
自bert与transformer之后,位置编码的发展也是百花齐放,下面我将为大家仔细的介绍不同的位置编码。如果各位读者能从本文中得到一点收获,希望能够点赞,收藏一下,如果有什么问题,也可以评论。

1. 绝对位置编码
1.1 参数式绝对位置编码
顾名思义,参数式绝对位置编码,就是利用可学习的参数来表示绝对位置。
- 什么是绝对位置?:
- 就是不管什么句子,句子的第一个token,位置就是0,第二个token,位置就是1。举个栗子,针对句子“我在苹果公司吃苹果”,其位置编码为:[0,1,2,3,4,5,6,7,8]。其中,“我”的位置编码就是0,‘在’位置编码就是1。
- 什么是参数式?
- 与token的编码一样,可以随机初始化一个变量,然后让模型自己学习位置编码。当然这种方式需要预先设定最大的位置编码长度,比如说max_position_embeddings=512。之后就可以定一个shape为[max_position_embeddings, embedding_size]的variable。最后不同的位置编码one-hot之后,就可以映射到不同的位置编码上。
- bert就是采用这种位置编码方式,这种编码方式首先来说比较的简单,位置编码直接交给模型去学习,同时,也会带来需要大量的数据进行token与position embedding的学习。
1.2 函数式位置编码
函数式位置编码主要是指通过函数来表示不同位置信息。这里主要表示transformer里使用的函数式位置编码方式。
- 公式如下:
P E ( p o s , 2 i ) = sin ? ( p o s / 1000 0 2 i / d model? ) P E ( p o s , 2 i + 1 ) = cos ? ( p o s / 1000 0 2 i / d model? ) \begin{aligned} PE_{(pos, 2i)} &=\sin \left(pos / 10000^{2i / d_{\text {model }}}\right) \\ PE_{(pos, 2i+1)} &=\cos \left(pos / 10000^{2i / d_{\text {model }}}\right) \end{aligned} PE(pos,2i)?PE(pos,2i+1)??=sin(pos/100002i/dmodel??)=cos(pos/100002i/dmodel??)?
其中, p o s pos pos表示token的位置, i i i表示embeding中的某个纬度。 d m o d e l d_{model} dmodel?表示position embedding的纬度大小。 - 为什么使用sin/cos三角函数?
- 原文:We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, P E p o s + k PE_{pos+k} PEpos+k? can be represented as a linear function of P E p o s PE_{pos} PEpos?.
- 证明:
- 假定:
E
∈
R
n
×
d
model?
\boldsymbol{E} \in \mathbb{R}^{\boldsymbol{n} \times d_{\text {model }}}
E∈Rn×dmodel??表示行为n,列为
d
m
o
d
e
l
d_{model}
dmodel?的矩阵。则
E
E
E可定义为:
e ( t ) = E t , j = [ sin ? ( t f 0 , 0 ) , . . . , sin ? ( t f 1 , j ) cos ? ( t f 0 , 0 ) , . . . , cos ? ( t f 1 , j ) sin ? ( t f 1 , 0 ) , . . . , sin ? ( t f 2 , j ) cos ? ( t f 1 , 0 ) , . . . , cos ? ( t f 2 , j ) ? sin ? ( t f d model? 2 ? 1 , 0 ) , . . . , sin ? ( t f d model? 2 , j ) cos ? ( t f d model? 2 ? 1 , 0 ) , . . . , cos ? ( t f d model? 2 , j ) ] e(t)=\boldsymbol{E}_{t,j}=\left[\begin{array}{c} \sin \left(\frac{t}{f_{0,0}}\right),...,\sin\left(\frac{t}{f_{1,j}}\right) \\ \cos \left(\frac{t}{f_{0,0}}\right),...,\cos\left(\frac{t}{f_{1,j}}\right) \\ \sin \left(\frac{t}{f_{1,0}}\right),...,\sin \left(\frac{t}{f_{2,j}}\right) \\ \cos \left(\frac{t}{f_{1,0}}\right),..., \cos \left(\frac{t}{f_{2,j}}\right)\\ \vdots \\ \sin \left(\frac{t}{f_{\frac{d_{\text {model }}}{2}-1,0}}\right),...,\sin \left(\frac{t}{f_{\frac{d_{\text {model }}}{2},j}}\right) \\ \cos \left(\frac{t}{f_{\frac{d_{\text {model }}}{2}-1,0}}\right),...,\cos \left(\frac{t}{f_{\frac{d_{\text {model }}}{2},j}}\right) \end{array}\right] e(t)=Et,j?=????????????????????sin(f0,0?t?),...,sin(f1,j?t?)cos(f0,0?t?),...,cos(f1,j?t?)sin(f1,0?t?),...,sin(f2,j?t?)cos(f1,0?t?),...,cos(f2,j?t?)?sin(f2dmodel????1,0?t?),...,sin(f2dmodel???,j?t?)cos(f2dmodel????1,0?t?),...,cos(f2dmodel???,j?t?)?????????????????????
其中, E t , : E_{t,:} Et,:?每一列可以表示为 sin ? ( t f t ) \sin\left(\frac{t}{f_{t}}\right) sin(ft?t?), f m = 1 λ m : = 1000 0 2 m d model? f_{m}=\frac{1}{\lambda_{m}}:=10000^{\frac{2 m}{d_{\text {model }}}} fm?=λm?1?:=10000dmodel??2m?。 - 问题可以转化为:存在一个线性转置
T
(
k
)
∈
R
d
model?
×
d
model?
\boldsymbol{T}^{(k)} \in \mathbb{R}^{d_{\text {model }} \times d_{\text {model }}}
T(k)∈Rdmodel??×dmodel??,使得对于序列中的任意有效位置
t
∈
{
1
,
…
,
n
?
k
}
t \in\{1, \ldots, n-k\}
t∈{1,…,n?k}的任意的位置偏移量
k
∈
{
1
,
…
,
n
}
k \in\{1, \ldots, n\}
k∈{1,…,n},下式均成立:
T ( k ) E t , : = E t + k , (1) \boldsymbol{T}^{(k)} \boldsymbol{E}_{t,:}=\boldsymbol{E}_{t+k,} \tag{1} T(k)Et,:?=Et+k,?(1) - 假定上面的公式是成立的,则存在
T
(
k
)
T^{(k)}
T(k):
T ( k ) = [ Φ 0 ( k ) 0 . . . 0 0 Φ 1 ( k ) . . . 0 0 0 ? 0 0 0 . . . Φ d m o d e l 2 ? 1 ( k ) ] \boldsymbol{T}^{(k)}=\boldsymbol{\left[\begin{array}{c} \boldsymbol{\Phi}_{0}^{(k)} \quad \bold{0} \quad ... \quad \bold{0}\\ \bold{0} \quad \boldsymbol{\Phi}_{1}^{(k)} \quad ... \quad \bold{0}\\ \bold{0} \quad \bold{0} \quad \ddots \quad \bold{0} \\ \bold{0} \quad \bold{0} \quad ... \quad \boldsymbol{\Phi}_{\frac{d_{model}}{2}-1}^{(k)}\\ \end{array}\right]} T(k)=??????Φ0(k)?0...00Φ1(k)?...000?000...Φ2dmodel???1(k)????????
其中, 0 \bold{0} 0表示 2 ? 2 2*2 2?2的全零矩阵,主对角线 d m o d e l 2 \frac{d_{model}}{2} 2dmodel??个元素可以表示为:
Φ m ( k ) = [ cos ? ( r m k ) ? sin ? ( r m k ) sin ? ( r m k ) cos ? ( r m k ) ] ? (2) \mathbf{\Phi}_{m}^{(k)}=\left[\begin{array}{cc} \cos \left(r_{m} k\right) & -\sin \left(r_{m} k\right) \\ \sin \left(r_{m} k\right) & \cos \left(r_{m} k\right) \end{array}\right]^{\top} \tag2 Φm(k)?=[cos(rm?k)sin(rm?k)??sin(rm?k)cos(rm?k)?]?(2)
带入公式(1)得到:
[ cos ? ( r m k ) sin ? ( r m k ) ? sin ? ( r m k ) cos ? ( r m k ) ] ? Φ m ( k ) [ sin ? ( λ m t ) cos ? ( λ m t ) ] = [ sin ? ( λ m ( t + k ) ) cos ? ( λ m ( t + k ) ) ] \underbrace{\left[\begin{array}{cc} \cos \left(r_{m} k\right) & \sin \left(r_{m} k\right) \\ -\sin \left(r_{m} k\right) & \cos \left(r_{m} k\right) \end{array}\right]}_{\Phi_{m}^{(k)}}\left[\begin{array}{l} \sin \left(\lambda_{m} t\right) \\ \cos \left(\lambda_{m} t\right) \end{array}\right]=\left[\begin{array}{l} \sin \left(\lambda_{m}(t+k)\right) \\ \cos \left(\lambda_{m}(t+k)\right) \end{array}\right] Φm(k)? [cos(rm?k)?sin(rm?k)?sin(rm?k)cos(rm?k)?]??[sin(λm?t)cos(λm?t)?]=[sin(λm?(t+k))cos(λm?(t+k))?]
对上式进行展开(点乘,忽略 m m m)为:
sin ? ( λ k + λ t ) = sin ? ( r k ) cos ? ( λ t ) + cos ? ( r k ) sin ? ( λ t ) cos ? ( λ k + λ t ) = cos ? ( r k ) cos ? ( λ t ) ? sin ? ( r k ) sin ? ( λ t ) (3) \begin{aligned} \sin (\lambda k+\lambda t) &=\sin (r k) \cos (\lambda t)+\cos (r k) \sin (\lambda t) \\ \cos (\lambda k+\lambda t) &=\cos (r k) \cos (\lambda t)-\sin (r k) \sin (\lambda t) \end{aligned} \tag3 sin(λk+λt)cos(λk+λt)?=sin(rk)cos(λt)+cos(rk)sin(λt)=cos(rk)cos(λt)?sin(rk)sin(λt)?(3)
另外,
s i n ( λ t + λ k ) = s i n ( λ t ) c o s ( λ k ) + c o s ( λ t ) s i n ( λ k ) c o s ( λ t + λ k ) = c o s ( λ t ) c o s ( λ k ) ? s i n ( λ t ) s i n ( λ k ) (4) \begin{aligned} sin(\lambda t+\lambda k)=sin(\lambda t)cos(\lambda k)+cos(\lambda t)sin(\lambda k) \\ cos(\lambda t+\lambda k)=cos(\lambda t)cos(\lambda k)-sin(\lambda t)sin(\lambda k) \end{aligned} \tag4 sin(λt+λk)=sin(λt)cos(λk)+cos(λt)sin(λk)cos(λt+λk)=cos(λt)cos(λk)?sin(λt)sin(λk)?(4)
综合公式(3)和公式(4)可以得到 r = λ r=\lambda r=λ,因此公式(2)可以表示为:
Φ m ( k ) = [ cos ? ( λ m k ) sin ? ( λ m k ) ? sin ? ( λ m k ) cos ? ( λ m k ) ] \mathbf{\Phi}_{m}^{(k)}=\left[\begin{array}{cc} \cos \left(\lambda_{m} k\right) & \sin \left(\lambda_{m} k\right) \\ -\sin \left(\lambda_{m} k\right) & \cos \left(\lambda_{m} k\right) \end{array}\right] Φm(k)?=[cos(λm?k)?sin(λm?k)?sin(λm?k)cos(λm?k)?]
其中 λ m = 1000 0 ? 2 m d m o d e l \lambda_{m}=10000^{\frac{-2m}{d_{model}}} λm?=10000dmodel??2m?。因此,通过上面的证明可以知道为什么选择正弦曲线函数,因为我们假设它能让模型很容易地学习关注相对位置,因为对于任何固定的偏移量k, P E p o s + k PE_{pos+k} PEpos+k?可以表示成 P E p o s PE_{pos} PEpos?的线性函数。
- 假定:
E
∈
R
n
×
d
model?
\boldsymbol{E} \in \mathbb{R}^{\boldsymbol{n} \times d_{\text {model }}}
E∈Rn×dmodel??表示行为n,列为
d
m
o
d
e
l
d_{model}
dmodel?的矩阵。则
E
E
E可定义为:
- 缺点:从上面的证明我们可以知道,函数式位置编码可以一定程度的表示相对位置信息,但是经过注意力层后,相对位置信息还保留多少?
- 在经过attention计算后,attention scores可表示为:
A i , j a b s = ( W q ( E x i + U i ) ) T ( W k ( E x j + U j ) ) (5) A_{i, j}^{a b s}=\left(W_{q}\left(E_{x_{i}}+U_{i}\right)\right)^{T}\left(W_{k}\left(E_{x_{j}}+U_{j}\right)\right) \tag5 Ai,jabs?=(Wq?(Exi??+Ui?))T(Wk?(Exj??+Uj?))(5)
其中, E x i , E x j E_{x_i},E_{x_j} Exi??,Exj??表示token embedding, U i , U j U_i,U_j Ui?,Uj?表示为position embedding。
经过展开后,可以得到:
A i , j a b s = E x i ? W q ? W k E x j ? ( a ) + E x i ? W q ? W k U j ? ( b ) + U i ? W q ? W k E x j ? ( c ) + U i ? W q ? W k U j ? ( d ) . (6) \begin{aligned} \mathbf{A}_{i, j}^{\mathrm{abs}} &=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(b)} \\ &+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(d)} . \end{aligned} \tag6 Ai,jabs??=(a) Exi???Wq??Wk?Exj????+(b) Exi???Wq??Wk?Uj???+(c) Ui??Wq??Wk?Exj????+(d) Ui??Wq??Wk?Uj???.?(6)
公式(6)中,a与位置编码无关,b,c只包含单个token的位置编码,所以跟相对位置编码有关的只有d。 - 如果在公式(6)中,d项没有
W
q
T
W
k
W^T_qW_k
WqT?Wk?,
U
i
T
U
j
U^T_iU_j
UiT?Uj?是可以表示相对位置信息的。
- 证明:
如果: P E t = [ sin ? ( c 0 t ) cos ? ( c 0 t ) ? sin ? ( c d 2 ? 1 t ) cos ? ( c d 2 ? 1 t ) ] P E_{t}=\left[\begin{array}{c} \sin \left(c_{0} t\right) \\ \cos \left(c_{0} t\right) \\ \vdots \\ \sin \left(c_{\frac{d}{2}-1} t\right) \\ \cos \left(c_{\frac{d}{2}-1} t\right) \end{array}\right] PEt?=??????????sin(c0?t)cos(c0?t)?sin(c2d??1?t)cos(c2d??1?t)???????????
则:
P E t T P E t + k = ∑ j = 0 d 2 ? 1 [ sin ? ( c j t ) sin ? ( c j ( t + k ) ) + cos ? ( c j t ) cos ? ( c j ( t + k ) ) ] = ∑ j = 0 d 2 ? 1 cos ? ( c j ( t ? ( t + k ) ) ) = ∑ j = 0 d 2 ? 1 cos ? ( c j k ) \begin{aligned} P E_{t}^{T} P E_{t+k}=& \sum_{j=0}^{\frac{d}{2}-1}\left[\sin \left(c_{j} t\right) \sin \left(c_{j}(t+k)\right)\right.\\ &\left.\quad+\cos \left(c_{j} t\right) \cos \left(c_{j}(t+k)\right)\right] \\ =& \sum_{j=0}^{\frac{d}{2}-1} \cos \left(c_{j}(t-(t+k))\right) \\ =& \sum_{j=0}^{\frac{d}{2}-1} \cos \left(c_{j} k\right) \end{aligned} PEtT?PEt+k?===?j=0∑2d??1?[sin(cj?t)sin(cj?(t+k))+cos(cj?t)cos(cj?(t+k))]j=0∑2d??1?cos(cj?(t?(t+k)))j=0∑2d??1?cos(cj?k)? - 图示如下:
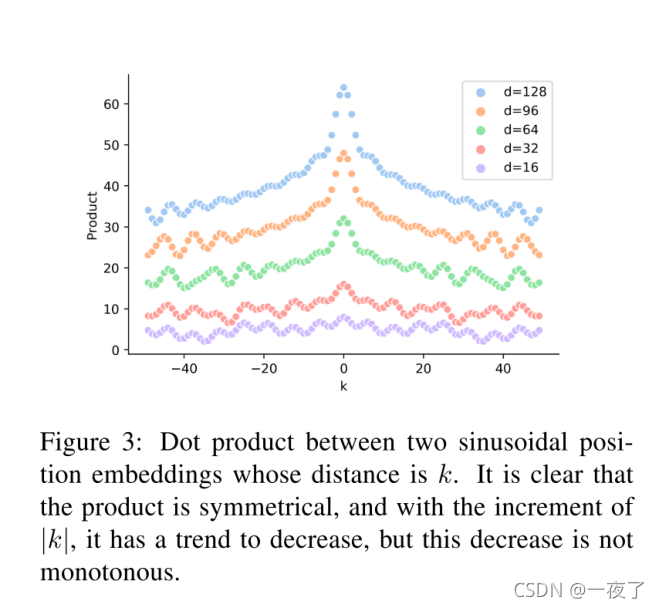
- 证明:
- 在经过attention计算后,attention scores可表示为:
从图中可以看出,这种表示是能够表示位置信息的,但是却不能表示方向。
* 如果加上
W
q
T
W
k
W^T_qW_k
WqT?Wk?,
W
q
T
W
k
W^T_qW_k
WqT?Wk?随机初始化的话可以得到:
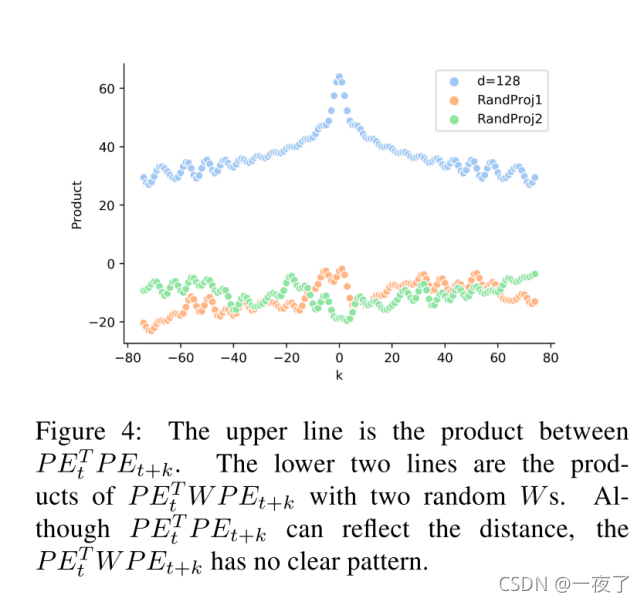
从图中,可以看出这种方式在模型训练初期是不能够很好的表示距离的,但是如果随着模型的训练,这种方式有可能会表示好的位置信息。但是,至少在模型训练的初期,模型并不能很好的学习位置信息,从而会增加模型训练的难度和时间,一定程度上,也会对位置信息学习不够完整。
再续
针对上面提到的位置编码该怎么优化?有哪些方法?参见系列文章《位置编码 - 领略位置编码神奇的风景 - 系列(2)》
