前言

应闵老师要求，在开学前阅读完，然后讲解出来。

一、多标签主动学习？

图像分类是对图像进行标注，以描述图像的语义信息

多标签图像分类的成功与否与构建训练集的方式密切相关。由于主动学习旨在通过迭代地选择信息量最大的示例来构建有效的训练集以从注释器中查询标签，因此将其引入多标签图像分类。
该综述将目前多标签图像分类算法分别从两个方面分为两大类:采样和注释（注释还不清楚在是什么，有什么用，在一个具体的数据集中值哪部分？）。
多标签主动学习的最重要组成部分是设计一种有效的采样策略，根据各种信息度量，从未标记的数据池中主动选择信息量最高的示例。因此，本次调查强调了不同的信息量衡量标椎
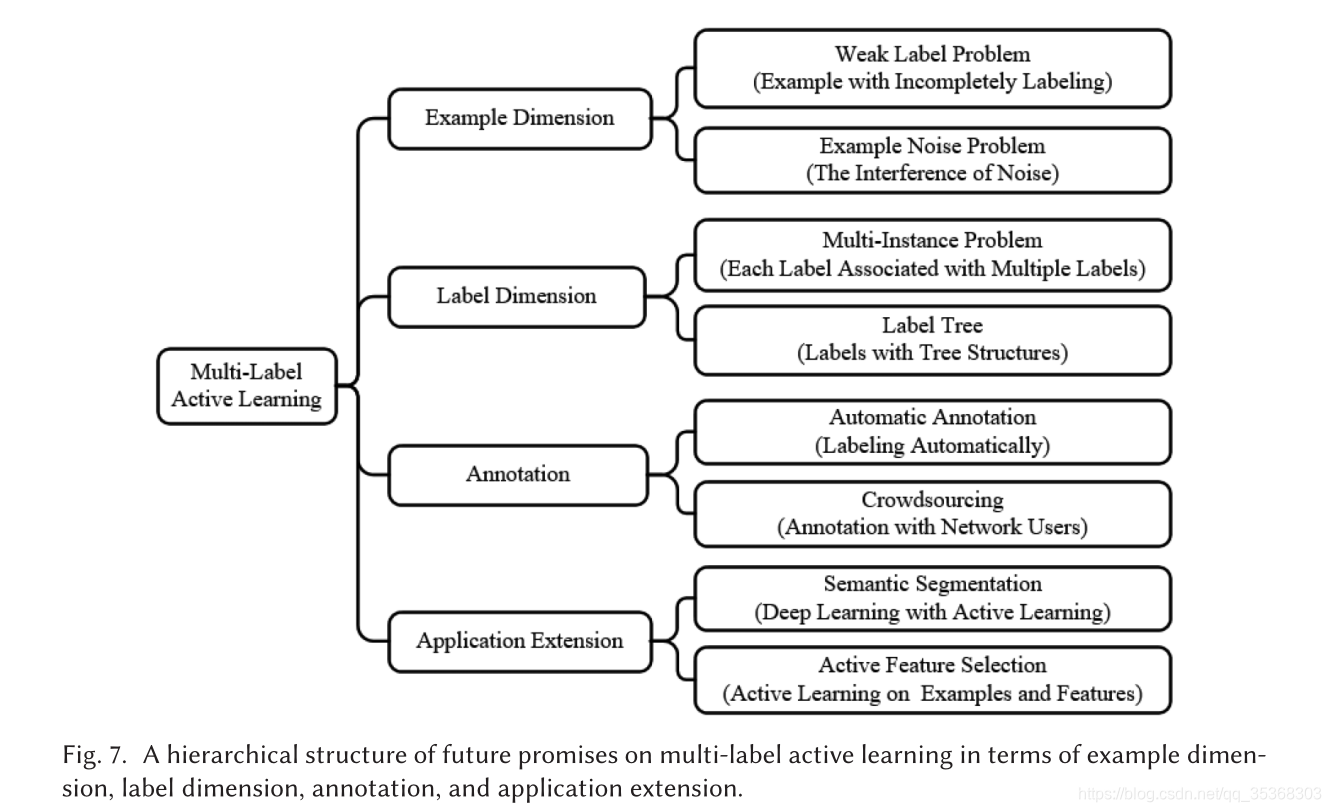
该文阐述多标签主动学习重点关注四个核心方面：示例维度、标签维度、注释和应用程序扩展。

1.为什么选择主动学习进行多标签图像分类

为了充分利用未标记图像，提出了两种主要的机器学习方法，即半监督学习和主动学习。根本区别是在训练过程中是否需要专家对图像进行额外的标记。
主动学习需要从领域专家那里获取一些未标注图像的标签，从而保证标注的准确性。在资源有限的情况下，主动学习迭代地选择信息量最大的例子来获取它们的标签，并从更新后的训练集中训练分类器，然后用新选择的例子扩充训练集。主动学习不仅大大减少了标注工作量，而且为高性能分类器的训练构建了有效的训练集。

二、多标签主动学习问题定义，并解释其总体框架

根据不同的查询方式，主动学习算法分为三种：成员查询合成主动学习，基于流的选择性主动学习，基于池的主动学习。
本文着重对基于池的主动学习进行分析和讨论。
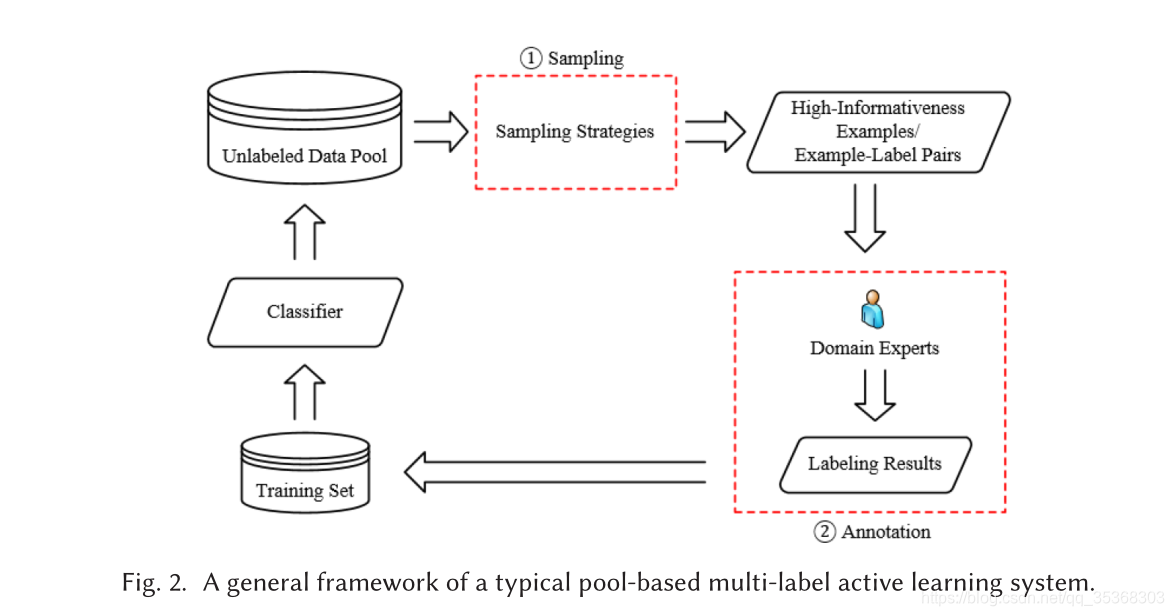
在这里插入图片描述
Given a multi-label active learning problem, there is an example set $X=\left\{x_{1}, \ldots, x_{n}\right\}$ consisting of $n$ examples. Each example $x_{i}$ belongs to a $d$ -dimensional feature space and is associated with the possible label set $Y_{i}$ , where $Y_{i}$ is a subset of the total label set $A=\left\{l_{1}, l_{2}, \ldots, l_{n_{m}}\right\}$ and $n_{m}$ is the number of labels in $A$ .
此外，给出了多标签实例、示例-标签对和信息量的定义如下。

Definition 1. Multi-label example: A multi-label example $x_{i}$ can be denoted as $\left\{x_{i}, Y_{i}\right\}$ , where $x_{i}=\left\{v_{1}^{i}, v_{2}^{i}, \ldots, v_{d}^{i}\right\}$ , and $v_{d}^{i}$ denotes the $d$ th feature value of $x_{i} . Y_{i}=\left\{y_{i, l_{1}}, y_{i, l_{2}}, \ldots, y_{i, l_{n_{m}}}\right\}$ denotes the label set of $x_{i}$ .

Definition 2. Example-label pair: An example-label pair can be denoted as $\left(x_{i}, y_{i, l_{s}}\right)$ , where $x_{i}=\left\{v_{1}^{i}, v_{2}^{i}, \ldots, v_{d}^{i}\right\}$ , and $y_{i, l_{s}}$ denotes the sth label of $x_{i}$ and $y_{i, l_{s}} \in\{0,1\}$ is contained in the label set $Y_{i}$ of example $x_{i} \cdot y_{i, l_{s}}=0$ indicates that the label $y_{i, l_{s}}$ does not belong to the example $x_{i} \cdot y_{i, l_{s}}=1$ indicates that the label $y_{i, l_{s}}$ belongs to the example $x_{i}$ .

Definition 3. Informativeness: The measurement of useful information of an unlabeled example $x_{i}$ or example-label pair $\left(x_{i}, y_{i, l_{s}}\right)$ .

In a typical multi-label active learning scenario, there is an example set $X$ including a small labeled training set $L=\left\{\left(x_{i}, Y_{i}\right) \mid 1 \leq i \leq n_{l}\right\}$ and a large unlabeled dataset $U=\left\{\left(x_{j}, Y_{j}\right) \mid 1 \leq j \leq\right.$ $\left.n_{u}\right\}$ . Here, $n_{l}$ is the number of examples in $L$ , and $n_{u}$ is the number of examples in $U\left(n_{l} \ll n_{u}\right) .$ 它的最终目标是学习高性能的多标签分类器 $\Theta: X \rightarrow A$ . 伪代码展示为算法 $1 .$
在这里插入图片描述

三、目前常用方法

多标签主动学习算法的层次结构图：
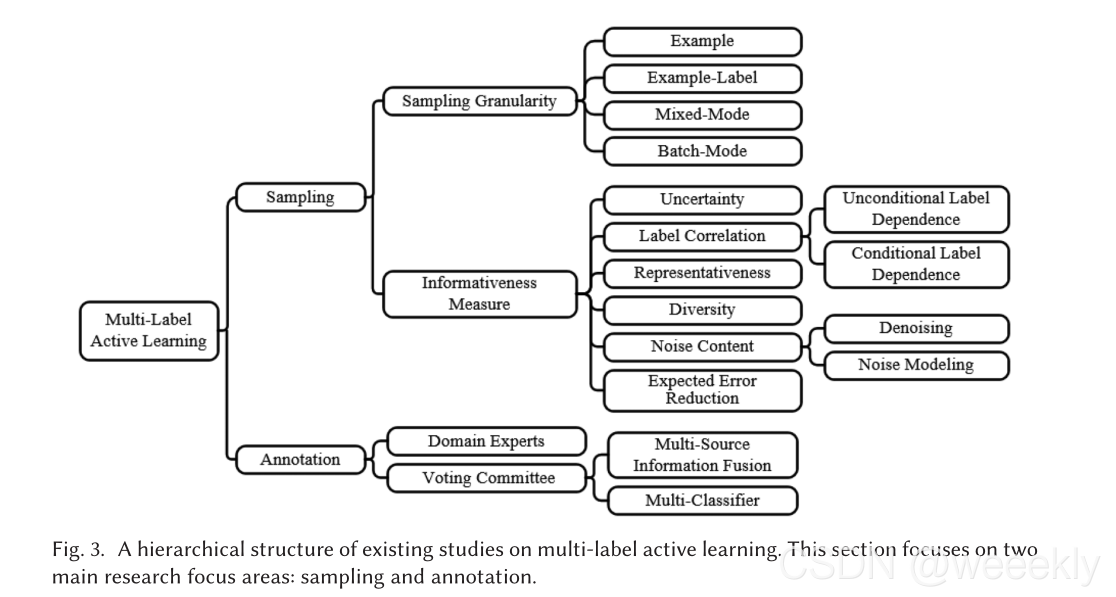
在这里插入图片描述

3.1 采样策略

3.1.1抽样粒度

1.1.1基于示例的方法:
方法定义：
通过信息型度量函数 $\operatorname{In}fo(\cdot)$ ，选择信息性大的未标注实例，然后对每个实例 $x$ ，从领域专家处获取所有标签。
$x^{*}=\underset{x_{j} \in U}{\arg \max } \operatorname{In} f o\left(x_{j}\right)$ $U 表示未标记的数据池$

信息量可以从几个方面进行评估，由于不同的信息度量对模型训练的影响是不同的，因此使用权衡参数来平衡这些度量的相对重要性。因此，一个未标记例子的信息性度量函数 $\operatorname{In}fo(\cdot)$ 可以表示为:
$\begin{aligned} &\operatorname{Info}\left(x_{j}\right)=\sum \alpha_{s} I_{s}\left(x_{j}\right) \\ &\text { s.t. } \alpha_{s} \in[0,1], \sum \alpha_{s}=1 \end{aligned}$
$I_{s}\left(x_{j}\right) 是信息测量方法之一, \alpha_{s} 是第s个权衡参数$
提出了将多标签分类问题分解为一组二值分类问题来解决多标签场景分类问题，并建立了多标签场景分类框架。
参数设置：
一是根据经验和约束条件设定固定的参数。选择模型所使用的分类性能最高的参数组作为最终参数设置。
另一种方法是开发自适应参数调优方案（解释： $n_m$ 表示 $\alpha$ 取值的个数，然后 $n_m$ 个 $f$ 组成一个多标签分类器 $\Theta$ ,通过分类器测出 $x^{'}$ 的标签集 $Y^{'}$ ,然后将该实例加入实例集合 $L$ ,训练出新的多标签分类器）
在这里插入图片描述

1.1.2基于示例标签的方法

1.1.3基于混合模式的方法

1.1.4基于批处理模式的方法

3.1.2信息度量

如前所述，采样策略是多标签主动学习算法的关键，其目标是对信息量高的示例/示例-标签对进行标注。
抽样策略的核心是对每个样本的信息性进行评估的信息度量。
现有的多标签主动学习算法中使用的不同基本信息度量。将这些基本的信息量指标分为六组。
(1)不确定性度量;
不确定抽样的目的是选择当前分类器预测中最不确定的一个示例/示例标签对，这是一种简单而广泛使用的策略。
(训练几个SVM分类器，同时计算了一个示例中所有标签的SVM裕度值。通过将边缘概率转化为概率分数，所有支持向量机的平均概率可以识别示例的不确定性。)
标签的边距值： $\operatorname{mar}_{j}\left(y_{j, k}\right)=\left|p\left(y_{j, k}=1 \mid x_{j}\right)-p\left(y_{j, k}=0 \mid x_{j}\right)\right|$
通过上式, 得到了一个边际值向量 $M\left(x_{j}\right)=\left[\operatorname{mar}_{j}\left(y_{j, 1}\right), \ldots\right.$ , $\left.\operatorname{mar}_{j}\left(y_{j, n_{m}}\right)\right]$ 对于每个未标记的例子 $x_{j} .$ 然后，收集并列出标签上所有未标记示例的边距值 $y_{j, k}$ , 计算了一个排名 $\tau_{y_{j, k}}$ 将未标记的示例排序如下:
$\tau_{y_{j, k}}=\left(x_{1}, x_{2}, \ldots, x_{n_{u}}\right) \mid \operatorname{mar}_{1}\left(y_{j, k}\right)<\cdots<\operatorname{mar}_{n_{u}}\left(y_{j, k}\right)$
之后，他们采用了Borda的方法，这是一种定位方法，根据元素在每个排名中出现的位置给元素赋值，计算每个未标记示例 $x_{j}$ 的分数如下：
$c\left(x_{j}\right)=\frac{\sum_{y_{j, k} \in Y_{j}}\left(n_{u}-\tau_{y_{j, k}}\left(x_{j}\right)\right)}{n_{m}\left(n_{u}-1\right)}$
使用最简单和最广泛的方法可以记为:
$\operatorname{Unc}\left(x_{j}, y_{j, k}\right)=\left|\frac{1}{2}-p\left(y_{j, k}=1 \mid x_{j}\right)\right|,$
(2)标签相关度量;
(3)代表性指标;
(4)多样性度量;
(5)噪声含量度量;
(6)期望误差减少度量

3.2标注算法

手动和自动注释
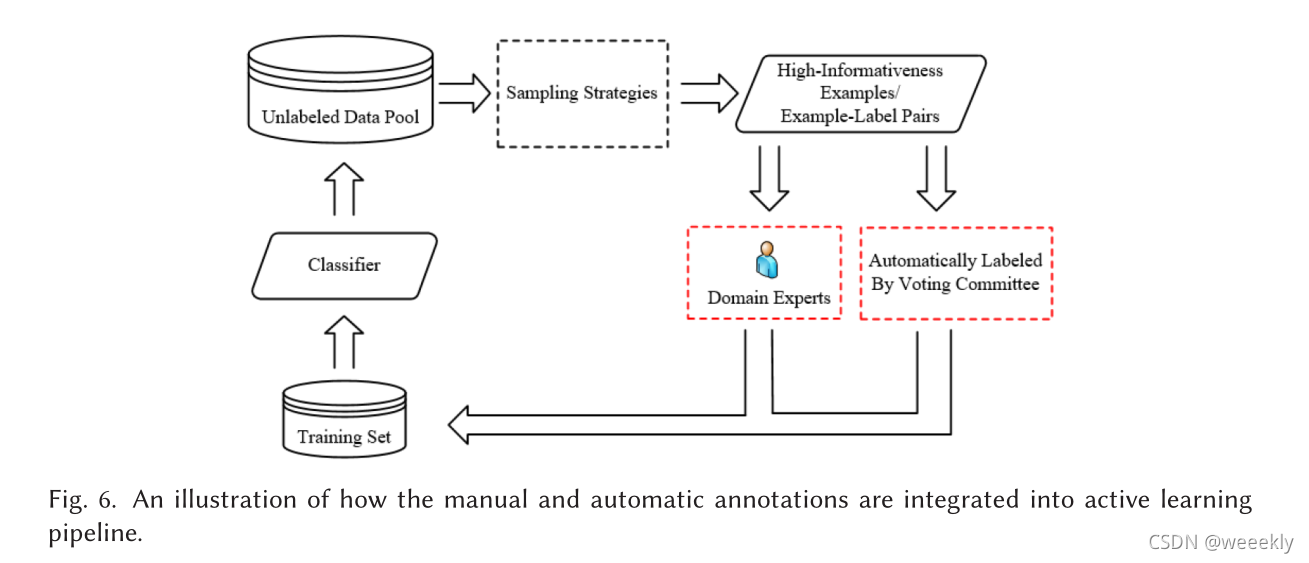
在这里插入图片描述
由于领域专家成本高，标注工作量大，领域专家难以处理，因此许多多标签主动学习研究采用自动标注，可以大大降低标注成本。我们可以从图 6 中通过投票委员会了解自动注释的过程。具体而言，在投票委员会方法的每次迭代中，通过选择策略选择的候选示例/示例-标签对按照分配标准分为两部分。候选示例/示例-标签对的一部分由领域专家标记作为自动注释的辅助工具，而另一部分由投票委员会自动标记。分配标准和构建投票委员会的方法是自动注释的主要组成部分。后者非常重要。根据不同的建模方法，现有的构建投票委员会的方法分为两类：基于多源信息融合的和基于多分类器的。