一、简介
一、社区的定义
? Newman第一次提出模块度定义就是在2004年发表的这篇文章“fast algorithm for community structure in networks”,第一次用量化的公式来确定社区划分。
? 首先,我们来看Newman如何定义社区的:the vertices in networks are often found to cluster into tightly knit groups with a high density of within-group edges and a lower density of between -group edges。
? 用大白话说就是:社区内部的边尽可能地多,但是社区之间的边尽可能地少
(一些定义):i、j指社区i和社区j;
? n是网络中节点的数量;
? m是网络中边的数量。一条边上连接两个节点,和明显,2m即网络中所有节点度之和
二、如何量化到模快度?
? 我们先用eij表示社区i和社区j之间连接的边的数量比整个网络边的数量,eii表示社区i内部边的数量比整个网络边的数量,既然这样的话我们只要使∑ieii尽可能大就好了,但是问题又来了,最大肯定就是1咯,所有节点归为一个社区,那这样很明显就没有意义了。
? 于是他有提出,网络中连接两个同种类型的边(即社区内部的边的比例eii)减去在相同结构下任意连接这两个节点边的比例的期望,于是模块度登场
? Q=∑i(eii-ai2)
其中,ai=∑jeij 表示与社区i中节点相连的边占所有边的比例。如果社团内部边的比例不大于社团内部边随机连接的期望,那么Q=0,最大时为1。一般来说,Q值最大对应的社团结构就是网络中的社团结构
三、如何变成算法可操作性?
? 意思来了,我们只要优化Q就好了,但是如何把n个节点划分多少个社区?每个社区多少个节点?作者指出有2n-1种可能,这样的话根本无法将Q推广在高于20节点以上的网络?为了减少时间复杂度,作者提出一种贪婪策略
? FN:(1)首先将网络中每个节点自定义成一个社区
? (2)计算出两两社区结合是Q的值,找到Q增加最大的或者减少最少的合并方式进行社区合并
? (3)直到所有社区合并成一个大社区时停止,找出合并过程中最大的Q是的社区划分结果
这个时候,Newman有注意到,当两个社区合并时,模块度的增量detaQ=(eji+eij-2aiaj)=2(eij-2aiaj)
二、代码
clear;clc
load('50.mat')
% 生成adjacent_matrix矩阵
adjacent_matrix = link;
[Z, Q_all] = FastNewman(adjacent_matrix);
class_count = 4; % 最大的模块都对应的类个数
class_cell = class_cal(Z, class_count); % 分类情况
% 聚类画图
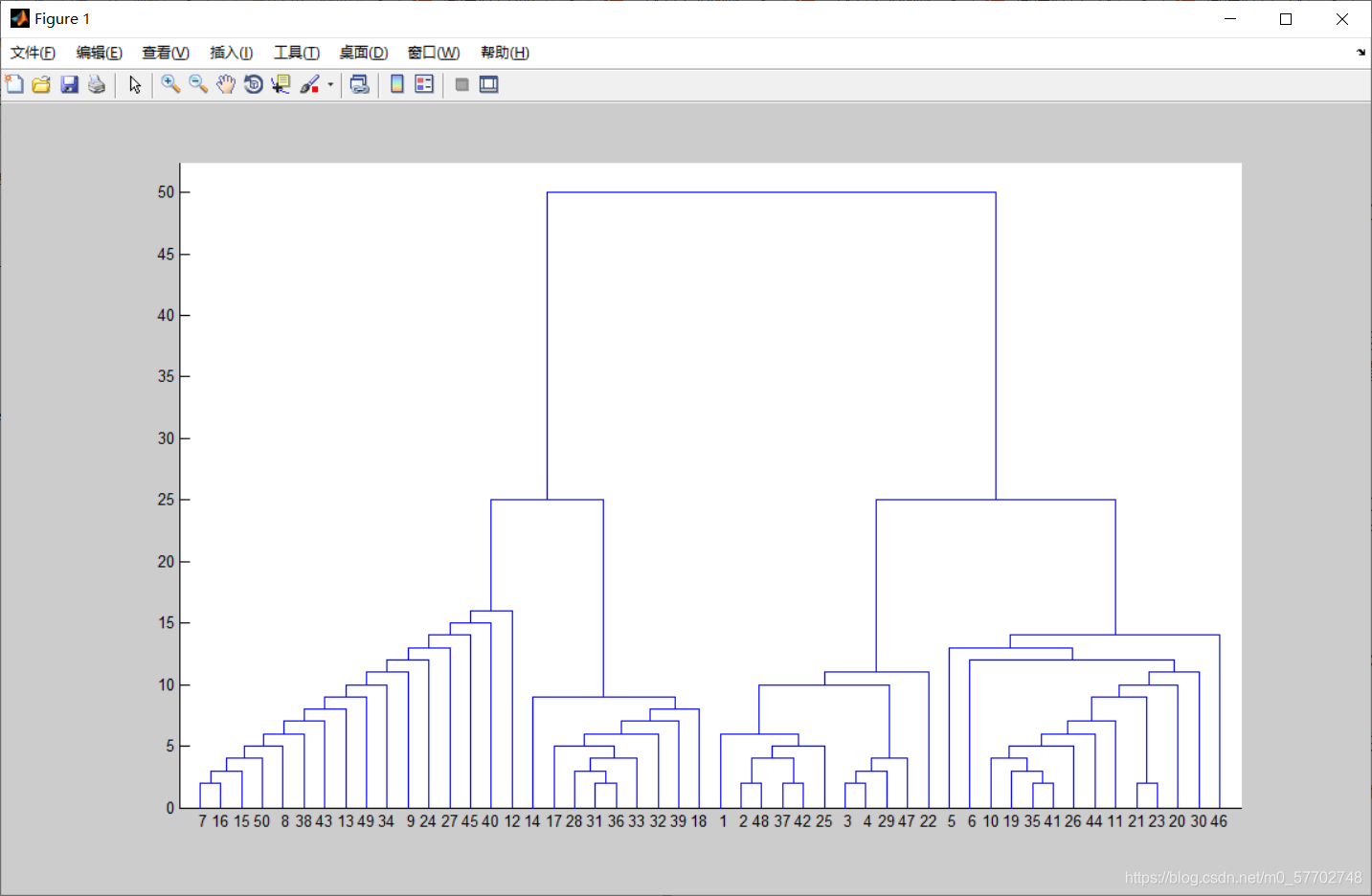
figure(1)
H = dendrogram(Z,0);
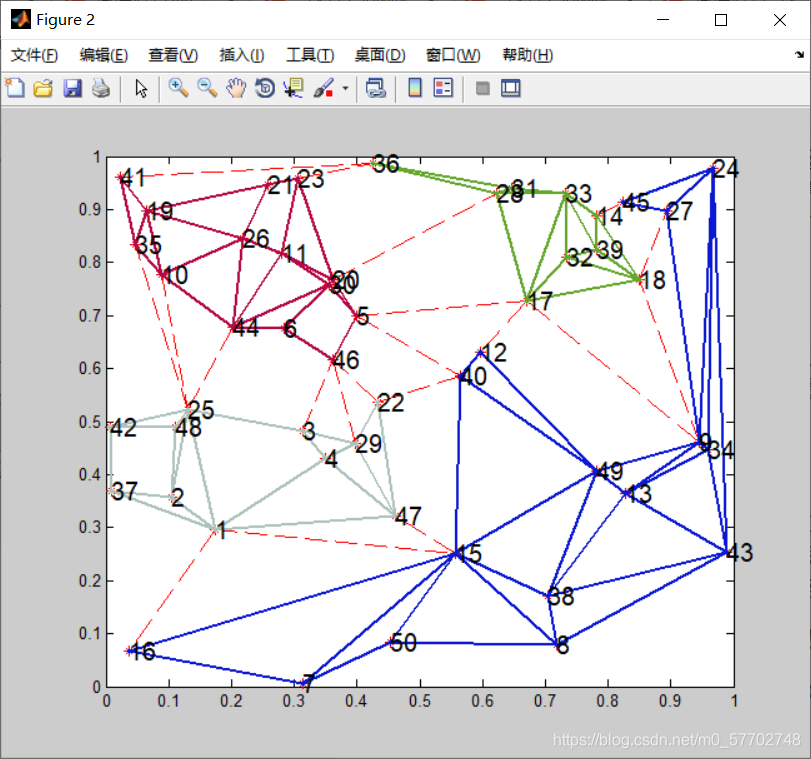
figure(2)
plot(node(:,1), node(:,2), 'r*')
hold on
for i = 1:size(link, 1)
plot(node(link(i,:), 1), node(link(i,:), 2), 'r--')
end
for i = 1:length(class_cell)
c = [rand rand rand];
for j = 1:size(link, 1)
if all(ismember(link(j,:), class_cell{i}))
plot(node(link(j,:), 1), node(link(j,:), 2), '.-', 'linewidth', 2, 'color', c)
end
end
end
for i = 1:size(node,1)
text(node(i,1), node(i,2), num2str(i), 'fontsize', 15, 'color', 'k')
end
?