[人工智能]PCA（主成分分析）降维算法

当数据特征较多时，为方便运算和简化分析，我们能不能从中提取有效信息，把原数据用更低维数据表示？

假设现在有n个样本，有如下的二维数据：
[x1, y1 ; x2, y2 ; … ;xn, yn]
先将数据规范化（中心化），即均将所有点的横坐标均值与纵坐标均值变成0，处理方法为每个点的横坐标减去所有点横坐标均值，纵坐标同理。
在主成分分析中，若有一低维平面能有效提取原数据信息，则它应一般满足最大可分性：样本点在这一低维平面的投影尽可能分开，也就是方差最大原则。
从下面图片就能看出，主成分最好选择Component 1，这时数据在Component 1上的投影较Component 2上方差明显大。

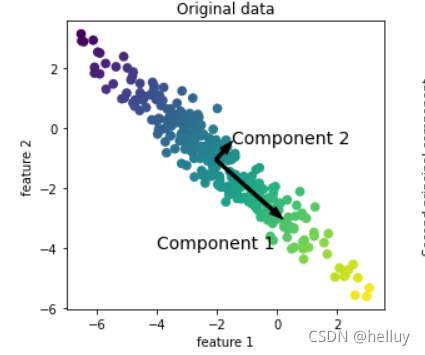
那如何确定主成分，确定后如何选择主成分？下面进行简单算法推导。
我们将原数据写成矩阵的形式如下：
$$A=?\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\\ ...& ...\\ x_n& y_n\end{array}?\text{\hspace{1em}(3)}$$
其中 $\overline{x}=0，\overline{y}=0$，则
横坐标方差$S^2(x)=\frac{\sum _{i=1}^n{x}_i^2}{n?1}$
纵坐标方差$S^2(y)=\frac{\sum _{i=1}^n{y}_i^2}{n?1}$
协方差为$cov(x,y)=\frac{\sum _{i=1}^n{x}_i{y}_i}{n?1}$
协方差矩阵为：$$C=\left[\begin{array}{cc}{S}^2(x)& cov(x,y)\\ cov(x,y)& S^2(y)\end{array}\right]=\frac{A^{T}A}{n?1}\text{\hspace{1em}(3)}$$
现定义一单位向量$u$，求各样本点所表示向量在$u$方向上投影的长度，使长度方差最大。
设一样本对应向量为$a$，即其在$u$上投影长度表示为两向量的点乘：$$a?u=|a||u|cos\theta =|a|cos\theta$$
设，每个样本在$u$上的投影长度为$s_i$，因为数据为中心化的数据， 所以长度的方差为
$$S^2=\frac{\sum _{i=1}^n{s}_i^2}{n?1}=\frac{u{A}^T?(u{A}^T{)}^T}{n?1}=u\frac{A^{T}A}{n?1}{u}^T=uC{u}^T$$
所以我们的目标转化为使$S^2$即$uC{u}^T$最大。
现利用拉氏函数求目标函数$J$的最大值。
目标函数:$$J=S^2=uC{u}^T$$
约束条件:$$u{u}^T=1$$
拉氏函数:$$F(u)=uC{u}^T?\lambda (1?u{u}^T)$$
对$u$求偏导:
$$\frac{{?}^{}F}{?u^{}}=0?C{u}^T=\lambda u^T$$
此时$C$已知，为协方差矩阵，$u，\lambda$分别为$C$的特征向量、特征值，可以求出。
此时$A{u}^T$代表原二维坐标平面在一维向量$u$上的投影，或者是在以$u$方向轴上的坐标，形状为nx1，此时$A{u}^T$就可以作为原数据的一个主成分。
但此时根据$C$可以求出两个不同的特征向量，方向分别对应Component 1，Component 2。如何选取？
答：看$S^2$，也就是在特征向量方向轴上的投影长度方差，方差越大，可以认为，含有原数据信息量越全面。
前面提到长度的方差$S^2=uC{u}^T$，而由拉式函数偏导结果$$C{u}^T=\lambda u^T$$带进$S^2$，得到$$S^2=\lambda$$，即原数据在对应特征向量方向轴上的方差就是该特征向量对应的特征值!!!
可以看出，特征值越大，方差越大，对原数据的信息保留越全面。
第i主成分覆盖信息率为$$\frac{{\lambda }_i}{{\lambda }_1+{\lambda }_2+...+{\lambda }_n}$$
我们应选取覆盖信息率高的主成分作为原数据的主成分，主成分为$A{u}^T$。