什么是奇异值分解
SVD是一种矩阵分解算法,在某些情况下,矩阵具有特定的结构,如果矩阵中有规则或简单的结构,那么分解矩阵将是有意义的。先看以下几个例子:
例子1.以下是一个所有元素值都相等的矩阵
A
=
(
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
)
A=\begin{pmatrix} 1 &1 &1 &1 &1 &1 \\ 1 &1 &1 &1 &1 & 1\\ 1 &1 &1 &1 &1 &1 \\ 1 &1 &1 &1 &1 &1 \\ 1 &1 &1 &1 &1 &1 \\ 1 &1 &1 &1 &1 &1 \end{pmatrix}
A=?????????111111?111111?111111?111111?111111?111111??????????
如果要保存这个矩阵,通常可以压缩这个矩阵,压缩的方法有很多,此时如果用向量积的方式实现,如下所示:
A
=
(
1
1
1
1
1
1
)
(
1
1
1
1
1
1
)
A=\begin{pmatrix} 1\\ 1\\ 1\\ 1\\ 1\\ 1 \end{pmatrix}\begin{pmatrix} 1 &1 &1 &1 &1 &1 \end{pmatrix}
A=?????????111111??????????(1?1?1?1?1?1?)
此时只需保存12个元素,而不是36个元素
例子2.意大利国旗

意大利国旗可以写成以下矩阵形式:
A
=
(
g
g
w
w
r
r
g
g
w
w
r
r
g
g
w
w
r
r
g
g
w
w
r
r
g
g
w
w
r
r
g
g
w
w
r
r
)
A=\begin{pmatrix} g &g &w &w &r &r \\ g &g &w &w &r &r \\ g &g &w &w &r &r \\ g &g &w &w &r &r \\ g &g &w &w &r &r \\ g &g &w &w &r &r \end{pmatrix}
A=?????????gggggg?gggggg?wwwwww?wwwwww?rrrrrr?rrrrrr??????????
同样的,也能用一种非常好的方式来压缩它,如下:
A
=
(
1
1
1
1
1
1
)
(
g
g
w
w
r
r
)
A=\begin{pmatrix} 1\\ 1\\ 1\\ 1\\ 1\\ 1 \end{pmatrix}\begin{pmatrix} g & g & w &w &r &r \end{pmatrix}
A=?????????111111??????????(g?g?w?w?r?r?)
例子3:现有如下矩阵A
A
=
(
1
0
1
1
)
A=\begin{pmatrix} 1 &0 \\ 1 &1 \end{pmatrix}
A=(11?01?)
分解这样的矩阵可以考虑用以上的方法,显然,不能只用一对行列向量完成分解。可以考虑将矩阵分解为两项的和(差),如下:
A
=
(
1
1
)
(
1
1
)
?
(
1
0
)
(
0
1
)
A=\begin{pmatrix} 1\\ 1 \end{pmatrix}\begin{pmatrix} 1 &1 \end{pmatrix}-\begin{pmatrix} 1\\ 0 \end{pmatrix}\begin{pmatrix} 0 &1 \end{pmatrix}
A=(11?)(1?1?)?(10?)(0?1?)
那么奇异值分解实际上在做什么?
SVD将矩阵分解为一组向量v(可以看成多个列向量)、一组向量u(可以看成多个行向量)和一个对角矩阵(可以看成多个标量),即将矩阵分解为多项式。
如果有一个秩r=2的矩阵,我们可以将矩阵分解为
u
1
v
1
T
+
u
2
v
2
T
u_{1}v_{1}^{T}+u_{2}v_{2}^{T}
u1?v1T?+u2?v2T?
如果有一个秩r=1的矩阵,结果如下
u
1
v
1
T
u_{1}v_{1}^{T}
u1?v1T?
稍微复杂一点的分解是添加标量\alpha存储在对角矩阵中,对于秩r=2的矩阵,分解结果如下
σ
1
u
1
v
1
T
+
σ
2
u
2
v
2
T
\sigma _{1}u_{1}v_{1}^{T}+\sigma _{2}u_{2}v_{2}^{T}
σ1?u1?v1T?+σ2?u2?v2T?
显然,sigma值可以认为是加权系数。
SVD的特征向量
从以上例子可以看出,任何矩阵都可以分解为向量u和向量v,现在需要思考的是矩阵是如何分解的,SVD的思想如下:
A
=
U
Σ
V
T
A=U\Sigma V^{T}
A=UΣVT
- 向量U为左奇异向量,它是AA^T的单位向量
- 向量V为右奇异向量,它是A^TA的单位向量
- sigma为奇异值(\Sigma 对角线上的元素),它是AA^T的特征值的平方根
通过以下公式计算特征向量U:
A
A
T
u
i
=
σ
i
2
u
i
AA^{T}u_{i}=\sigma _{i}^{2}u_{i}
AATui?=σi2?ui?
SVD定义
由上节可知,SVD分解会得到一组新的矩阵,如果将它们相乘的话,将得到原始矩阵。奇异值分解的思想是将这个矩阵分解为三项的乘积,这三项分别为矩阵U、、V。
A
=
(
?
?
?
?
a
1
a
2
?
a
m
?
?
?
?
)
=
U
Σ
V
T
A=\begin{pmatrix} \vdots &\vdots &\vdots &\vdots \\ a_{1}&a_{2} & \cdots &a_{m} \\ \vdots &\vdots &\vdots &\vdots \end{pmatrix}=U\Sigma V^{T}
A=??????a1????a2????????am????????=UΣVT
矩阵A是m列向量,长度为n,即A的维度为mxn,
矩阵U的维度为nxn,
矩阵V的维度为mxm,
矩阵D的维度为nxm
d
i
m
{
A
}
=
n
×
m
d
i
m
{
U
}
=
n
×
n
d
i
m
{
Σ
}
=
n
×
m
d
i
m
{
V
}
=
m
×
m
dim\left \{ A \right \}=n\times m\\ dim\left \{ U \right \}=n\times n\\ dim\left \{ \Sigma \right \}=n\times m \\ dim\left \{ V \right \}=m\times m
dim{A}=n×mdim{U}=n×ndim{Σ}=n×mdim{V}=m×m
用图像进行解释说明,矩阵A可以认为将图像进行矢量化并存储为列,矩阵U可以认为与A中的列对应的相似列。与特征向量类似,我们将这些“向量面”成为特征面,用特征面来表示人脸,这是图像处理和计算机视觉中用于人脸分析的基本方法。
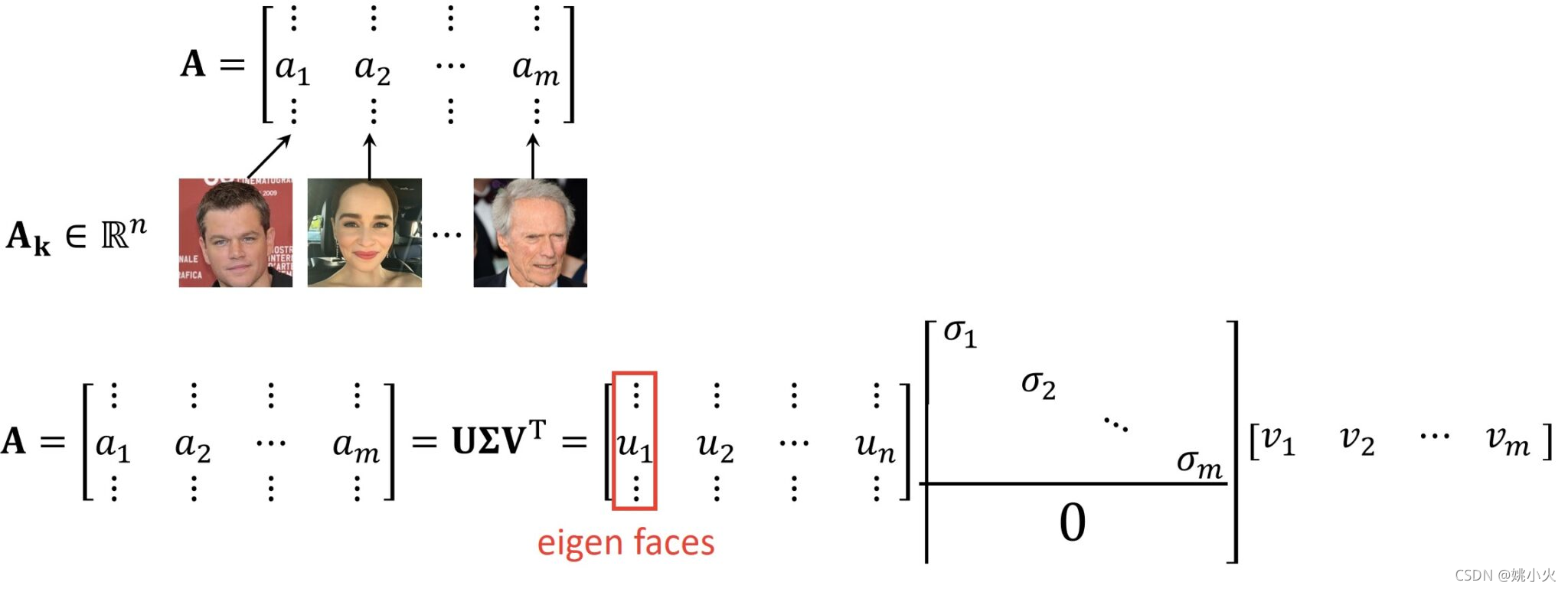
矩阵U和V为实对称矩阵,即将U和UT相乘、V和VT相乘,得到的是单位矩阵。
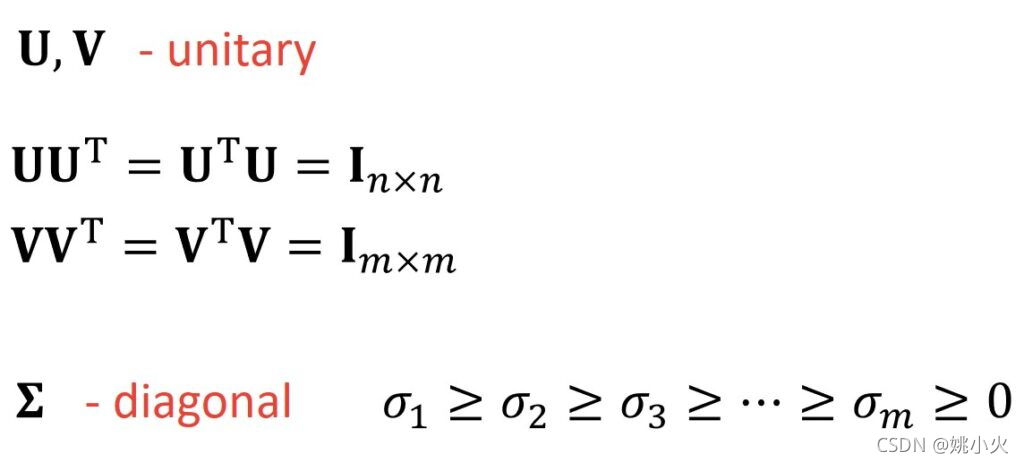
因此,
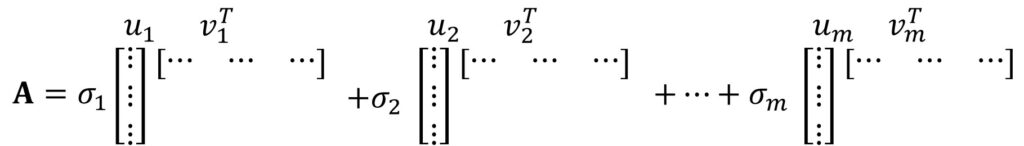
应用
输入一张人脸图像
faces = X[0,:].reshape((64,64))
通过奇异值进行分解
# we decompose the image of a face
U, S, VT = np.linalg.svd(faces)
S = np.diag(S)
faces = faces.astype('float')
#U, VT = truncate_u_v(S, U, VT)
draw_svd(faces, U, S, VT, 'gray')
输出为:

可以求出前30个特征值
diag_elem = np.diag(S)
plt.stem(diag_elem[1:])
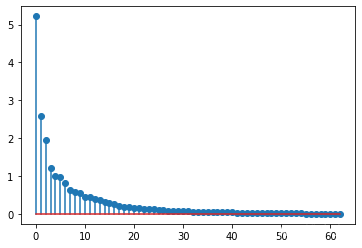
当然,这里可以取前n个特征值进行重建,剩下的特征值舍弃,显然,取得的特征值越多,图像的轮廓越清晰。因为越靠前的特征值和特征向量,权重越大,越靠后,权重越小。
ps:如果矩阵A为mxn,用奇异值分解,如果A是方阵,用特征值分解即可。