[人工智能]2.2.线性分类器——softmax

1.Softmax损失函数和梯度求导

1.1.理论推导

参考：CS231n课程学习笔记（三）——Softmax分类器的实现

? 对于某张图片Xi来说，损失函数的定义：

? 对于求导来说，需要用到链式法则，即

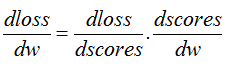
? 对于某张图片数据Xi，由于Scores = W * x，所以对W求导比较简单，结果就是x.T，注意这里最好严谨一点写成x.T，而不是x。

? 而loss对score的求导，由于fj或者fyi分别在分母或者分子上，也就是并不同在分子或者分母上，所以需要分开求导。

• $j!=y_i$ 此时是对非正确项的分母的各个fj求导：

  

• $j==y_i$ 此时是对正确项的分字$f{y}_i$求导：

? 最后的结果如下：

• 思考总结：到这里可以发现规律，就是求导的结果都是$dW=x.T?margin$，这个margin就是由得分函数来确定的，比如得分函数是SVM或者Softmax，具体margin的形式可以由公式先推导一张图片数据xi的形式，然后得到的公式对应的就是margin中的某一行的数据表达方式。并且这个margin正确类别和不正确类别的表达是有区别的，对应就是margin中正确类别所在的位置的数据和其他位置的数据是不一样的。

• 另外网上看到的另一个softmax求导的计算，写的比较简介规范：

  

1.2.编程实现

1.2.1.循环模式

def softmax_loss_naive(W, X, y, reg):
    """
    Softmax loss function, naive implementation (with loops)

    Inputs have dimension D, there are C classes, and we operate on minibatches
    of N examples.

    Inputs:
    - W: A numpy array of shape (D, C) containing weights.
    - X: A numpy array of shape (N, D) containing a minibatch of data.
    - y: A numpy array of shape (N,) containing training labels; y[i] = c means
      that X[i] has label c, where 0 <= c < C.
    - reg: (float) regularization strength

    Returns a tuple of:
    - loss as single float
    - gradient with respect to weights W; an array of same shape as W
    """
    # Initialize the loss and gradient to zero.
    loss = 0.0
    dW = np.zeros_like(W)
    
    #############################################################################
    # TODO: Compute the softmax loss and its gradient using explicit loops.     #
    # Store the loss in loss and the gradient in dW. If you are not careful     #
    # here, it is easy to run into numeric instability. Don't forget the        #
    # regularization!                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    num_classes = W.shape[1]
    num_train = X.shape[0]
    
    for i in range(num_train):
        scores = X[i].dot(W)
        scores -= np.max(scores)  # 这里是-最大值，防止出现指数爆炸
        correct_class = y[i]
        exp_scores = np.exp(scores)  # 得分求指数
        loss += -np.log(exp_scores[correct_class]/np.sum(exp_scores)) 
        for j in range(num_classes):
            if j == correct_class:
                # 一定注意下面是+=，因为这是循环遍历每张图片的方式，最后得到的是所有图片的梯度求平均，所以这里没遍历一张图片就把求出来的梯度加起来。
                dW[:, j] += (exp_scores[j]/np.sum(exp_scores)-1) * X[i]
            else:
                dW[:, j] += (exp_scores[j]/np.sum(exp_scores)) * X[i]    
    loss /= num_train
    loss += reg*np.sum(W*W)
    dW /= num_train
    dW += 2*reg*W


    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    return loss, dW

1.2.2.向量化模式

def softmax_loss_vectorized(W, X, y, reg):
    """
    Softmax loss function, vectorized version.

    Inputs and outputs are the same as softmax_loss_naive.
    """
    # Initialize the loss and gradient to zero.
    loss = 0.0
    dW = np.zeros_like(W)

    #############################################################################
    # TODO: Compute the softmax loss and its gradient using no explicit loops.  #
    # Store the loss in loss and the gradient in dW. If you are not careful     #
    # here, it is easy to run into numeric instability. Don't forget the        #
    # regularization!                                                           #
    #############################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    num_classes = W.shape[1]
    num_train = X.shape[0]
    
    scores = X.dot(W)
    correct_class_scores = scores[np.arange(num_train),y]  # 这种访问方式得到的数据就是一个向量
    # print(correct_class_scores.shape) 这里得到的就是一个一维向量
    exp_scores = np.exp(scores)
    exp_scores_sum = np.sum(exp_scores,axis=1)  # 这里得到的也是一个一维向量

    loss += np.sum(np.log(exp_scores_sum)-correct_class_scores)  # 这里用的是loss公式的变形体，方便求
    loss /= num_train
    loss += reg*np.sum(W*W)
    
    margin = exp_scores / exp_scores_sum.reshape(num_train,1)  # reshape是为了能够广播
    margin[np.arange(num_train),y] += -1   # 更改正确类别所在的位，让值-1
    dW = X.T.dot(margin)  # 注意一定是x.T

    dW /= num_train
    dW += 2*reg*W
    

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    return loss, dW

2.Inline questions

Inline Question 1

# First implement the naive softmax loss function with nested loops.
# Open the file cs231n/classifiers/softmax.py and implement the
# softmax_loss_naive function.

from cs231n.classifiers.softmax import softmax_loss_naive
import time

# Generate a random softmax weight matrix and use it to compute the loss.
W = np.random.randn(3073, 10) * 0.0001
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0)

# As a rough sanity check, our loss should be something close to -log(0.1).
print('loss: %f' % loss)
print('sanity check: %f' % (-np.log(0.1)))

Why do we expect our loss to be close to -log(0.1)? Explain briefly.

Y𝑜𝑢𝑟𝐴𝑛𝑠𝑤𝑒𝑟:YourAnswer: 因为选择的权重是符合正态分布的，最后log里面是exp(fyi)/sum(exp(fj))，由于是正态分布此时计算出来的各个类别的得分都是近似的，所以log里面的概率就接近0.1

Inline Question 2

提问：Suppose the overall training loss is defined as the sum of the per-datapoint loss over all training examples. It is possible to add a new datapoint to a training set that would leave the SVM loss unchanged, but this is not the case with the Softmax classifier loss.（判断）

翻译：假设总训练损失定义为所有训练示例中每个数据点损失的总和。 可以将新的数据点添加到训练集，这将使SVM损失保持不变，但是对于Softmax分类器损失而言，情况并非如此。

回答：有可能加的数据点对svm来讲比较好辨识，所以取max之后都是0，但是对于softmax而言，总会得到一个概率分布，然后算出交叉熵，换言之，softmax的loss总会加上一个量，即使是一个很小的量。