? ??图像处理中,"空间域" 指的是图像平面,因此,空间滤波?可定义为:在图像平面内对像素灰度值进行的滤波?
1? 空间滤波?
1.1? 滤波过程
? ? 如图,Filter 是一个 3x3 滤波核,当它从图像的左上角开始,逐个像素沿水平方向扫描,最后到右下角时,便会产生滤波后的图像? ? ??
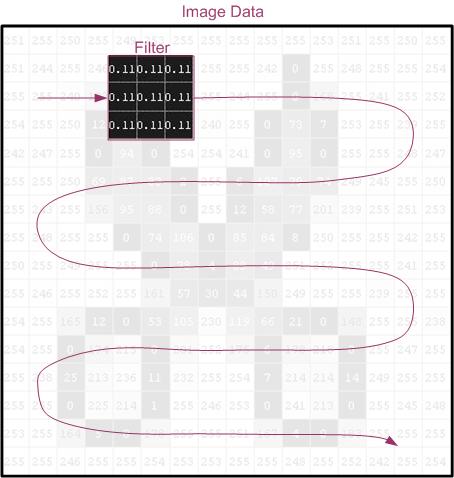
? ?假设输入图像 ,滤波后的图像为?
,则其中?
和?
的计算过程如下:? ? ?

? ? ? ? ? ? ??

? ? 上图中,以像素 (4,4) 为中心的 3x3 邻域,和滤波核的向量点乘之积,即为 g(4,4)?
? ? ? g(4,4) = 240*0.1111 + 183*0.1111 + 0*0.1111 + 250*0.1111 + 12*0.1111 + 87*0.1111 + 255*0.1111 + 1*0.1111 + 94*0.1111
? ? ? ? ? ? ? ? ?= 26.6666 + 20.3333 + 0 + 27.7777 + 1.3333 + 9.6666 + 28.3333 + 0 + 10.4444
? ? ? ? ? ? ? ? ?= 124.55? ? ? ?
1.2? 相关和卷积
? ? 空间滤波中,相关和卷积,是容易混淆的概念,定义如下:
? ? ?-??相关 (Correlation),和上述的滤波过程一样,即 滤波核 逐行扫描图像,并计算?每个位置像素点积?的过程
? ? ?-??卷积 (Convolution),和 "相关" 过程类似,但 滤波核 要?先旋转 180°,然后再执行和 “相关” 一样的操作
? ? ? ? ? ?(二维中的旋转 180°,等于滤波核沿一个坐标轴翻转,然后再沿另一个坐标轴翻转)
? ? ? ? ??
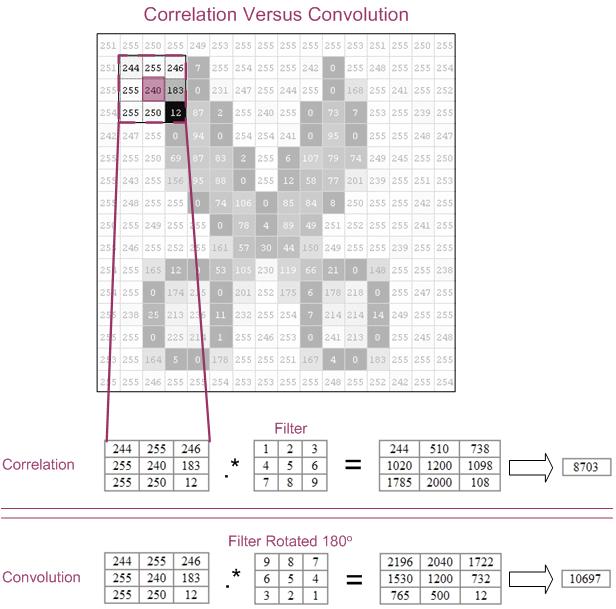
? ??注意:如果滤波核是对称的,则对图像进行相关和卷积的结果是一致的
2? OpenCV 函数
2.1? filter2D()
? ? 在 OpenCV 中,可自定义滤波核,然后通过 filter2D() 来完成图像滤波
void filter2D(
InputArray src, // 输入图像
OutputArray dst, // 输出图像(大小和通道数,同 src)
int ddepth, // 输出图像的 depth
InputArray kernel, // 滤波核,准确地说,是相关核
Point anchor = Point(-1,-1), // 锚点位置,滤波核尺寸为奇数时,不用指定,一般取默认值 Point(-1,-1);滤波核尺寸为偶数时,需指定锚点位置
double delta = 0, // optional value added to the filtered pixels before storing them in dst
int borderType = BORDER_DEFAULT // 边界处理方法
);? ? filter2D() 求的是?相关,并非?卷积,只有当滤波核对称时,filte2D() 才可视为卷积运算,其公式如下:
? ?
? ? 假定滤波核 kernel 大小为 3x3,以一个像素点 src(4,4) 为例,则有:
? ? ? dst(4,4) =? ?kernel(0,0)*src(4+0-1, 4+0-1) + kernel(0,1)*src(4+0-1, 4+1-1) + kernel(0,2)*src(4+0-1, 4+2-1)
? ? ? ? ? ? ? ? ? ? ? + kernel(1,0)*src(4+1-1, 4+0-1) + kernel(1,1)*src(4+1-1, 4+1-1) + kernel(1,2)*src(4+1-1, 4+2-1)
? ? ? ? ? ? ? ? ? ? ? + kernel(2,0)*src(4+2-1, 4+0-1) + kernel(2,1)*src(4+2-1, 4+1-1) + kernel(2,2)*src(4+2-1, 4+2-1)?
? ? 滤波核与输入图像的卷积点乘,对应关系如下:
? ? ??
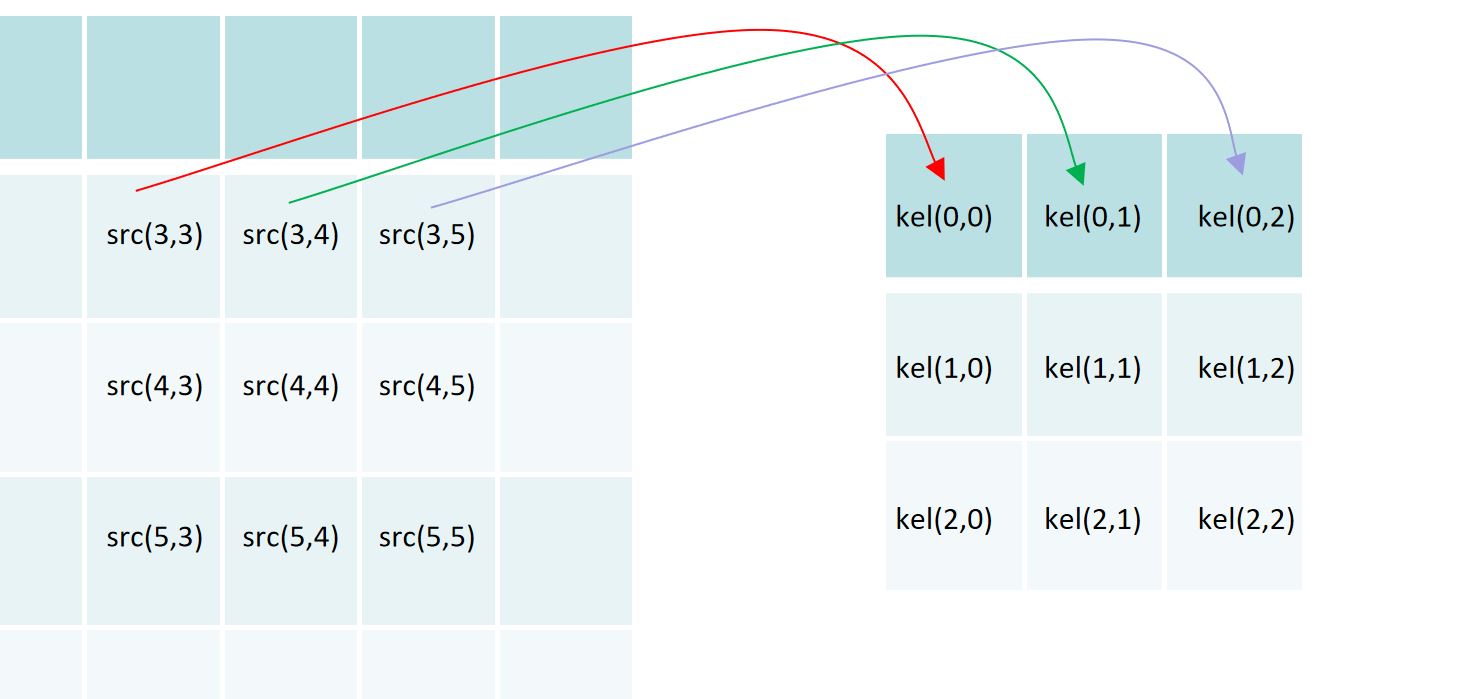
?
2.2? flip()
? ? 当滤波核不对称时,要得到真正的卷积运算,还需 flip() 函数来完成 kernel 的二维翻转
void flip(
InputArray src, // input array
OutputArray dst, // output array
int flipCode // 0, flip around x-axis; positive value, flip around y-axis; negative value, flip around both axes.
);? ? 如果滤波核的大小为奇数,则 filter2D() 中的锚点位置可设为 Point(-1,-1),此时,默认滤波核的中心为锚点;如果滤波核的大小为偶数,则需要自定义锚点位置
? ? OpenCV 中锚点位置的实现函数?normalizeAnchor() 如下:
static inline Point normalizeAnchor(Point anchor, Size ksize)
{
if (anchor.x == -1)
anchor.x = ksize.width / 2;
if (anchor.y == -1)
anchor.y = ksize.height / 2;
CV_Assert(anchor.inside(Rect(0, 0, ksize.width, ksize.height)));
return anchor;
}3? 代码示例
?3.1? 偏导数
? ? 自定义滤波核,利用 filter2D() 函数,实现图像的一阶和二阶偏导运算? ?
???1)? 一阶偏导
? ? 图像在 x 和 y 方向的一阶偏导如下:
? ?
? ?
? ? 对应滤波核为 ,
? ? 2)? 二阶偏导
? ? 同样,在 x 和 y 方向的二阶偏导如下:
? ?
? ?
? ?
? ? 对应滤波核为 ,
,
?3.2 代码示例
#include "opencv2/imgproc.hpp"
#include "opencv2/highgui.hpp"
using namespace cv;
int main()
{
// 读取图像
Mat src = imread("fangtze.jpg", IMREAD_GRAYSCALE);
if (src.empty()) {
return -1;
}
Mat kx = (Mat_<float>(1, 2) << -1, 1); // 1行2列的 dx 滤波核
Mat ky = (Mat_<float>(2, 1) << -1, 1); // 2行1列的 dy 滤波核
Mat kxx = (Mat_<float>(1, 3) << 1, -2, 1); // 1行3列的 dxx 滤波核
Mat kyy = (Mat_<float>(3, 1) << 1, -2, 1); // 3行1列的 dyy 滤波核
Mat kxy = (Mat_<float>(2, 2) << 1, -1, -1, 1); // 2行2列的 dxy 滤波核
// 一阶偏导
Mat dx, dy;
filter2D(src, dx, CV_32FC1, kx);
filter2D(src, dy, CV_32FC1, ky);
// 二阶偏导
Mat dxx, dyy, dxy;
filter2D(src, dxx, CV_32FC1, kxx);
filter2D(src, dyy, CV_32FC1, kyy);
filter2D(src, dxy, CV_32FC1, kxy);
// 显示图像
imshow("dx", dx);
waitKey();
}? ? 输出的偏导图像如下,第一行从左到右:原图 - dx - dy;第二行从左至右:dxy - dxx -dyy
? ? ??

??

??

? ? ??

??

??

参考资料
? OpenCV Tutorials / imgproc module /?Making your own linear filters
? Gonzalez,《Digital Image Processing》4th? ch3 Intesity Transformations and Spatial Filtering
??CS425 Lab: Intensity Transformations and Spatial Filtering