1. 数据获取
1.1 数据挖掘的对象
(1)关系型数据库、事务型数据库、面向对象的数据库;
(2)数据仓库/多维数据库;
(3)空间数据(如地图信息)
(4)工程数据(如建筑、集成电路的信息)
(5) 文本和多媒体数据(如文本、图象、音频、视频数据)
(6)时间相关的数据(如历史数据或股票交换数据)
(7)万维网(如半结构化的HTML,结构化的XML以及其他网络信息)
1.2数据挖掘的步骤
(1)数据清理(消除噪音或不一致数据,补缺);
(2)数据集成((多种数据源可以组合在一起);
(3)数据选择(从数据库中提取相关的数据);
(4)数据变换(变换成适合挖掘的形式);
(5)数据挖掘(使用智能方法提取数据模式);
(6)模式评估(识别提供知识的真正有趣模式);
(7)知识表示(可视化和知识表示技术)。
1.3支持数据挖掘的关键技术
(1)数据库/数据仓库/OLAP
(2) 数学/统计(回归分析:多元回归、自回归;判别分析:Bayes判别、Fisher判别、非参数判别;主成分分析、相关性分析;模糊集;粗糙集)
(3)机器学习(聚类分析;关联规则;决策树;范例推理;贝叶斯网络;神经网络;支持向量机;遗传算法)
(4)可视化:将数据、知识和规则转化为图形表现的形式。
1.4数据仓库
(1)数据仓库是一个面向主题的、集成的、随时间变化的、非易失性数据的集合,用于支持管理人员的决策。
(2)数据仓库是一种多个异种数据源在单个站点以统一的模式组织的存储,以支持管理决策。数据仓库技术苞括数据清理、数据集成和联机分析处理( OLAP) 。
(3)数据仓库的逻辑结构是多维数据库。数据仓库的实际物理结构可以是关系数据存储或多维数据方(Cube) 。
(4)数据方是由维度(Dimension)和度量(Measure)定义的一种数据集,度量存放在由维度索引的数据方单元中。维度对应于模式中的属性组,度量对应于与主题相关的事实数据。数据方的物化是指预计算并存储全部或部分单元中的度量。
1.5数据仓库的模型
(1)**星形模式:**最常见模型;其中数据仓库包括一个大的、包含大批数据、不含冗余的中心表(事实表)﹔一组小的附属表(维表),每维一个。
(2)**雪花模式:**雪花模式是星型模式的变种,其中某些维表是规范化的,因而把数据进一步分解到附加的表中。
(3)**星系模式:**多个事实表共享维表。这种模式可以看作星形模式集,因此称为星系模式,或事实星座。
1.6典型的OLAP操作
(1) OLAP是一种多维数据分析技术。包括汇总、合并和聚集等功能,以及从不同的角度观察信息的能力。
(2上卷: 从某一维度的更高概念层次观察数据方,获得更概要的数据。它通过沿维的概念分层向上或维归约来实现。
(3)下钻: 下钻是上卷的逆操作。它从某一维度的更低概念层次观察数据方,获得更详细的数据。下钻可以通过沿维的概念分向下或引入新的维来实现。
(4)切片和切块: 切片操作在给定的数据方的选择一个维的部分属性,获得一个较小的子数据方。切块操作通过对选择两个或多个维的部分属性,获得一个较小的子数据方
(5)转轴: 是一种改变数据方二维展现形式的操作。它将数据方的二维展现中的某些维度由行改为列,或由列改为行。
2 数据准备
- 现实世界的数据是不完整的(有些感兴趣的属性缺少属性值,或仅包含聚集数据),含噪音的(包含错误,或存在偏离期望的异常值),不一致的(例如,用于商品分类的部门编码存在差异)。
- 需要数据清理、数据集成、数据选择、数据变换等技术对数据进行处理。
2.1 维归约/特征提取
2.1.1决策树归约
(1)决策树归约构造一个类似于流程图的结构:其每个非叶子结点表示一个属性上的测试,每个分枝对应子测试的一个输出;每个叶子结点表示一个决策类。
(2)在每个结点,算法选择“当前对分类最有帮助”的属性,出现在树中的属性形成归约后的属性子集。
2.1.2粗糙集归约
(1)粗糙集理论在数学意义上描述了知识的不确定性,它的特点是把用于分类的知识嵌入集合内,使分类与知识联系在一起。
(2)知识的粒度、不可分辨关系、上近似、下近似、边界等概念见下图。
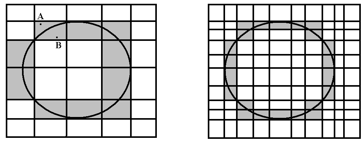
(3)令Q代表属性的集合。
q
∈
Q
q\in Q
q∈Q是一个属性,如果IND(Q-q)= IND(Q),则q在S中不是独立的;否则称q在s中是独立的。
(4)若集合满足IND?= IND(Q)且R中的每一个属性都是独立的,则R被称为Q的一个“约简”,记作R=RED(Q)。
(5)约简可以通过删除冗余的(不独立的)属性而获得,约简包含的属性即为“对分类有帮助”的属性。
2.2 数据变换
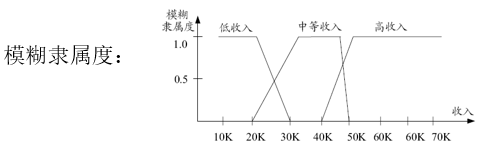
2.2.1归一化与模糊化
有限区间的归一化:
无限区间的归一化:
2.2.2核函数
(1)核函数的基本思想是将在低维特征向量线性不可分的数据映射到线性可分的高维特征空间中去。
(2)映射可以是显式的,也可以是隐式的。显式映射即找到一个映射关系f,使高维空间的特征向量f (x)可以被直接计算出来。
(3)隐式映射,即引入一个核函数进行整体处理,就避免了对的直接求f(x)的计算困难。核函数即某高维特征空间中向量的内积,是核矩阵中的一个元素。
(4)并不是所有的实值函数f(x)都可以作为空间映射的核函数,只有f(x)是某一特征空间的内积时,即符合Mercer条件,它才能成为核函数。
- 多项式函数
- 高斯(RBF)函数
- 多层感知机函数
- 低维空间向量映射到高维空间向量
2.3 数据压缩
2.3.1 离散化
-
离散化的用途:
- (1)适应某些仅接受离散值的算法;
- (2)减小数据的尺度。
-
离散化的方法包括几下几种。
-
(1)等距分割;
-
(2)聚类分割;
-
(3)直方图分割;
-
(4)基于嫡的分割;
-
(5) 基于自然属性的分割。
2.3.2 回归
- 回归和对数线性模型可以用来近似给定的数据。
- 在线性回归中,用一条直线来模拟数据的生成规则。
- 多元回归是线性回归的扩展,涉及多个预测变量。
- 在多项式回归中,通过对变量进行变换,可以将非线性模型转换成线性的,然后用最小平方和法求解。
- 利用线性回归可以为连续取值的函数建模。广义线性模型则可以用于对离散取值变量进行回归建模。
- 在广义线性模型中,因变量Y的变化速率是Y均值的一个函数;这一点与线性回归不同。常见的广义线性模型有:对数回归和泊松回归。
- 对数回归模型是利用一些事件发生的概率作为自变量所建立的线性回归模型。
- 泊松回归模型主要是描述数据出现次数的模型,因为它们常常表现为泊松分布。
2.3.3 主成分分析(PCA)
- PCA算法搜索c个最能代表数据的k-维正交向量;这里c≤k。这样,原来的数据投影到一个较小的空间,导致数据压缩。步骤如下:
(1)对输入数据归一化,使得每个属性都落入相同的区间。
(2)PCA计算c个规范正交向量,作为归一化输入数据的基。这些是单位向量,每一个都垂直于另一个:称为主成分。输入数据是主要成分的线性组合。
(3)对主成分按“意义”或强度降序排列,选择部分主成分充当数据的一组新坐标轴。
2.3.4 离散小波变换(DWT)
- 离散小波变换是一种线性信号处理技术。该技术方法可以将一个数据向量转换为另一个数据向量(为小波相关系数);且两个向量具有相向长度
- 可以舍弃转换后的数据向量中的一些小波相关系数。保留所有大于用户指定阈值的小波系数,而将其它小波系数置为0,以帮助提高数据处理的运算效率。
- 这一技术方法可以在保留数据主要特征情况下除去数据中的噪声,因此该方法可以有效地进行数据清洗。
- 给定一组小波相关系数,利用离散小波变换的逆运算还可以近似恢复原来的数据
3 数据预处理
数据挖掘的前提:真实世界中的数据来源复杂、体积巨大,往往难以避免地存在缺失、噪声、不一致等问题。为了提高数据挖掘的质量,产生了数据预处理技术。
数据和特征决定了机器学习的上限,而所选模型和算法只是去逼近这个上限。
通过特征提取,我们能得到未经处理的特征,这时的特征可能有以下问题:
- 不属于同一量纲:即特征的规格不一样,不能够放在一起比较。
- 信息冗余:对于某些定量特征,其包含的有效信息为区间划分,例如学习成绩,假若只关心“及格”或不“及格”,那么需要将定量的考分,转换成“1和“o表示及格和未及格
- 定性特征不能直接使用:某些机器学习算法和模型只能接受定量特征的输入,那么需要将定性特征转换为定量特征。
- 存在缺失值:缺失值需要补充。
- 信息利用率低:不同的机器学习算法和模型对数据中信息的利用是不同的。
- 当数据的维数过高时还会存在所谓的“维数灾难(Curse of dimensionality)”问题,过高的维度不仅增加了计算量,反而可能会降低算法的效果。
常见的数据预处理方法:
●数据清洗
处理数据的某些纪录值缺失,平滑数据中的噪声、发现异常值,改正不一致等。
●数据融合
将不同来源的、异质的数据融合到一起。良好的数据融合可以减少数据中的冗余和不―致性,进而提升后续步骤的精度和速度。
●数据转换
通过平滑聚集,数据概化,规范化等方式将数据转换成适用于数据挖掘的形式。
●数据降维
将高维度数据化为低维度数据,仍保持原数据的大部分信息,使数据挖掘结果与降维前结果相同或几乎相同。
3.1 数据清洗
3.1.1 缺失值处理
-
缺失值在实际数据中是不可避免的问题,对于不同的数据场景应该采取不同的策略,首先应该判断缺失值的分布情况:
- 如果缺失值极少且这个维度信息不重要,一般删除它们对于整体数据情况影响不大;
- 如果缺失值较多或这个维度的信息还很重要的时候,直接删除会对后面的算法跑的结果造成不好的影响。
-
我们常用的方法有以下几种:
-
直接删除——适合缺失值数量较小,并且是随机出现的,删除它们对整体数据影响不大的情况;
-
使用一个全局常量填充——譬如将缺失值用“unknown等填充,但是效果不一定好,因为算法可能会把它识别为一个新的类别,一般很少用;
-
使用均值或中位数代替:
- 优点:不会减少样本信息,处理简单。
- 缺点:当缺失数据不是随机数据时会产生偏差,对于正常分布的数据可以使用均值代替,如果数据是倾斜的,使用中位数可能更好。
-
插补法
- 1)随机插补法——从总体中随机抽取某个样本代替缺失样本
- 2)多重插补法——通过变量之间的关系对缺失数据进行预测,例如利用蒙特卡洛方法生成多个完整的数据集,在对这些数据集进行分析,最后对分析结果进行汇总处理
- 3)热平台插补——指在非缺失数据集中找到一个与缺失值所在样本相似的样本(匹配样本)利用其中的观测值对缺失值进行插补。
- 4)拉格朗日差值法和牛顿插值法
-
5.建模法——可以用回归、使用贝叶斯形式化方法的基于推理的工具或决策树归纳确定。例如,利用数据集中其他数据的属性,可以构造一棵判定树,来预测缺失值的值。
以上方法各有优缺点,具体情况要根据实际数据分分布情况、倾斜程度、缺失值所占比例等等来选择方法。一般而言,建模法是比较常用的方法,它根据已有的值来预测缺失值,准确率更高。
3.1.2 异常值处理
异常值我们通常也称为“离群点”( outlier),即在样本空间中,与其他样本点的一般行为或特征不一致的点。一般可能有如下产生原因:
- 计算的误差或者操作的错误所致,比如:某人的年龄-999岁,这就是明显由误操作所导致的离群点;
- 数据本身的可变性或弹性所致,比如:一个公司中CEO的工资肯定是明显高于其他普通员工的工资,于是CEO变成为了由于数据本身可变性所导致的离群点。
注意:离群点不一定是无用数据:它也许正是用户感兴趣的,比如在欺诈检测领域,那些与正常数据行为不一致的篱群点,在往预示着嵌诈行为,因此成为执法者所关注的。
-
常见异常值检测方法:
-
1.基于统计分布的离群点检测
这类检测方法假设样本空间中所有数据符合某个分布或者数据模型,然后根据模型采用不和谐校验( discordancy test )识别离群点。例如:-
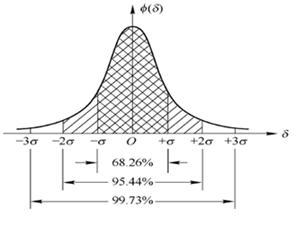
1)3 ? \partial ?原则
如果数据服从正态分布,在3 ? \partial ?原则下,异常值为一组测定值中与平均值的偏差超过3倍标准差的值。如果数据服从正态分布,距离平均值3 ? \partial ?之外的值出现的概率为P(|x-u] > 3 ? \partial ?)<=0.003,属于极个别的小概率事件。如果数据不朋从正态分布,也可以用远离平均值的多少倍标准差来描述。
-
2)箱型图分析
箱型图提供了识别异常值的一个标准:如果一个值小于QL-1.5IQR或大于QU-1.51QR的值,则被称为异常值。QL为下四分位数,表示全部观察值中有四分之一的数据取值比它小;Qu为上四分位数,表示全部观察值中有四分之一的数据取值比它大;IQR为四分位数间距,是上四分位数QU与下四分位数QL的差值,包含了全部观察值的一半。箱型图判断异常值的方法以四分位数和四分位距为基础:四分位数具有鲁棒性∶25%的数据可以变得任意远并且不会干扰四分位数,所以异常值不能对这个标准施加影响。因此箱型图识别异常值比较客观·在识别异常值时有一定的优越性。
-
-
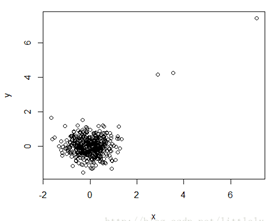
2.基于距离的离群点检测
通常可以在对象之间定义邻近性度量,异常对象是那些远离其他对象的对象。如果样本空间D中至少有N个样本点与对象O的距离大于dmin,那么称对象O是以(至少N个样本点}和dmin为参数的基于距离的离群点。
优点:简单;
缺点:- 基于邻近度量的方法需要o( m 2 m^2 m2)时间,大数据集不适用;
- 该方法对参数的选择也是敏感的,不同的距离度量其结果也不一样;
- 不能处理具有不同密度区域的数据集,因为它使用全局阈值,不能考虑这种密度的变化。
-
3.基于密度的局部离群点检测
当一个点的局部密度显著低于它的大部分近邻时才将其分类为离群点。适合非均匀分布的数据。不同于基于距离的方法,基于密度的离群点检测不将离群点看做一种二元性质,即不简单用Yes or No来断定一个点是否是离群点,而是用一个权值来评估它的离群度。它是局部的,意思是该程度依赖手对象相对于箕领域的孤立情况。这种方法可以向时检测出全局离群点和局部离群点。
优点:给出了对象是离群点的定量度量,并且即使数据具有不同的区域也能够很好的处理;
缺点∶基于距离的方法一样,具有o( m 2 m^2 m2)的时间时间复杂度,对于低维数据使用特定的数据结构可以达到o(mlogm) ;
参数选择困难。仍然需要选择这些离群度的上下界。
异常值处理处理方法:
- 删除异常值——明显看出是异常且数量较少可以直接删除
- 不处理——如果算法对异常值不敏感则可以不处理,但如果算法对异常值敏感,则最好不要用,如基于距离计算的一些算法,包括kmeans,knn之类的。
- 平均值替代——损失信息小,简单高效。
- 视为缺失值——可以按照处理缺失值的方法来处理
3.1.3 数据去重
- 数据去重
数据重复在实际生活中很常见,在一些数据挖掘模型中,这些冗余的数据加大了数据分析的难度和处理速度,因此需要对数据去重。 - 常见方法:
1.遍历数据搜索,复杂度高,仅适用于数据规模较小的情形。
2.哈希表示,生成数据指纹,简单高效,适用于大规模数据,代表算法: - Bitmap:位图法
- SimHash:相似哈希
- 布隆过滤器
3.1.4 数据去噪
-
数据去噪
噪声,是被测量变量的随机误差或方差。我们在上文中提到过异常点(离群点),那么离群点和噪音是不是一回事呢? -
观测量(Measurement)=真实数据(True Data)+噪声(Noise)
-
离群点(Outlier)属于观测量,既有可能是真实数据产生的,也有可能是噪声带来的,但是总的来说是和大部分观测量之间有明显不同的观测值。
-
噪声包括错误值或偏离期望的孤立点值,但也不能说噪声点包含离群点,虽然大部分数据挖掘方法都将离群点视为噪声或异常而丢弃。然而,在一些应用(例如:欺诈检测),会针对离群点做离群点分析或异常挖掘。而且有些点在局部是属手篱群点,但从全局着是正常的。
3.2 数据融合
3.3 数据转换
在对数据进行统计分析时,要求数据必须满足一定的条件,数据转换就是将数据从一种表示形式变为另一种表现形式的过程。常见的数据转换方法大致可分为如下几类:
-
离散化
有些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式。常常需要将连续属性变换成分类属性(离散化,,discretization)。 -
二值化
特征二值化是把数值特征转化成布尔值的过程,其核心在于设定一个阈值,大于阈值的赋值为1,小于等于谢值的赋值为0。这个方法对符合多变量伯努利分布的输入数据进行预测概率参数很有效。
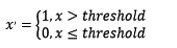
-
归一化
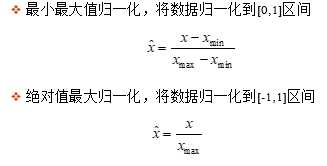
-
标准化
不同的特征有不同的取值范围,如线性模型,特征的取值范围会对最终的结果产生较大的影响,取值范围不一致会导致模型会更偏向取值范围较大的特征。标准化通常是为了消除不同属性或样本间的不齐性,使同一样本内的不同属性间或同一属性在不同样本内的方差减小。另外数据的标准化也会加快数据的收敛速度。例如:
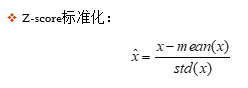
-
正则化
通常是为给数据加入某种限制,使其满足某一特性,常见的:

-
特征编码
如[男性",“来自美国r” ,使用t浏览器”]可以表示成[0,1,3],[“女性”.“来自亚洲”.,"使用chrome浏览器]可以表示成[1,2,1]。这些整数式的表示不能直接作为机器学习模型的参数,因为我们需要的是连续型的输入而具我们通常是有序的翻译这些特征,而不是所有的特征都是有序化的.
将这些类别特征转化成机器学习模型的参数,可以使用的方法是:使用one-of-K或者one-hot编码(独热编码OneHotEncoding)。它可以把每一个有m种类别的特征转化成m种二值特征。
3.4 数据降维
- 维数灾难
指在涉及到向量的计算的问题中,随着维数的增加,计算量呈指数倍增长的一种现象。维度灾难最直接的后果就是过拟合现象,而发生该现象最根本的原因是:- 维度增加时,有限的样本空间会越来越稀疏。因此模型出现在训练集上表现良好,但对新数据缺芝泛化能力的现象。
- 维度增加时,每个样本数据越来越不可能符合所有维度(特征),这使得大部分样本都变成了噪声。
- 数据降维,又称特征降维,是将高维空间的数据集映射到低维度空间,同时尽可能少的丢失数据,或者降维后的数据点尽可能的被区分。
3.4.1 特征选择
寻找最优子集,剔除不相关( irrelevant)或冗余(redundant)的特征,从而达到减少特征的个数,提高模型的紧缺度,减少运行时间,特征选择后留下的特征在选择前后没有变化。常见的特征选择的方法有:
1)过滤方式:将所有特征进行打分,选择最有效的特征。比如,卡方检验、信息增益、相关系数(皮示逊、cos、互信息等〉等。
2)包装方式:将特征组合的选择看做是一个在特征空间的搜索问题,比如启发式的搜索方法等。
3)嵌入方式:将特征选择的过程嵌入到模型训练的过程中,其实也是就是正则化的方法,比如lasso回归、ridge回归等。
3.4.2 特征抽取
特征抽取是指改变原有的特征空间,并将其映射到一个新的特征空间。例如某个特征是一张图片,将这张图片中的点,线条或颜色提取出来并参数化,就是一个特征抽取的过程。常见的特征抽取方法有:
- PCA主成分分析。其思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主元,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。通过协方差矩阵的特征值分解能够得到数据的主成分,PCA的目标是发现特征之间的线性关系,并去除。数据需要去中心化。
- LDA线性判别式分析。使用类别信息,选择使类内方差小而类间方差大的方向作为投影方向,将数据投影到维度更低的空间中,使得投影后的点区分度更高。
- SVD奇异值分解。直接对特征矩阵进行SVD分解,然后近似表示原矩阵。注意,SVD可以获取多个方向上的主成分,而PCA只能获得单个方向上的主成分。
4 聚类方法
4.1 K-means

4.2 决策树(ID3)
- 决定分类属性﹔
- 对目前的数据表,建立一个节点N
- 如果数据库中的数据都属于同一个类,N就是树叶,在树叶上标出所属的类
- 如果数据表中没有其他属性可以考虑,则N也是树叶,按照少数服从多数的原则在树叶上标出所属类别
- 否则,根据平均信息期望值E或GAIN值选出一个最佳属性作为节点N的测试属性
- 节点属性选定后,对于该属性中的每个值:
从N生成一个分支,并将数据表中与该分支有关的数据收集形成分支节点的数据表,在表中删除节点属性那一栏
如果分支数据表非空,则运用以上算法从该节点建立子树。
4.3 关联规则
定义1:关联是两个或多个变量取值之间存在的一类重要的可被发现的某种规律性。
关联可分为简单关联、时序关联、因果关联。
关联分析目的是寻找给定数据记录集中数据项之间隐藏的关联关系,描述数据之间的密切度。
关联分析的结果常有两种:关联规则和序列模式。
关联规则用于寻找在同一个事件中出现的不同项的相关性;
序列模式与此类似,但它寻找的是事件之间时间上的相关性。
定义2:关联规则是描述在一个交易中物品之间同时出现的规律的知识模式,更确切的说,关联规则是通过量化的数字描述物品X的出现对物品Y的出现有多大的影响。
置信度:
关联规则A->B中,A与B同时出现的次数,除以A出现的次数。

置信度体现的是关联规则的可靠程度,如用关联规则([A->B)的置信度较高,则说明当A发生时,B有很大概率也会发生,这样就可能会带来研究价值。
支持度:
某项集在数据集中出现的频率。即项集在记录中出现的次数,除以数据集中所有记录的数量.
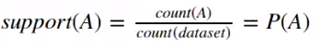
提升度:
关联观见A->B中,提升度是指A->B的置信度,除以B的支持度。

提升度体现的是组合(应用关联规则)相对不组合(不应用关联规则)的比值,如果提升度大于1,则说明应用该关联规则是有价值的。如果提升度小于1,说明应用该关联规则起到了负面影响。因此,我们应该尽可能让关联规则的提升度大于1,提升度越大,则应用该关联规则的效果越好。
同时满足最小置信度阈值和最小支持度阈值的关联规则为强关联规则,是有意义有价值。

关联分析过程关联分析可以分为如下两个过程:
1.从数据集中寻援须繁项集。
2.从频繁项集中生成关联规则。
寻找频繁项集
首先,我们需要能够找到所有的频繁项集,即经常出现在一起的对象集合。实际上,找到频繁项集并不复杂,我们只需要按照如下的步骤来进行操作即可:
1.遍历对象之间所有可能的组合(包括单个对象的组台),每种组合构成一个项集。
2.针对每一个项集A,计算A的支持度[A出现的次数除以记录总数]
3.返回所有支特度大于指定阈值的项集,
Apriori算法原理:
1.如果一个项集是频繁项集,则其所有子集(非空)也是频繁项集。
2.如果一个项集(非空)是非频繁项集,则其所有父集也是非频繁项集。
Apriori算法会从k=1开始,使用两个k项集进行组合,从而产生k+ 1项集。结合之前介绍的算法原理,我们可知,频繁k+ 1项集是由两个k项集组合而成,而对于频繁x+1项集来说,其所有的K项集子集必然是频繁项集,这就意味着,频繁K +1项集只可能从两个预繁xk项集组合产生,因此,当我们在组合的过程中,一旦发现其个K项集不是频繁项集(支持度小于指定的阈值),就可以将其移除,而无需再参与后续生成X+1项集的组合。这样一来,就可以大大减少计算量,
例如在图中,假设(2,3)是非须繁项集,则根据Apriori算法原理,其所有父集也是非频繁项集,故(0.2.3),(1.2.3)与(1.2.3)也是非须繁项集。因此,我们就无需使用(2,3)与其他2项集进行组合,去生成3项集了(因为生成的所有3项集都是非频繁项集),

Apriori算法流程:

生成关联规则
当产生频繁项集后,生成关联规则会相对简单。我们只需要将每个频繁项集拆分成两个非空子集,然后使用这两个子集,就可以构成关联规则。当然,一个频繁项集拆分两个非空子集可能有很多种方式,我们要考虑每一种不同的可能。例,频繁项集({1,2.3)可以拆分为:

然后,我们针对每一个关联规则,分别计算其置信度,仅保留符合最小置信度的关联规则。
4.4 决策树
直观理解
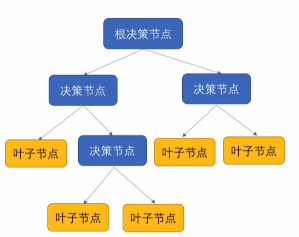
4.4.1 分类树
- 信息熵
信息熵是用来衡量信息不确定性的指标,不确定性是一个事件出现不同结果的可能性。计算方法如下所示:

其中:P(X=i)为随机变量x取值为i的概率
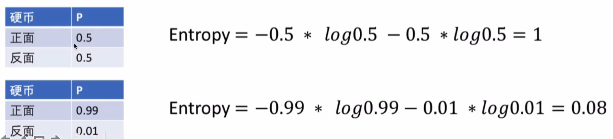
条件熵:在给定随机变量Y的条件下,随机变量X的不确定性
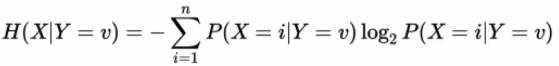
信息增益:熵-条件熵,代表了在一个条件下,信息不确定性减少的程度
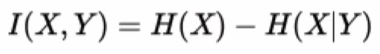

ID3 - 基尼指数(Gini)
基尼指数(Gini不纯度)表示在样本集合中一个随机选中的样本被分错的概率。
注意:Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。当集合中所有样本为一个类时,基尼指数为0.
基尼指数的计算方法:
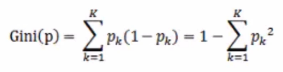
其中,pk表示选中的样本属于第k个类别的概率

CART树是二叉树,对于一个具有多个取值(超过2个)的特征,需要计算以每一个取值作为划分点,对样本D划分之后子集的纯度Gini(D,Ai),然后从所有的可能划分的Gini(D,Ai)中找出Gini指数最小的划分,这个划分的划分点,便是使用特征A对样本集合D进行划分的最佳划分点。
4.4.2 回归树
回归树就是解决回归问题的决策树。
回归树(regression tree),就是用树模型做回归问题,每一片叶子都输出一个预测值。预测值一般是叶子节点所含训练集元素输出的均值。注意:除了使用均值作为预测值,也可以使用其他方法,例如线性回归
回归树的分支标准:标准方差(Standard Deviation)。回归树使用某一特征将原集合分为多个子集,用标准方差衡量子集中的元素是否相近,越小表示越相近。首先计算根节点的标准方差:

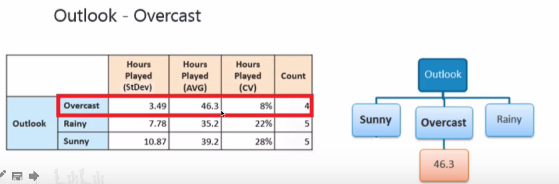
使用标准方差来确定分支,以计算Outlook分支后的标准差为例:



接下来,重复这个过程,使用标准方差降低最多的特征进行分支直到满足某个停止条件,如:
1.当某个分支的变化系数小于某个值(10%)
2.当前节点包含的元素个数小于某个值(3)
使用“outlook”分支以后,值为“Overcast”的分支的变化系数(coefficientof variation)太小(8%),小于我们设置的最小值(10%),停止继续在“Overcast"对应的分支上继续分支,生成一个叶子节点




4.5 集成学习
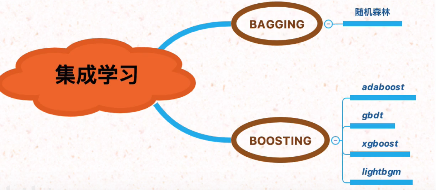
集成学习是通过构建并组合多个学习器来完成学习任务的算法.集成学习常用的有两类:
Bagging:基学习器之间无强依赖关系,可同时生成的并行化方法
Boosting:基学习器之间存在强烈的依赖关系,必须串行生成基分类器的方法随机森林
4.5.1 bagging:随机森林
Bagging


随机森林=bagging+决策树
随机森林:同时训练多个决策树,预测时综合考虑多个结果进行预测,例如取多个节点的均值(回归),或者是众数(分类)。
优势:
1.消除了决策树容易过拟合的缺点
2减小了预测的方差,预测值不会因训练数据的小变化而剧烈变化
随机性体现在两点:
1.从原来的训练数据集随机(带放回bootstrap)取一个子集作为森林中某一个决策树的训练数据集
2.每一次选择分叉的特征时,限定为在随机选择的特征的子集中寻找一个特征
应用:
现有某公司的员工离职数据,我们通过构建决策树和随机森林来预测某一员工是否会离职。并找出影响员工离职的重要特征。
4.5.2 boosting:adaboost
boosting
Boosting方法是将“弱学习算法”提升为“强学习算法”的过程,通过反复学习得到一系列弱分类器(决策树和逻辑回归),组合这些弱分类器得到一个强分类器。Boosting算法要涉及到两个部分,加法模型和前向分步算法。
加法模型就是说强分类器由一系列弱分类器线性相加而成。一般组合形式如下:
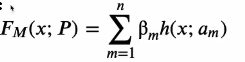
其中,h(x,am)是弱分类器,am是弱分类器学习到的最优参数,βm是弱学习在强分类器中所占比重,P是所有am和βm的组合。这些弱分类器线性相加组成强分类器。
前向分步是在训练过程中,下一轮迭代产生的分类器是在上一轮的基础上训练得来的。即:
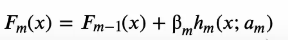
adaboost:
加权
Adaboost的思想是将关注点放在被错误分类的样本上,减小上一轮被正确分类的样本权值,提高被错误分类的样本权值:
Adaboost采用加权投票的方法,分类误差小的弱分类器的权重大,而分类误差大的弱分类器的权重小:
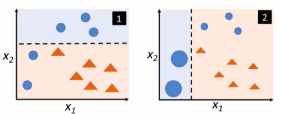
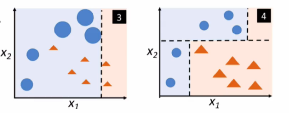
流程:


yi是真实值,Gm是弱分类器,分类错误就要放大,分类正确就缩小

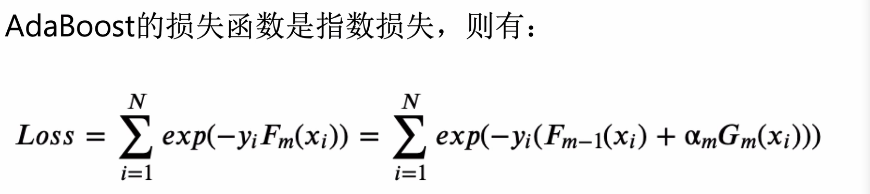
Adaboost可以看作是加法模型、损失函数为指数损失函数、学习算法为前向分布算法时的二分类学习方法。接下来我们使用sklearn中AdaBoost的接口进行实践:

base_estimator 基学习器是什么,n_estimators是弱分类器的个数。
4.5.3 GBDT
梯度
4.5.3.1 BDT
我们先看下简单的提升树(Boosting Decision Tree),提升树是以CART决策树为基学习器的集成学习方法。

第二个弱分类器由训练样本与第一个弱分类器的残差(可理解为没有被第一个弱分类器分出来的数据)来训练


用残差训练T,T在拟合残差,T和残差越接近,loss越小。

4.5.3.2 GBDT
GBDT全称为:Gradient Boosting Decision Tree,即梯度提升决策树,理解为梯度提升+决策树。Friedman提出了利用最速下降的近似方法,利用损失函数的负梯度拟合基学习器:
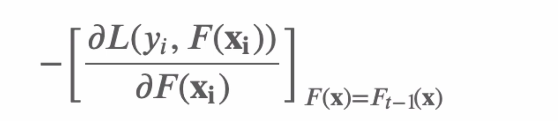
怎么理解这个近似,我们通过平方损失函数来给大家进行介绍。

梯度提升过程:

优化loss很难,所以用负梯度拟合残差,训练加速,

GBDT与提升树的区别是残差使用梯度替代,而且每个基学习器有对应的参数权重。

GBDT的流程(回归)

GBDT的流程(分类)


4.5.4 XGBoost
XGBoost是GBDT的一种,也是加法模型和前向优化算法。
在监督学习中,可以分为:模型,参数,目标函数和学习方法
- 模型:给定输入x后预测输出y的方法,比如说回归,分类,排序等。
- 参数:模型中的参数,比如线性回归中的权重和偏置
- 目标函数:即损失函数,包含正则化项
- 学习方法:给定目标函数后求解模型和参数的方法,比如:梯度下降法,数学推导等。
这四方面的内容也指导着XGBoost系统的设计。
模型形式



目标函数




正则项






学习策略-确定树结构

精确贪心算法:


4.5.5 lightGBM
参考链接:
集成学习:XGBoost, lightGBM