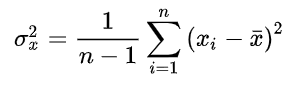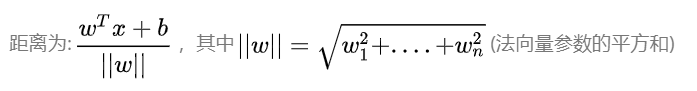[人工智能] 机器学习基础总结

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 机器学习基础总结 -> 正文阅读

[人工智能]机器学习基础总结

分类模型指标

ROC, AUC

accuracy, precision, recall, f-score

我们希望在阈值相同的情况下，假警报率尽可能小，命中率尽可能高，即ROC曲线尽可能陡峭，其对应的AUC值（ROC曲线下方的面积）尽可能高。

模型搭建完成后，有时还需要知道各个特征变量的重要程度，即哪些特征变量在模型中发挥的作用更大，这个重要程度称为特征重要性。

数据预处理

在实际工作中获取到的数据往往不那么理想，可能会存在非数值类型的文本数据、重复值、缺失值、异常值及数据分布不均衡等问题。

非数值型

常用的非数值类型数据处理方法——Get_dummies哑变量处理和Label Encoding编号处理

哑变量
使用pd.get_dummies()来构建哑变量处理非数值型数据。
构造哑变量容易产生高维数据，因此，哑变量常和PCA（主成分分析）一起使用，即构造哑变量产生高维数据后采用PCA进行降维。

Label Encoding编号处理
使用LabelEncoder()函数将文本类型的数据转换成数字。但Label Encoding的一个缺点——可能会产生一些没有意义的关系。树模型（如决策树、随机森林及XGBoost等集成算法）能很好地处理这种转化，因此对于树模型来说，这种奇怪的现象是不会影响结果的。

总结来说，Get_dummies的优点是它的值只有0和1，缺点是当类别的数量很多时，特征维度会很高，此时可以配合使用下一章要讲解的PCA（主成分分析）来减少维度。

如果类别数量不多，可以优先考虑使用Get_dummies，
其次考虑使用Label Encoding或replace()函数；
但如果是基于树模型的机器学习模型，用Label Encoding也没有太大关系。

重复值、缺失值、异常值处理

重复值
data = data.drop_duplicates('c1')

缺失值
isnull(),isna()来查看空值。
空值处理：删除、填补
删除：data.dropna(thresh=2)
填补：data.fillna()

填补均值、用空值上方或下方的值替换空值的方式、还有根据分布情况可以用中位数填充。
如data.fillna(data.mean())，data.fillna(method='pad'),此处的method='pad’表示用空值上方的值来替换空值，如果上方的值不存在或也为空值，则不替换。method='backfill’或method=‘bfill’，表示用空值下方的值来替换空值，如果下方的值不存在或也为空值，则不替换

异常值
两种检测方法——利用箱体图观察和利用标准差检测

箱体图观察

将上四分位数和下四分位数的差值记为IQR，即IQR＝Q3-Q1；令箱体图上界为Q3＋1.5×IQR，下界为Q1-1.5×IQR。
data.boxplot()绘制箱体图

利用标准差

因为3个标准差过于严格，此处将阈值设定为2个标准差，即认为当数值与均值的距离超出2个标准差，则可以认为它是异常值
如果Z-score标准化后的数值大于标准正态分布的标准差1的2倍，那么该数值为异常值，返回布尔值True，否则返回布尔值False。

异常值处理方式

删除
将异常值视为缺失值，利用上文方法处理
数据分箱方法（见后）

多重共线性问题

多重共线性多个变量的情况如：根据3个朝向的数字就能判断第4个朝向的数字是0还是1）

样本不平衡

过拟合

正则化

正则化为了解决过拟合为问题，分为L1和L2正则化。

L1 正则化。向量中各元素绝对值之和，逼近于0。又叫做稀疏规则算子（Lasso regularization）。关键在于能够实现特征的自动选择，参数稀疏可以避免非必要的特征引入的噪声；

L2 正则化。使得每个元素都尽可能的小，但是都不为零。在回归里面，有人把他的回归叫做岭回归（Ridge Regression），也有人叫他 “权值衰减”（weight decay）。

L1 会趋向于产生少量的特征，而其他的特征都是 0，而 L2 会选择更多的特征，这些特征都会接近于 0.

PCA主成分分析

介绍

找出数据里最主要的方面，用数据里最重要的方面代替原始数据。因此**主成分分析**是一种线性变换，把数据变换到一个新的坐标系统中，使得任何数据投影的第一大方差在第一个坐标（称为第一主成分）上，第二大方差在第二个坐标上，以此类推。

PCA的目的是为了让映射后的样本具有最大的发散性。

保留低阶主成分，忽略高阶主成分。低阶主成分通常能保留住数据的最重要的方面。

算法步骤

把矩阵X从n x m维降到n x k维的矩阵Y，找到这样的矩阵W维度为m x k，

将原始数据按列组成n行m列矩阵X
将X的每一行(代表一个属性字段)进行零均值化，即减去这一行的均值（中心化）
求出**协方差**矩 $C=\frac{1}{m}XX^T$

根据下面的解释，是找X的n个随机变z：

对角线上的元素是各个随机变量的方差，非对角线上的元素是两两随机变量之间的协方差，该矩阵为对称矩阵。
求出该协方差矩阵的特征值、特征向量

通俗地说，任意一个协方差矩阵都可以视为线性变换的结果。

对于任何对称矩阵，存在一个特征值分解 $\sum = U\bigwedge U^T$ ，U的每一列都是相互正交的特征向量，且是单位向量，满足 $U^T U=I$ ，对角矩阵对角线上的元素从大到小是特征值，非对角线上的元素都是0！
将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵W，W维度为m x k，实现矩阵Y=XW

中心化是为了后续参与统计运算，比如求方差就包括了x-u

协方差：协方差则一般用来刻画两个随机变量的相似程度。

方差：用来度量单个随机变量的离散程度。因此方差可以视作随机变量x关于其自身的协方差Conv(x,x)

应用

特征工程数据降维，同时保持数据集的对方差贡献最大的特征。

非监督学习的降维方法，只需要特征值分解，就可以对数据进行压缩、去噪。

降维的必要性：

多重共线性可能使解空间不稳定，影响结果的稳定性。
高维空间具有稀疏性

优缺点

优点

仅需要以方差衡量信息量，不受数据集以外的因素影响
各主成分之间正交，可消除原始数据成分间的相互影响的因素。
计算方法简单，主要运算是特征值分解，易于实现。

缺点

主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。
方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。
如果数据很多，协方差计算维度很大

决策树

决策树是一种基本的分类与回归方法，其模型就是用一棵树来表示整个决策的过程，这棵树可以是二叉树也可以是多叉树。根节点包括整个样本集，每一个叶子节点都对应一个决策结果，每一个内部节点对应一个决策过程。因此从根节点到每个叶子节点的路径对应一个判定序列。

回归决策树划分标准不是基尼系数or信息熵，而是均方误差MSE。value是均值。

决策树通过学习简单的决策规则IF-THEN从而预测目标变量的值，从上而下，每一次迭代就是选择一个特征属性进行交叉，直到不能分叉位置。

决策树的生成过程

选择特征：ID3优先选择信息增益最大的，
- ID3使用信息增益作为选择特征的准则
  
  熵用于表示随机变量不确定性的度量
  
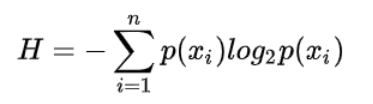
  信息增益 = 信息熵 - 条件熵
  选择信息增益最大的特征，直到剩余特征的信息增益小于阈值、或已经没有特征可以选择时终止。
- C4.5 使用信息增益比作为选择特征的准则
  
  信息增益比 = 信息增益 / 划分前熵
- CART使用GINI指数作为选择特征的准则
  
  基尼指数反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。基尼指数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（率）正好相反。
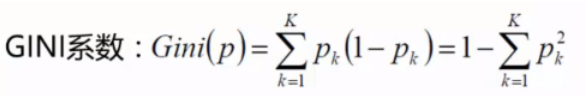
决策树生成：通常是利用信息增益最大、信息增益比最大、Gini 指数最小作为特征选择的准则。从根节点开始，递归的生成决策树。相当于是不断选取局部最优特征，或将训练集分割为基本能够正确分类的子集；
对决策树进行剪枝优化，预防树的过拟合，增强泛化能力。构建决策树的损失函数，将每一个叶子节点回缩到上一层父节点，对损失函数最小的叶节点进行修剪。

剪枝策略

预剪枝（边建立、边剪枝）：在构造过程中，对每个节点在划分前先进行评估，当某个节点满足剪枝条件，则直接停止此分支的构造。可以控制树的深度（最常），叶子节点个数、叶子节点样本数、信息增益量等。

后剪枝：先从训练集生成一颗完整的决策树，然后自底向上对非叶节点进行考察，若将该节点对应的子树替换为叶节点，能带来泛化性能的提升，则将该子树替换为叶节点。C4.5就后剪枝

决策树优缺点

优点：

易于理解和解释，输出树形图解释性较强，容易提取出规则。
对输入数据的属性要求较低。对异常值不敏感

可以同时处理标称型（有限，如真与假）和数值型（无限）的数据；可以处理有缺失属性的样本；能处理不相关的特征；

缺点：

在数据集特征维度很多时，决策树会生成很多枝干，或者树很深，容易发生过拟合，结果不稳定
容易忽略数据集中属性的相关关联
判定过程过于规则，因此在垃圾邮件分类中容易被攻击

改进

剪枝
使用基于决策树的combination算法，如bagging算法，randomforest算法，可以解决过拟合的问题；

应用场景

分类（银行客户贷款分类、垃圾邮件分类）
作为复杂机器学习模型的基础模型（随机森林）

不同的决策树算法辨析

ID3

优点

理论清晰、方法简单、学习能力较强

缺点:

只能用于处理离散分布的特征，不能处理连续的数据，并且对缺失值敏感；
ID3会越分越细，导致过拟合
ID3 没有剪枝策略，容易过拟合
信息增益准则对可取值数目较多的特征有所偏好，类似“id”这种编号的特征其信息增益接近于 1（因为自身熵值极大，它的特征的熵值为0，所以信息增益率会很高）；

C4.5

优点：克服了 ID3 仅仅能够处理离散属性的问题还能处理连续特征、会分割太细的问题、以及信息增益偏向选择取值较多特征的问题，使用后剪枝策略来预防过拟合

连续值的排序运算：先将特征取值排序，以连续两个值中间值作为划分标准。尝试每一种划分，并计算修正后的信息增益，选择信息增益最大的分裂点作为该属性的分裂点。

分割太细分母增加，信息增益率会降低。

缺点：

C4.5 只能用于分类；
C4.5 使用的熵模型拥有大量耗时的对数运算，处理连续值特征还有排序运算；
信息增益率对可取数目较少的属性有所偏好（分母越小，整体越大）

CART

使用基尼指数，因此减少了大量的对数运算，偏向于特征值较多的特征；

生成的树必须是二叉树（C4.5, ID3是多叉树）；

优点

可以回归、也可以分类；（C4.5、ID3只可以分类）
可以连续也可以离散（ID3只可以离散）
二叉树计算速度很快

总体区别

在这里插入图片描述

树的集成算法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-egHx2ZTf-1630397038456)(F:/%E6%96%87%E6%A1%A3/youdao/changreal@163.com/d6938c203ba64101b2b5ad4c0f6fa95c/clipboard.png)]

Bagging和boosting

Bagging（并联）：并行地训练一堆分类器，各分类器之间没有依赖关系。bagging是有放回的选择样本，所有的样本权重保持不变。理论上越多树越好，但实际上超过一定数量结果就差不多上下浮动了。bagging采用并行计算的方式，可以同时生成所有的弱分类器。预测的时候，所有弱分类器的权重相等。

Boosting（串联）：基于提升的迭代算法。每次训练过程中，新增的树是基于预测错分类的样本点，给这些样本点更多的权重，然后权重被更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代进行下去。也就是说新分类器会把注意力放在之前分类效果不好的样本上。各分类器之间有依赖关系，必须串行。boosting采用顺序计算的方式，各个分类器只能按顺序生成，后一个分类器的参数会用到前一个分类器的结果。预测的时候，每个弱分类器都有相应的权重，分类误差越小，权重越高。

比如XGboost, Adaboost, GBDT

Bagging + 决策树 = 随机森林
AdaBoost + 决策树 = 提升树
Gradient Boosting + 决策树 = GBDT

随机森林

介绍

是多重决策树的组合，而不只是一棵决策树。让很多决策树一起工作，可以进行回归、分类。采用大多数决策树的输出结果作为最终预测结果。

针对回归问题，通过随机森林中所有决策树预测值的平均值计算得出最终预测值。（软投票）

针对分类问题，随机森林中的每棵决策树会预测最新数据属于哪个分类。最终，哪一分类被选择最多，就预测这个最新数据属于哪一分类。（硬投票）

随机森林（Random Forest）是 Bagging 的一个变体。Ramdon Forest 在以决策树为基学习器构建 Bagging 集成的基础上，进一步在决策树的训练过程中引入随机属性选择。

随机森林模型会在原始数据集中随机抽样，构成n个不同的样本数据集，然后根据这些数据集搭建n个不同的决策树模型，最后根据这些决策树模型的平均值（针对回归模型）或者投票情况（针对分类模型）来获取最终结果。
数据随机、特征随机（k=根号M）。

Bagging（并联）：并行地训练一堆分类器，各分类器之间没有依赖关系。bagging是有放回的选择样本，所有的样本权重保持不变。理论上越多树越好，但实际上超过一定数量结果就差不多上下浮动了。bagging采用并行计算的方式，可以同时生成所有的弱分类器。预测的时候，所有弱分类器的权重相等。

Boosting（串联）：基于提升的迭代算法。每次训练过程中，新增的树是基于预测错分类的样本点，给这些样本点更多的权重，然后权重被更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代进行下去。也就是说新分类器会把注意力放在之前分类效果不好的样本上。各分类器之间有依赖关系，必须串行。boosting采用顺序计算的方式，各个分类器只能按顺序生成，后一个分类器的参数会用到前一个分类器的结果。预测的时候，每个弱分类器都有相应的权重，分类误差越小，权重越高。

Boosing就是培养精英和重视错误。

“培养精英”就是每一轮训练后对预测结果较准确的弱学习器给予较大的权重，对表现不好的弱学习器则降低其权重。在最终预测时，“优秀模型”的权重是大的，相当于它可以投出多票，而“一般模型”只能投出一票或不能投票。
“重视错误”就是在每一轮训练后改变训练集的权值或概率分布。通过提高在前一轮被弱学习器预测错误的样例的权值，降低前一轮被弱学习器预测正确的样例的权值，来提高弱学习器对预测错误的数据的重视程度，从而提升模型的整体预测效果。

比如XGboost, Adaboost, GBDT

Bagging + 决策树 = 随机森林
AdaBoost + 决策树 = 提升树
Gradient Boosting + 决策树 = GBDT

构建步骤

抽取样本：每棵树的样本是通过有放回的方式从样本总体中随机抽取的

随机采样：随机打乱、拿噪音点等。
抽取特征：每棵树都会随机选择k个特征，然后采用决策树算法（ID3, C4.5, CART)来构建一课决策树

K控制了随机性的引入程度，是一个重要的超参数
构建多课决策树（建立树的过程是同时运行的）
采用多数投票法输出最后的决策结果

应用场景

预测贷款风险，银行or证券使用较多；
预测股票涨跌。

优势劣势

优势

有效解决决策树过拟合问题，能够处理特征维度很多的数据（决策树就适合少的）
对数据的适应能力强，可以处理离散和连续的，无需要规范化
可解释性强，训练完后可以给出哪些feature比较重要，可以可视化分析

我的携程预测方法里就用了feature_importance来查看。

判断方法有两种，树中特征出现的位置来判断；
可以解决回归和分类问题
不同决策树可以由不同主机并行训练生成，效率很高
由于每次不再考虑全部的属性，而是一个属性子集，所以相比于 Bagging 计算开销更小，训练效率更高；

劣势

特征维度较小的数据不适合采用
相对于决策树来说要花费更多时间来训练

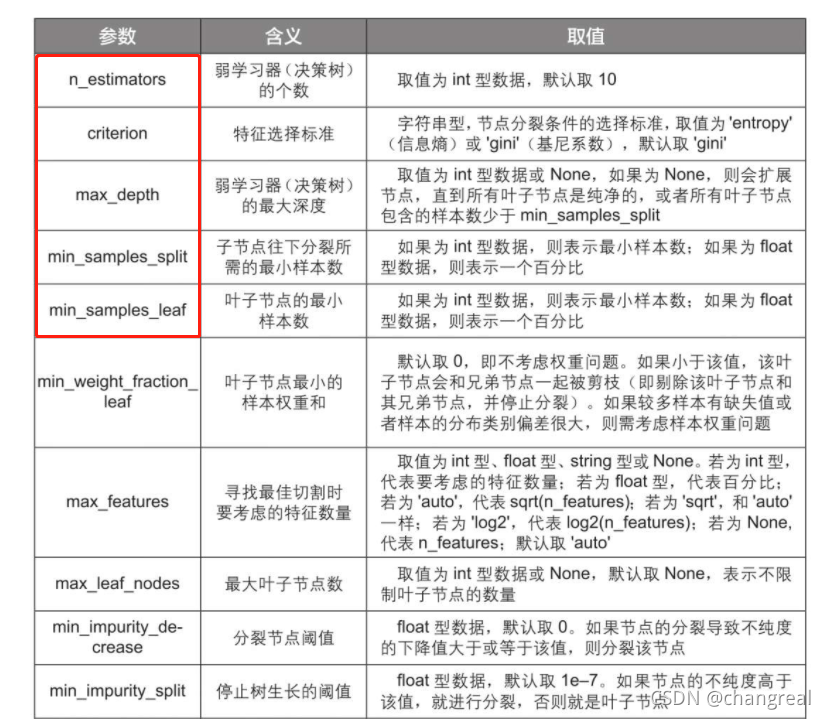
代码常用参数
在这里插入图片描述

逻辑回归

介绍

评估事件发生概率的分类模型，适用于计算二分类问题。

前提假设是样本符合伯努利分布（离散型机率分布）。很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型。

逻辑回归就是线性回归+sigmoid。

离散特征的增加和减少都很容易，易于模型的快速迭代。

离散化后的特征对异常数据有很强的鲁棒性，能增强泛化能力

特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险

在逻辑回归里，应用到sigmoid函数作为预测函数，将ax+b加权和（在线性回归基础上）映射到0-1的范围空间里。在进行分类判断时，设定一个概率的阈值，大于阈值则样本预测值为1，小于阈值则样本预测为0。

线性回归优化目标函数用的最小二乘法

最小二乘法：误差平方和最小

sigmoid函数：在z=0的时候十分敏感，而在z>>0和z<<0的时候都不敏感。

目标函数利用**极大似然估计法（对数似然函数作为损失函数），结合梯度下降法**来估计逻辑回归的参数。

极大似然估计：利用已知样本信息结果，反推最有可能（最大概率）导致这些样本结果出现的模型参数值（模型已定，参数未知）

对数极大似然ylogy+(1-y)log(1-y)

优缺点

优点：

模型输出即为样本的概率分布、构建的模型可解释性高
不需要太多变量，不容易过拟合，泛化能力强，比较稳定，但是有时不够精确

缺点：

预测结果呈S型分布，两端的概率变化非常小，中间的概率变化十分剧烈，难以找到阈值；
拟合能力不好；只能处理线性可分类的问题

应用

二分类领域，得出概率值，适用于根据分类概率排名的领域，比如搜索排名
实际应用：广告点击行为预测、借款人评估、测量市场营销的成功度、预测某个产品的受益、特定的某天是否会发生地震
商业实战中常以基于逻辑回归的评分卡模型为基础（稳定性强，半年到一年更新一次，但不够精确，KS值不够大），再结合决策树等树模型（不太稳定，可能要一个月更新一次，但拟合度强，区分度高，可以在第一拨快速去掉违约人员）。

朴素贝叶斯

介绍

贝叶斯定理可以理解成下面的式子：

后验概率（新信息出现后的A概率）　＝　先验概率（A概率）ｘ可能性函数（新信息带来的调整）

P(A|B)称为"后验概率"

P(A)称为"先验概率"（Prior probability）

P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，也就是新信息B带来的调整，作用是将先验概率（之前的主观判断）调整到更接近真实概率。

朴素贝叶斯通过特征的概率来预测分类，模型是不需要调参的：

训练分类器，计算输入的训练样本中，每个不同的分类类别在训练样本中出现的频率以及每个类别下各个特征属性出现的条件概率值。

先计算先验概率P(类别)、可能性函数P(特征|类别) /P(类别)
根据公式，计算在该样本出现的条件下，各个分类类别出现的概率，哪个概率最大，待分类的样本就属于哪个类别

P(类别|特征) = 先验*可能性函数

条件独立性假设

朴素贝叶斯法对条件概率分布做了条件独立性的假设

假设特征之间相互独立，那么我们统计的时候，就需要在整个特征空间中去找，比如统计p(不帅、性格不好、身高矮、不上进|嫁)。由于数据的稀疏性，很容易统计到0的情况。这样是不合适的。

应用场景

主要用于文本分类（多分类）、垃圾邮件分类等
垃圾邮件过滤、翻译、搜索、中文分词；
情感分类
投资策略；无人驾驶更新地图信息；
肿瘤预测模型。

优缺点

优点

对数据（缺失数据）不敏感，算法简单易懂，常用于文本分类
对小规模数据表现很好，能够处理多分类问题
对大数量训练和查询的时候具有较高的速度，即使超大规模数据及，也会有相对较少的特征数，仅是特征概率的数学运算

缺点

需要计算先验概率
分类决策存在错误率，相比于其他经典的机器学习模型，朴素贝叶斯模型的泛化能力稍弱
使用了样本属性的独立性假设，因此对于样本属性有关联时效果不好（在实际中不太容易成立，因此属性相关度小的时候性能最好）

常见类型的贝叶斯

高斯朴素贝叶斯：特征变量是连续变量，符合高斯分布。比如说人的身高、物体长度等。如果连续变量不是正态分布，需要先转为正态分布。

伯努利贝叶斯：特征变量是离散变量。在文本分类中特征变量体现在一个单词的出现次数、或者单词的**TF-IDF**值。是一种典型的文本分类模型。

TF-IDF

支向量机SVM

介绍

线性可分SVM

二分类模型，求解出正确划分数据集并且找出几何间隔最大的超平面。对于一个线性可分的数据集来说，这种超平面有无数多个，但是几何间隔最大的超平面却是唯一的。

超平面由法向量w和截距b决定。

距离该超平面最近的点（圈出来的点）就是支持向量

支持向量到超平面的距离之和为 $\frac{2}{||w||}$ , SVM的目标就是使得这个距离之和最大化，即||w||最小化。可以借助拉个朗日来计算极值，但是推理过程我不太了解。

线性可分：可以用一个线性函数把两类样本分开，比如二维空间中的直线、三维空间中的平面以及高维空间中的线性函数

线性不可分：指有部分样本用线性分类面划分时会产生分类误差的情况。

为什么要软间隔最大化？

因为如果训练数据线性可分，会存在无数个超平面，利用软间隔最大化的原理可以得到唯一解。近似可分的时候，可以引入松弛变量，求解软间隔最大化，此为线性支持向量机。

线性不可分SVM

需要核函数技巧和软间隔最大化来学习非线性SVM

核函数把原始样本从现有空间映射到一个更高维的空间，使得样本在高位空间线性可分。

常见核函数：

线性核：样本数量小于特征数，选择线性核。K(x,z)=x*z
高斯核：参数相对少，大样本or小样本都有很好的效果。优先使用高斯核or线性核。
样本数量大于特征数目，可以使用非线性核，将样本映射到更高的维度：如高斯核、多项式核
样本数量等于特征数量，也可以高斯核
多项式核：核参数较多。

优缺点

优点

少数支持向量决定了最终结果，对异常值不敏感！
计算复杂度取决于支持向量的数量，而不是样本空间的维度，避免了维度灾难。因此可以解决高维问题
SVM是凸优化问题，求得的解是全局最优解而不是局部最优（相对于神经网络等算法）

缺点

主要用于二分类。多分类问题可以通过多个二分类在支持向量机来解决。
对缺失数据敏感
对非线性问题没有通用解决方案，有时候很难找到一个合适的核函数
对参数和核函数的选择比较敏感。

KNN算法

介绍

KNN是一种有监督的分类算法，给定训练数据集（包括特征和分类结果），输入测试集特征，利用距离函数来判断训练集中与预测集样本最相近的K个实例，这k个实例多属于哪一个类，则就是预测样本的分类。即是知道了结果去验证结果是否正确。

K近邻算法的原理非常简单：对于一个新样本，K近邻算法的目的就是在已有数据中寻找与它最相似的K个数据，或者说“离它最近”的K个数据，如果这K个数据大多数属于某个类别，则该样本也属于这个类别。KNN需要标准化。
数据标准化的常见方法有min-max标准化（也称离差标准化）和Z-score标准化（也称均值归一化）

步骤如下：