[人工智能]DQN学习笔记

本文是DQN的学习笔记，学习内容为知乎上关于DQN的介绍。

原文链接为https://zhuanlan.zhihu.com/p/21262246?refer=intelligentunit

机器学习与RL：

增强学习在某种程度上也可看成机器学习的一种：

做很多次实验，每次实验得到一组数据样本 { ( s 0 , a 0 , r 0 ) , ( s 1 , a 1 , r 1 ) , . . . , ( s t , a t , r t ) } \{(s_0,a_0,r_0),(s_1,a_1,r_1),...,(s_t,a_t,r_t)\} {(s0?,a0?,r0?),(s1?,a1?,r1?),...,(st?,at?,rt?)}，很多次这样的实验构成我们的数据样本集。根据数据样本集进行学习，找到最好的policy。

其中 τ : = { ( s 0 , a 0 ) , ( s 1 , a 1 ) , . . . , ( s t , a t ) } \tau:=\{(s_0,a_0),(s_1,a_1),...,(s_t,a_t)\} τ:={(s0?,a0?),(s1?,a1?),...,(st?,at?)}称为某次实验的轨迹。

可以认为目标函数就是total reward，然后我们的目标就是最大化total reward。

上面的每组实验可以看做是机器学习中的某次优化目标函数的实验。机器学习中有GD，增强学习中应该也有相应的算法。

Value func and action value func：

增强学习(RL)的目标是找一个policy最大化return：
$$G_t=\sum _{k=0}^{\infty }{\lambda }^k{R}_{t+k+1}$$
但除非整个过程结束，否则显然我们无法获取所有的reward来计算出每个状态的Return。

因此，引入一个概念: 价值函数Value Function,用value function $v(s)$来表示一个状态未来的潜在价值
$$v(s)=E[G_t|S_t=s]$$
实际处理时往往是最大化value function。这里的E代表对t时刻之后所有时刻的reward取期望。

注：设$\theta$代表某个policy对应的参数，由于

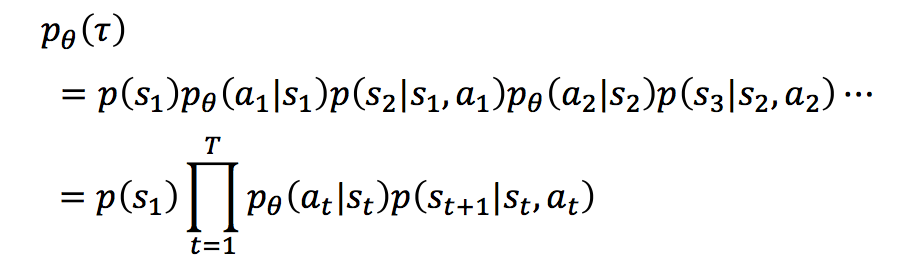
所以上述期望实际需要对以下三种随机性取：

1-不同的策略, 即不同的$\theta$

2-每种策略对应的概率分布，即$p_{\theta }(a_t|s_t)(?t)$

3-给定当前状态和action之后，下一时刻状态的概率分布$p(s_{t+1}|s_t,a_t)(?t)$

前面提到因为$G_t$没法计算所以才引入$v(s)$的，那么$v(s)$怎么计算呢？就需要借助Bellman方程：
$$v(s)=E[R_{t+1}+\lambda v(S_{t+1})|S_t=s]$$
即当前状态的价值只和当前状态的reward以及下一步的价值有关。因此可以用迭代的方法来计算value func！！！

这里的E代表对$S_{t+1}$即下一时刻的状态以及$R_{t+1}$取期望。因此把需要取期望的随机性从所有的t简化为了当前时刻t。

按定义其为：
$$\sum _{s^{\prime },r}p(s^{\prime },r|s)[r+\lambda v(s^{\prime })]$$
value function不依赖于策略，但实际更常用的是依赖于策略的value function，称之为action value function，其定义为
$$Q^{\pi }(s,a):=E[\sum _{k=0}^{\infty }{\lambda }^k{r}_{t+k+1}|s,a]=E[r_{t+1}+\lambda Q^{\pi }(s^{\prime },a^{\prime })|s,a]$$
即该函数既依赖于状态s，又依赖于动作a。这里第二个等号根据的是bellman方程。这里的r仍然代表reward，但表示的是给定某个策略$\pi$之后的reward。

第一个E代表对接下来所有时刻的所有可能的状态取期望，但由于这时策略$\pi$已知，所以实际上这里是对$p_{\theta }(a_t|s_t)(?t),p(s_{t+1}|s_t,a_t)(?t)$取期望。

第二个E把需要取期望的随机性从所有的t简化为了当前时刻t。

我们希望找到能让$Q^{\pi }(s,a)$最大的那个策略，即
$$Q^{?}(s,a)=\underset{\pi }{\max }{Q}^{\pi }(s,a)$$
由于
$$Q^{?}(s,a)=E[r_{t+1}+\lambda Q^{?}(s^{\prime },a^{\prime })|s,a]$$
由于$Q^{?}$是所有策略对应的$Q$值中最大的那个，所以其对应的策略采取的行为$a^{\prime }$自然也是最优的，即a‘是让$Q^{?}$最大的a值。

Value iteration：

那么怎么得到最好的策略$\pi$呢？可以使用所谓的Value iteration（注意这个迭代使用的是value func, 而不是action value func）：

根据定义，
$$\begin{gathered} v^{?}(s)=\underset{a}{\max }E[R_{t+1}+\gamma v^{?}(S_{t+1})|S_t=s,A_t=a] \\ =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v^{?}(s^{\prime })] \end{gathered}$$
对应的迭代形式为：
$$\begin{gathered} v_{k+1}(s)=\underset{a}{\max }E[R_{t+1}+\gamma v_k(S_{t+1})|S_t=s,A_t=a] \\ =\underset{a}{\max }\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma v_k(s^{\prime })] \end{gathered}$$

Q-Learning:

注意Value iteration的每次更新实际是在更新一个函数，因此每次需要对每个状态s都要遍历更新一遍，并且因为要关于a取最大值，所以每次也需要对所有的a遍历一下。

但实际情况下我们没办法遍历所有的状态，还有所有的动作，我们只能得到有限的系列样本。Q-learning针对Value iteration的这个缺陷给出了解决的办法，其对应的更新方法类似于GD/SGD:
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\lambda \underset{a\in A}{\max }Q(S_{t+1},a)?Q(S_t,A_t)]$$
其中$\alpha$是学习率, A = { A 1 , . . . , A t , . . . } A=\{A_1,...,A_t,...\} A={A1?,...,At?,...}

注意这里并不需要用到所有状态s下的Q值。只需要知道对于所有可能的$(S_t,A_t)$对应的Q值即可。因此可以用矩阵来存储所有的Q值。

Q-Learning的缺陷：维数灾难

显然状态s，行动a的所有可能取值决定了储存Q值的矩阵的大小。因此当状态s的可能取值太大时Q储存Q矩阵所用空间就会过大。

一个可能的解决办法是不再记录所有可能的Q值而是用一个函数$f(s,a)$来近似$Q(s,a)$。因此只需要知道$f$的所有参数就可以确定下来Q在任意状态和行动下的$Q$值了。

DQN：

怎么确定下来$f$呢？DQN给出的方案是跟DL结合，使用CNN表示$f$, 因此$f$的确定转化为了训练CNN。而训练CNN需要训练样本。这些样本的自变量当然是不同的状态s（知乎上解释了为什么没有行动a），但是样本的标签怎么确定呢？

回忆Q-learning算法：
$$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\lambda \underset{a\in A}{\max }Q(S_{t+1},a)?Q(S_t,A_t)]$$
我们的最终目标是让$Q(S_t,A_t)=R_{t+1}+\lambda {\max }_{a\in A}Q(S_{t+1},a)$，因此只需取标签为等式右边的值即可。故CNN对应的目标函数为：
$$L(w)=E[r+\lambda \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },w)?Q(s,a,w){]}^2$$
这里w代表CNN的权重，Q代表CNN代表的函数。

我的理解是这里的E代表的是样本平均值。