IRIS数据集介绍:https://baike.baidu.com/item/IRIS/4061453?fr=aladdin
后面代码操作以IRIS鸢尾花数据集为例解析
import numpy as np #科学计算
import pandas as pd #数据清理
import matplotlib.pyplot as plt #可视化
plt.rcParams['axes.unicode_minus'] = False ## 解决坐标轴刻度负号乱码
plt.rcParams['font.sans-serif'] = ['Simhei'] # 设置中文显示,KaiTi,FangSong
from sklearn.datasets import load_iris #鸢尾花IRIS数据集
iris = load_iris()
iris.data.shape
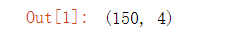
文章目录
一、基本概念
定义:
特征工程是将原始数据转换为更好地代表预测模型的潜在问题的特征的过程,从而提高对未知数据预测的准确性
在数据挖掘中:特征工程=数据准备
常用的特征工程方法包括:
- 数据预处理
- 特征构造
- 特征选择
- 特征转换
- 特征学习
二、数据预处理
2.1 数据清洗(使用Pandas)
看下面这篇文章学习:
https://bigxie.blog.csdn.net/article/details/119007040
 注:非需求数据清洗简单来说就是把不要的字段删了
注:非需求数据清洗简单来说就是把不要的字段删了
补充:箱线图
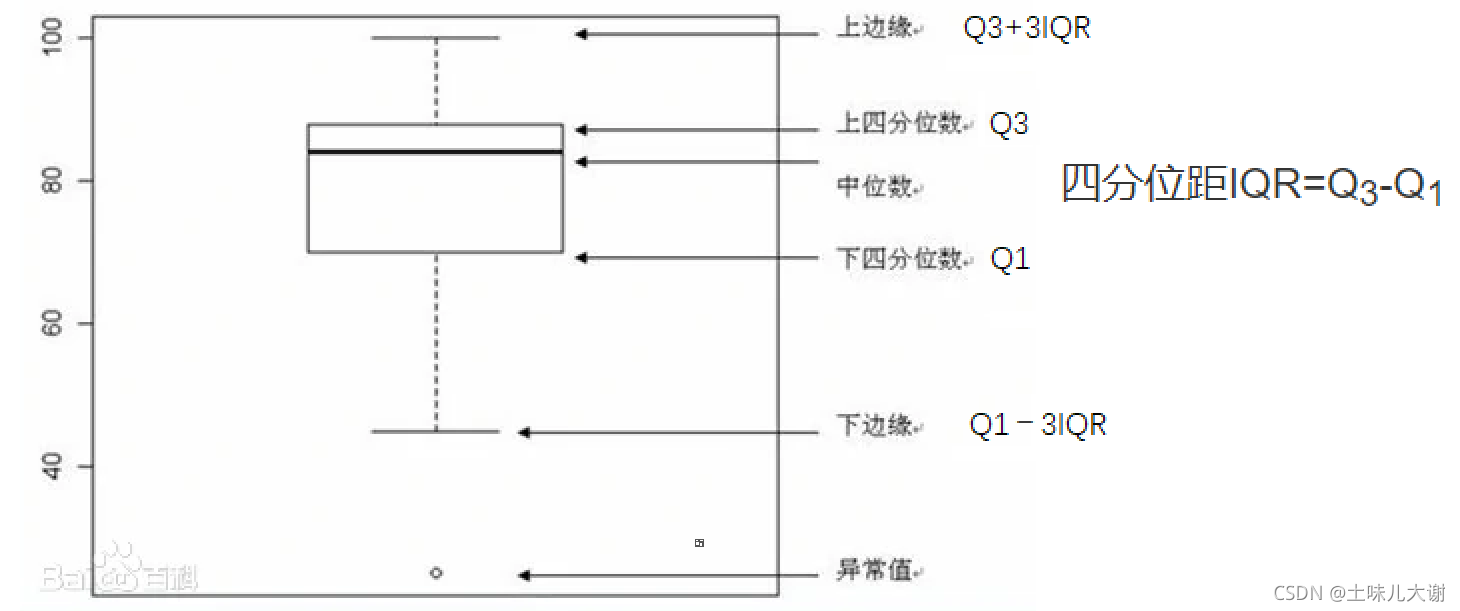 异常值判断:
异常值判断:
- 1、3σ原理(直方图)
- 2、四分位数(箱线图)
2.2 特征预处理
特征预处理常用方法:
- 数值型特征无量纲化
- 数值型特征分箱
- 类别型特征编码
- 特征组合
2.2.1 数值型特征无量纲化
无量纲化使不同规格的数据转换到同一规格。常见的无量纲化方法有标准化,区间缩放法,正则化。
2.2.1.1 标准化
标准化是按照数据的列进行处理
标准化的前提:特征服从正态分布,标准化后,其转化为标准正态分布
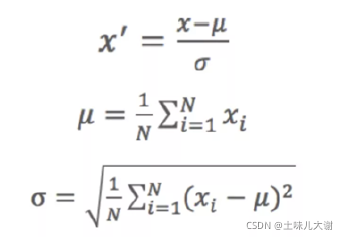
代码实现:
from sklearn.preprocessing import StandardScaler #标准化包
#标准化,返回值为标准化后的数据
std = StandardScaler() #创建模型
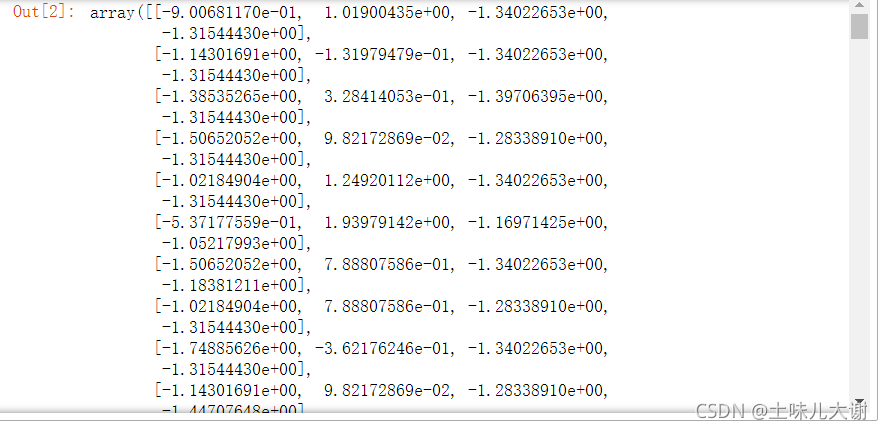
std.fit_transform(iris.data) #标准化
#fit和transform在不同作用下有不同意义,这里是标准化时候的意义
#标准化有以下两个动作:
#第一个动作:fit 均值,标准差求解
#第二个动作:transform 标准化(x-均值)/std
 训练集和测试集如何处理?
训练集和测试集如何处理?
#训练集和测试集情况
std = StandardScaler()
std.fit_transform(训练集)
std.transform(测试集)
测试集不fit的原因:模型追求泛化能力,即对具有同一个规律的数据有很好的预测能力。同一个规律:均值和标准差一样。所以可以用训练集的fit去代替测试集的fit。毕竟训练集的数据数量更多,它的均值和标准差会更接近真实数据的均值和标准差
绘图观察:
fig,ax = plt.subplots(1,2,figsize=(8,4)) #1,2:一行两列;8,4:图的大小;fig:返回一个绘图对象;ax:返回一个子图
#第一个子图,标准化前
pd.Series(iris.data[:,0]).hist(bins=50,color='green',edgecolor='black',grid=False,ax=ax[0])#ax=ax[0]:表示画的是第一个子图;hist:柱状图;bins:条数;edgecolor:边缘颜色;grid:是否需要格子
ax[0].set_title('标准化前',fontsize=12)
ax[0].set_xlabel('花萼长度',fontsize=12)
ax[0].set_ylabel('频率',fontsize=12)
std = StandardScaler() #创建模型
std_data=std.fit_transform(iris.data) #标准化
#第二个子图,标准化后
pd.Series(std_data[:,0]).hist(bins=50,color='green',edgecolor='black',grid=False,ax=ax[1])
ax[1].set_title('标准化后',fontsize=12)
ax[1].set_xlabel('花萼长度',fontsize=12)
ax[1].set_ylabel('频率',fontsize=12)
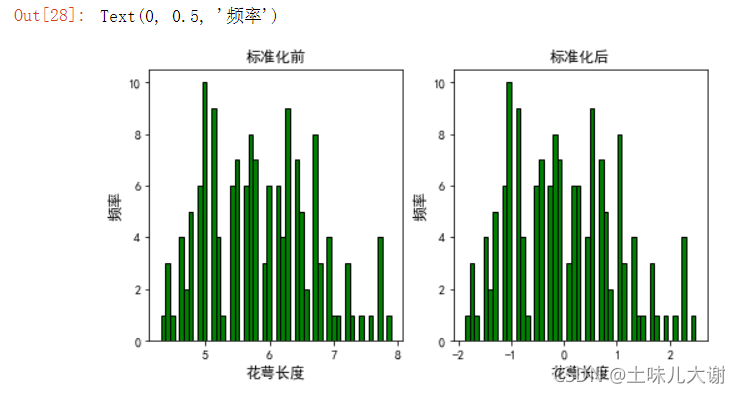 可以观察到:标准化只是把图形移动到原点和缩放,不会改变图形形状和分布
可以观察到:标准化只是把图形移动到原点和缩放,不会改变图形形状和分布
2.2.1.2 区间缩放法(归一化)
区间缩放法利用了边界值信息,将特征的取值区间缩放到某个特征的范围,例如[0,1]等。常见的一种是利用两个最值进行缩放
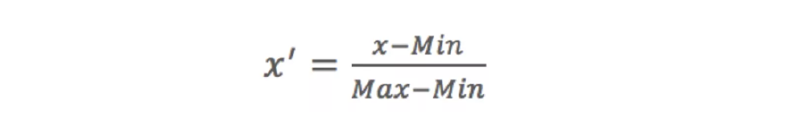
区间缩放也是按照列进行处理
代码实现:
from sklearn.preprocessing import MinMaxScaler
#区间缩放,默认值为缩放到[0, 1]区间的数据
MinMaxScaler().fit_transform(iris.data)
#fit和transform要看对象是什么再确定意义是什么
#比如这里的fit:求最小值和最大值
#transform:就是上面的公式
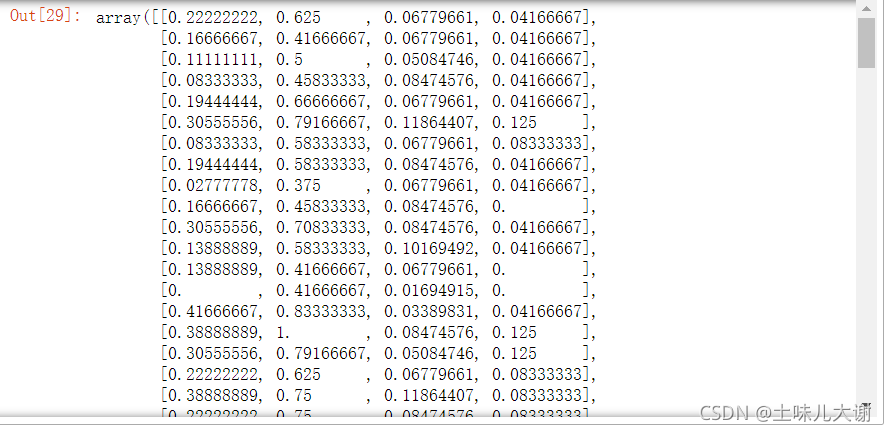
绘图观察:
fig,ax = plt.subplots(1,2,figsize=(8,4))
#第一个子图,归一化前
pd.Series(iris.data[:,0]).hist(bins=50,color='green',edgecolor='black',grid=False,ax=ax[0])
ax[0].set_title('归一化前',fontsize=12)
ax[0].set_xlabel('花萼长度',fontsize=12)
ax[0].set_ylabel('频率',fontsize=12)
Min_data=MinMaxScaler().fit_transform(iris.data) #归一化
#第二个子图,归一化后
pd.Series(Min_data[:,0]).hist(bins=50,color='green',edgecolor='black',grid=False,ax=ax[1])
ax[1].set_title('归一化后',fontsize=12)
ax[1].set_xlabel('花萼长度',fontsize=12)
ax[1].set_ylabel('频率',fontsize=12)
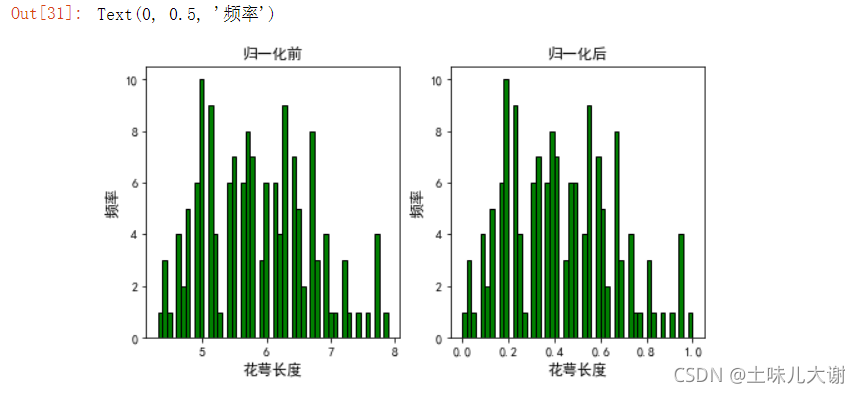
补充:也可以缩放到任意区间,公式如下
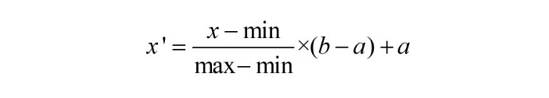
#可以缩放到其他区间 比如缩放到[1,2]这个区间
MinMaxScaler(feature_range=(1,2)).fit_transform(iris.data)
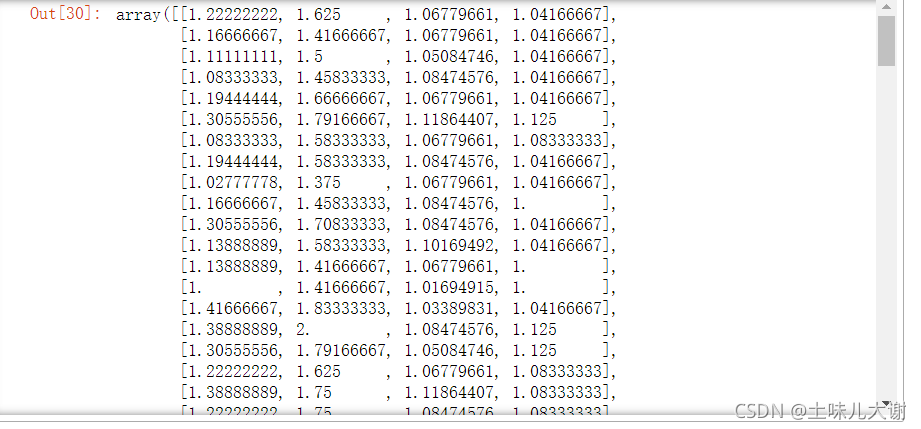
注:区间缩放对异常值的存在非常敏感
2.2.1.3 正则化
- 正则化的过程是将每个样本缩放到单位范数(每个样本的范数为1),是依照特征矩阵的行处理数据
- 其目的在于样本向量在点乘运算或其他核函数计算两个样本之间相似性时,拥有统一的标准,也就是说都转化为“单位向量”。规则为l2的正则化公式如下:
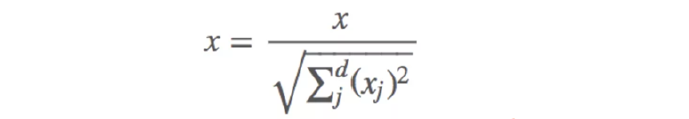
代码实现:
from sklearn.preprocessing import Normalizer
Normalizer(norm='l2').fit_transform(iris.data) #默认为l2
#这里的fit是上面公式分母的操作
#transform就是上面公式的操作了
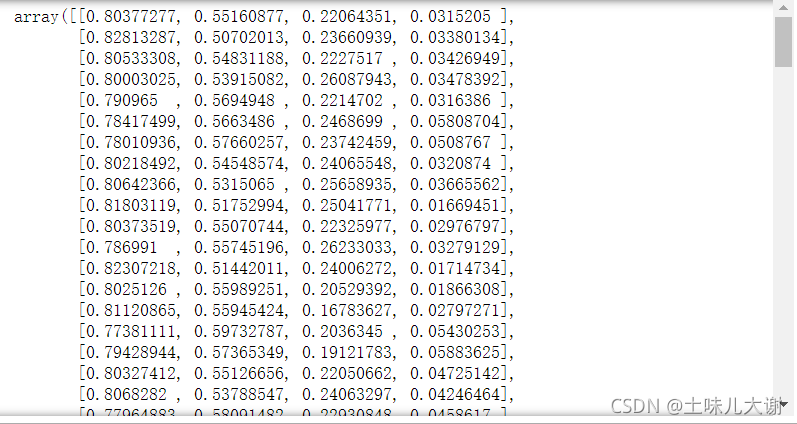
Normalizer(norm='l1').fit_transform(iris.data) #l1正则化
#l1正则化就是上面的公式里面的二次变为1次。上面开了2次根号,l1就不开根号,上面是平方项,l1是绝对值一次方项
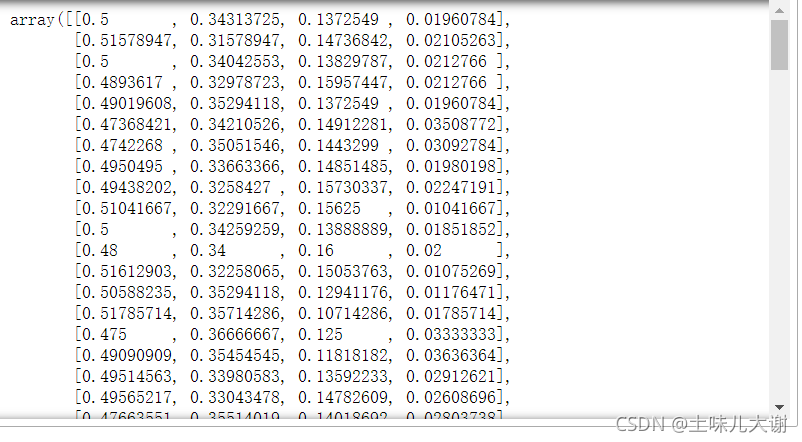
绘图观察:
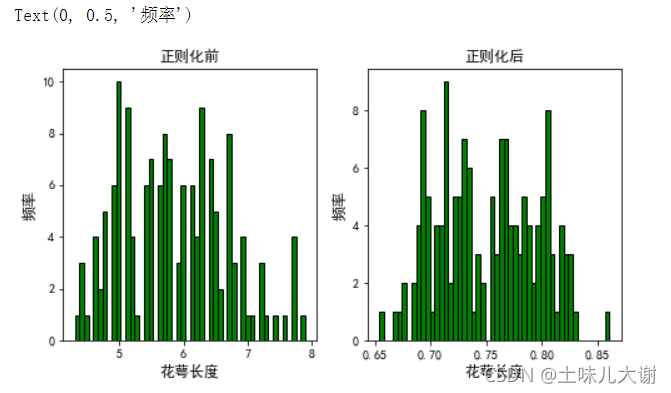
fig,ax = plt.subplots(1,2,figsize=(8,4))
#第一个子图,正则化前
pd.Series(iris.data[:,0]).hist(bins=50,color='green',edgecolor='black',grid=False,ax=ax[0])
ax[0].set_title('正则化前',fontsize=12)
ax[0].set_xlabel('花萼长度',fontsize=12)
ax[0].set_ylabel('频率',fontsize=12)
Normal=Normalizer(norm='l2').fit_transform(iris.data) #默认为l2
#第二个子图,正则化后
pd.Series(Normal[:,0]).hist(bins=50,color='green',edgecolor='black',grid=False,ax=ax[1])
ax[1].set_title('正则化后',fontsize=12)
ax[1].set_xlabel('花萼长度',fontsize=12)
ax[1].set_ylabel('频率',fontsize=12)
2.2.1.4 总结
标准化与归一化的异同
- 相同点:都能去掉由于量纲不同引起的误差;都是一种线性变换,都是对向量x按照比例压缩再进行平移
- 不同点:
- 目的不同,归一化是为了消除纲量压缩到[0,1]区间
- 标准化只是调整特征整体的分布
- 归一化与最大,最小值有关
- 标准化与均值,标准差有关
- 归一化输出在[0,1]之间,标准化无限制
标准化与归一化如何选择
- 如果对输出结果范围有要求,用归一化
- 如果数据较为稳定,不存在极端的最大最小值,用归一化
- 如果数据存在异常值和较多噪音,用标准化,可以间接通过中心化避免异常值和极端值的影响
归一化与标准化常见应用场景
- 在分类、聚类算法中,需要使用距离来度量相似性的时候或者使用PCA技术进行降维的时候,标准化表现更好
- 在不涉及距离度量、协方差计算、数据不符合正态分布的时候,可以使用归一化方法:比如图像处理中,将RGB图像转换为灰度图像后将
其值限定在[0,1]的范围- 基于树的方法不需要进行特征的归一化:例如随机森林,bagging与boosting等方法
- 如果是基于参数的模型或者基于距离的模型,因为需要对参数或者距离进行计算,都需要进行归一化
- 建议优先使用标准化,对于输出有要求时再尝试别的方法
需要掌握↓
无量纲化:标准化,归一化,正则化
1、为什么做
2、如何做的
3、产生什么效果
2.3 数值型特征分箱
离散化(分箱)是数值型特征非常重要的一个处理,其实就是要将数值型数据转化成类别型数据。连续值的取值空间可能是无穷的,为了便于表示和在模型中处理,需要对连续值特征进行离散化处理
2.3.1 无监督分箱法
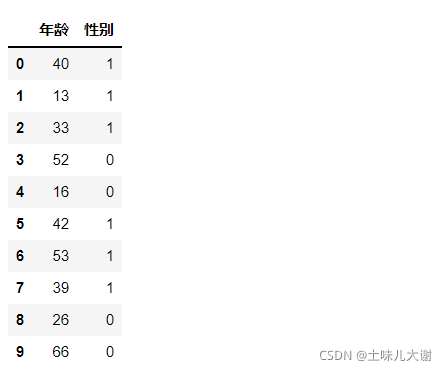
# 创建一组数据来实践各种分箱方法
df = pd.DataFrame([[40,1],[13,1],[33,1],[52,0],[16,0],[42,1],[53,1],[39,1],[26,0],[66,0]],columns=['年龄','性别'])
df
2.3.1.1 自定义分箱
指根据业务经验或者常识等自行设定划分的区间,然后将原始数据归类到各个区间中
bins=[0,20,40,60,80] #按照区间分箱
df['自定义分箱']=pd.cut(df['年龄'],bins=bins,labels=['少年','青年','壮年','老年'])
df
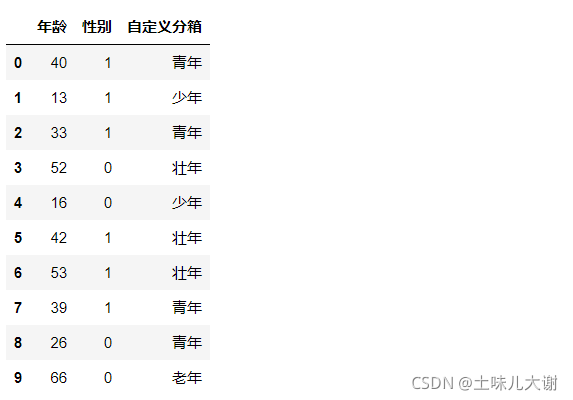
2.3.1.2 等距分箱
按照相同宽度将数据分成几等份。从最小值到最大值之间,均分为 N 等份,缺点是受到异常值的影响比较
大
df['等距分箱'] = pd.cut(df['年龄'],3)
df
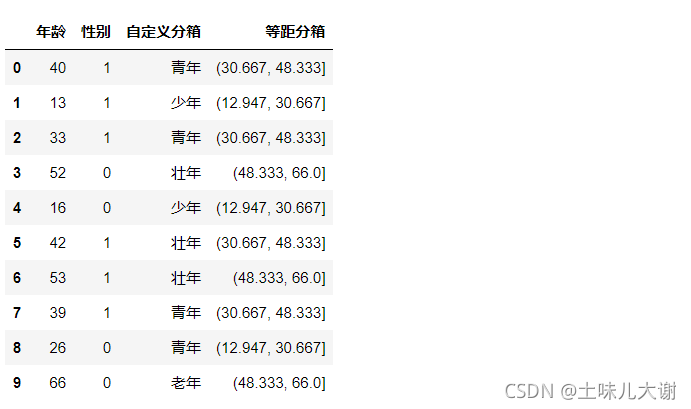
2.3.1.3 等频分箱
将数据分成几等份,每等份数据里面的个数是一样
df['等频分箱'] = pd.qcut(df['年龄'],3)
df
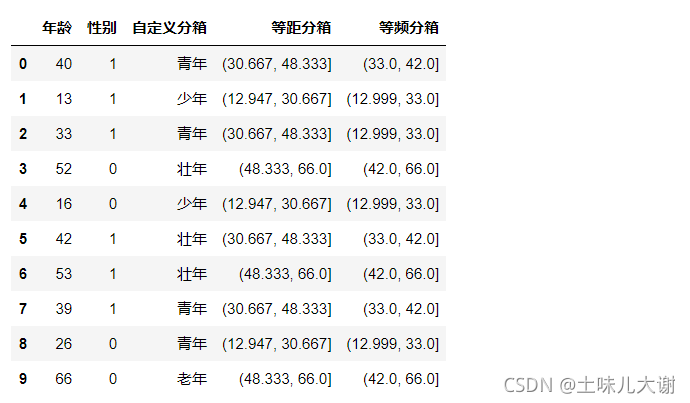
df['等频分箱'].value_counts() #统计分箱后的结果

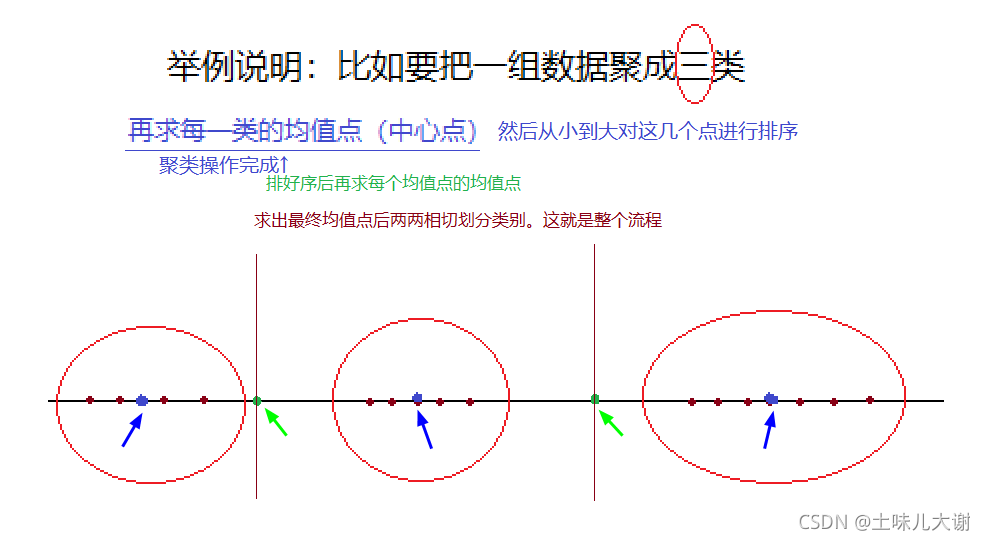
2.3.1.4 聚类分箱(未完成)
基于k均值聚类的分箱,将观测值聚为k类
代码实现:
data=df['年龄'].values
data#观察结果是一个一维数组,但是模型里面得用二维数组,所以用data.reshape(-1,1)这行代表把一维数组转化为了二维数组

from sklearn.cluster import KMeans
kmodel=KMeans(n_clusters=3) #k为聚成几类
kmodel.fit(data.reshape(-1,1)) #训练模型 变为二维数组后进行聚类,也就是上图红圈操作
c=pd.DataFrame(kmodel.cluster_centers_) #求聚类中心 ;也就是上图蓝点操作
c=c.sort_values(by=0) #排序
w=c.rolling(window=2).mean().iloc[1:] #用滑动窗口求均值的方法求相邻两项求中点,作为边界点;也就是求上图绿点的操作
w=[data.min()-1] +list(w[0]) + [data.max()]#把首末边界点加上;-1是因为若是不减,那最小值取不到
df['聚类分箱'] = pd.cut(data,w)
df
2.3.1.5 二值化
将数值型的特征进行阀值化得到布尔型数据
代码实现:
from sklearn.preprocessing import Binarizer
#二值化,阈值设置为3,小于等于3为0,大于3为1
#返回值为二值化后的数据,只有一个=3,那么所有列会对应同一个阈值
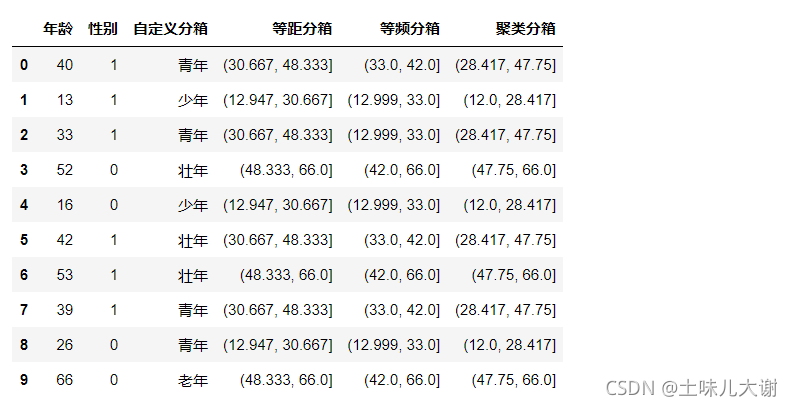
Binarizer(threshold=3).fit_transform(iris.data) #一个阈值对所有的特征
#最常用
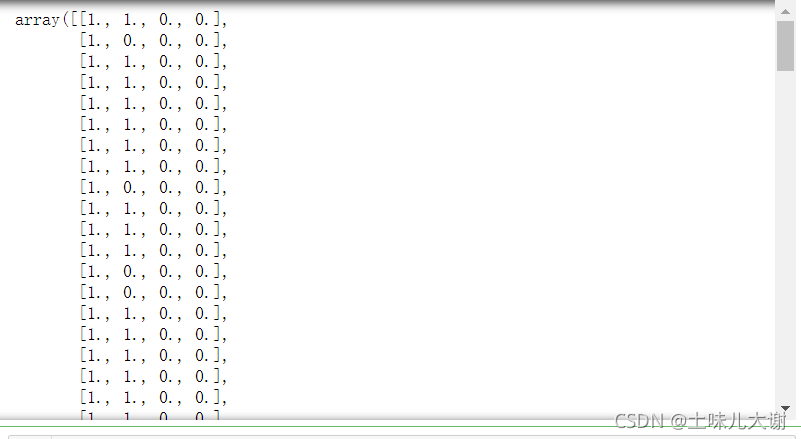
Binarizer(threshold=[5,3,1.5,0.2]).fit_transform(iris.data) #不同的列用不同阈值二值化
2.4 类别特征编码
- 序号编码(LabelEncode):取值有逻辑关系,线性编码
- 独热编码(哑编码):取值独立,非线性编码,特征变多,drop参数,经常和降维、特征选择连用
2.4.1 线性编码(标签编码)
标签编码(LabelEncode):序号编码,对不连续的数字或者文本进行编号,编码值介于0和n-1之间的标签,线性编码方式
代码实现:
from sklearn.preprocessing import LabelEncoder
#dataframe进行编码
import pandas as pd
df=pd.DataFrame([['a','青年'],['b','中年'],['c','老年']],columns=['X','Y'])
df

le = LabelEncoder()
for col in df.columns:
df[col]=le.fit_transform(df[col]) #每一列单独处理 Unicode编码顺序
print(col,le.classes_) #查看编码顺序
df

2.4.2 独热编码
哑编码,设置一个个数与类型数量相同的全0数组,每一位对应一个类型,如该位为1,该数字表示该类型,非线性编码方式
2.4.2.1 get_dummies
import pandas as pd
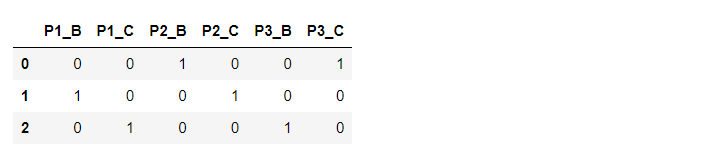
list2=[['A', 'B', 'C'], ['B', 'C', 'A'], ['C', 'A', 'B']]
df1=pd.DataFrame(list2,columns=['P1','P2','P3'])
df1

pd.get_dummies(df1,prefix=['P1','P2','P3'])#prefix列名加一个前缀
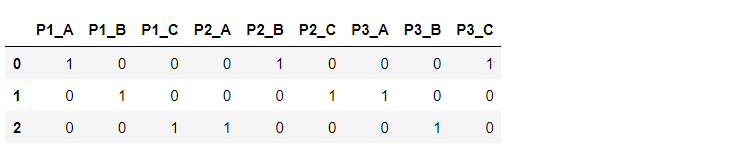
#因为有一列是冗余的,所以要删掉,这里我们删掉第一列(其实删掉哪一列都行,反正要删一列,习惯性删第一列)
pd.get_dummies(df1,prefix=['P1','P2','P3'],drop_first=True) #丢掉第一列
2.4.2.2 OneHotEncoder
代码实现:
from sklearn.preprocessing import OneHotEncoder
list2=[['A', 'B', 'C'], ['B', 'C', 'A'], ['C', 'A', 'B']]
One_hot=OneHotEncoder() #创建模型
One_hot.fit_transform(list2) #稀疏矩阵的形式存储,很多模型支持稀疏矩阵


OneHotEncoder(drop='first').fit_transform(list2) #drop参数丢掉一列
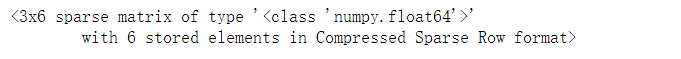

2.5 统计变换
2.5.1 Log变换
log变换通常用来创建单调的数据变换。它的主要作用在于帮助稳定方差,始终保持分布接近于正态分布并使得数据与分布的平均值无关
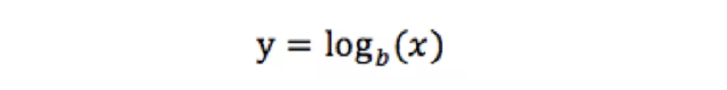
当数据倾斜分布时,Log变换是很有用的,因为Log变换倾向于拉伸那些落在较低的幅度范围内自变量值的范围,倾向于压缩或减少更高幅度范围内的自变量值的范围,从而使得倾斜分布尽可能的接近正态分布
代码实现:
import pandas as pd
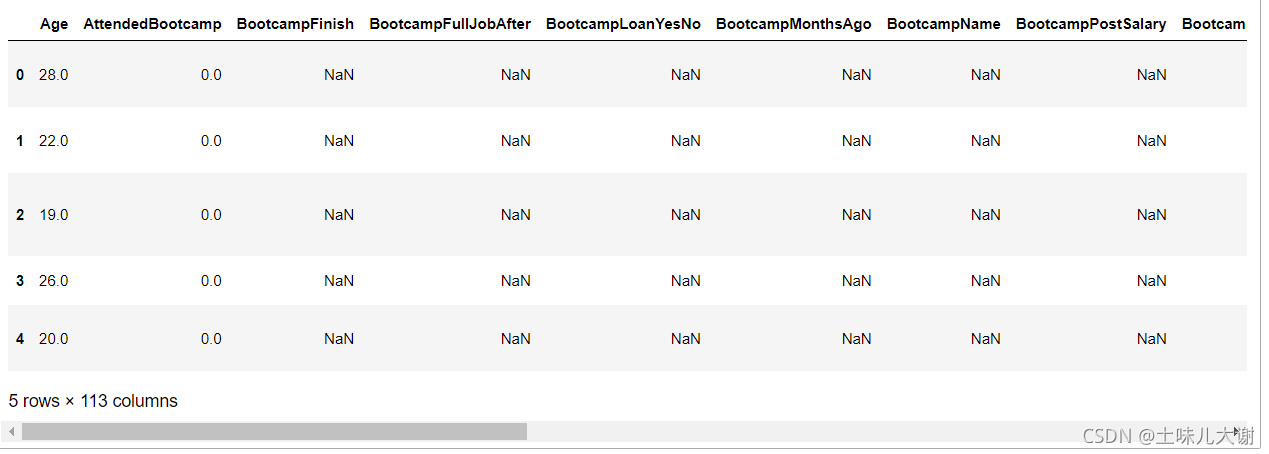
#数据集:freeCodeCamp 做了一个名为coder-survey的调研,以了解成年人学写代码的状况
data = pd.read_csv('2016-new-coder-survey.csv')
data.head()
绘图观察分布:
fig, ax = plt.subplots()
data['Income'].hist(bins=30, color='green',
edgecolor='black', grid=False)
ax.set_title('收入柱状图', fontsize=12)
ax.set_xlabel('收入', fontsize=12)
ax.set_ylabel('频数', fontsize=12)
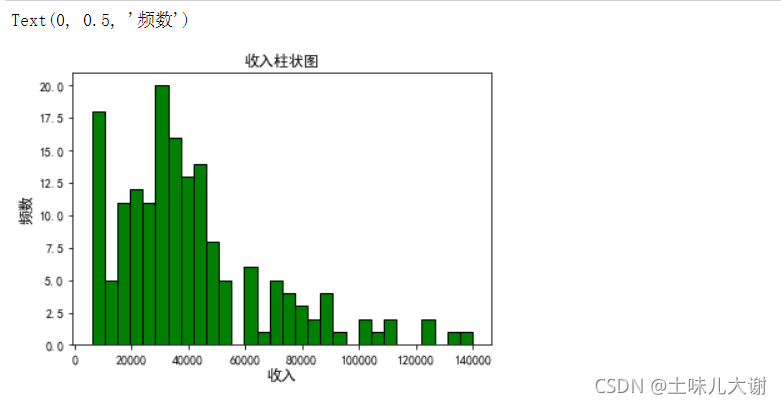
data['Income_log'] = np.log((1+ data['Income']))#log变换,+1是为了防止负数
income_log_mean = np.round(np.mean(data['Income_log']), 2) #取完log后的均值
fig, ax = plt.subplots()
data['Income_log'].hist(bins=30, color='green',
edgecolor='black', grid=False)
plt.axvline(income_log_mean, color='r')
ax.set_title('收入柱状图', fontsize=12)
ax.set_xlabel('收入', fontsize=12)
ax.set_ylabel('频数', fontsize=12);
2.5.2 Box-Cox变换
Box-Cox变换是统计建模中常用的一种数据变换,用于连续的响应变量不满足正态分布的情况。该函数有一个前提条件,即数值型值必须先变换为正数。Box-Cox变换之目标有两个,一个是变换后,可以一定程度上减小不可观测的误差和预测变量的相关性。第二个是用这个变换来使得因变量获得一些性质,比如在时间序列分析中的平稳性,或者使得因变量分布为正态分布

代码实现:
import scipy.stats as spstats
# 从数据分布中移除非零值
income = np.array(data['Income'])
income_clean = income[~np.isnan(income)]#去掉空值为null的
# 计算最佳λ值
l, opt_lambda = spstats.boxcox(income_clean)
print('Optimal lambda value:', opt_lambda)
# 进行Box-Cox变换
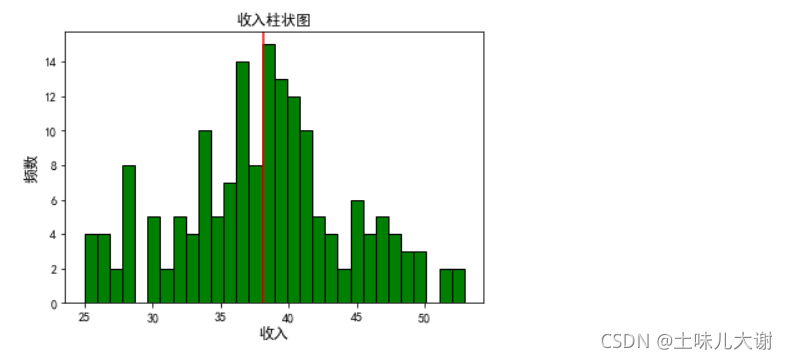
data['Income_boxcox_lambda_opt'] = spstats.boxcox(data['Income'],lmbda=opt_lambda)#变换后得到最佳λ值

绘图观察:
income_boxcox_mean = np.mean(data['Income_boxcox_lambda_opt'])#经过boxcox变换后的均值
fig, ax = plt.subplots()
data['Income_boxcox_lambda_opt'].hist(bins=30,color='green', edgecolor='black', grid=False)
plt.axvline(income_boxcox_mean, color='r')
ax.set_title('收入柱状图', fontsize=12)
ax.set_xlabel('收入', fontsize=12)
ax.set_ylabel('频数', fontsize=12);
2.6 特征组合(特征交叉)
- 是一种合成特征的方法,可以在多维特征数据集上,进行很好的非线性特征拟合,从而提高模型预测的效果
- 用来解决欠拟合问题
2.6.1 连续特征交叉
- 可以通过多项式特征变换实现特征组合
- 4个特征,度为2的多项式转换公式如下
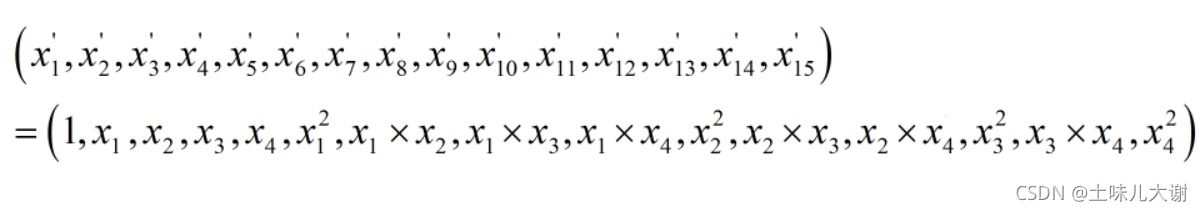
代码实现:
iris.data.shape#鸢尾花数据集为例
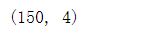
from sklearn.preprocessing import PolynomialFeatures
PolynomialFeatures(degree=2).fit_transform(iris.data).shape
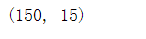
#表示去掉平方项,interaction_only=True:只保留交叉项
PolynomialFeatures(degree=2,interaction_only=True).fit_transform(iris.data).shape
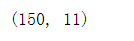
#include_bias=False:把偏置项(常数项)去掉
PolynomialFeatures(degree=2,interaction_only=True,include_bias=False).fit_transform(iris.data).shape
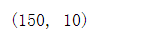
2.6.2 离散特征交叉
- 通过笛卡尔积实现特征交叉
- 比如属性A(年龄)有三个特征(青年,中年,老年),属性B(性别)有两个特征(男,女),笛卡尔积后就有六个组合特征,然后用one hot 给新的特征编码
代码实现:
df = pd.DataFrame([['青年','男'],['中年','女'],['老年','男'],['老年','女']],columns=['年龄','性别'])
df

df1=pd.DataFrame(df['年龄'].unique(),columns=['年龄'])
df1['key']=1
df2=pd.DataFrame(df['性别'].unique(),columns=['性别'])
df2['key']=1
df_12=pd.merge(df1,df2,on='key')
df_12['年龄-性别']=df_12['年龄']+df_12['性别']
df_12

from sklearn.preprocessing import OneHotEncoder
OneHot=OneHotEncoder(drop='first')
OneHot.fit(df_12['年龄-性别'].values.reshape(-1,1))
OneHot.transform(df['年龄-性别'].values.reshape(-1,1)).toarray()

三、特征构造
特征构造指从现有的数据中构造额外特征,这些特征通常分布在多张相关的表中。特征构造需要从数据中提取相关信息并将其存入单张表格中,然后用来训练机器学习模型
3.1 时间特征构造
3.1.1 连续值时间特征
- 持续时间:单页浏览时长
- 间隔时间:上次购买/点击离现在的时长;产品上线到现在经过的时长
代码实现:
#构造两个时间序列
time_list = [['2019-01-01 01:22:26', '2019-02-02 04:34:52', '2019-03-03 06:16:40',
'2019-04-04 08:11:38', '2019-05-05 10:52:39', '2019-06-06 12:06:25'],
['2019-07-07 14:05:25', '2019-08-08 16:51:33', '2019-09-09 18:28:28',
'2019-10-10 20:55:12', '2019-11-11 22:55:12', '2019-12-12 00:55:12']]
df = pd.DataFrame(time_list).T
df.columns=['t1','t2'] #列名
df

#类型为object类型,需要转换为时间类型
df['t1']=pd.to_datetime(df['t1'])
df['t2']=pd.to_datetime(df['t2'])
df['持续时间']=df['t2']-df['t1'] #时间差,得到有单位的时间
df['持续时间']

pd.Timedelta(‘02:05:00’).seconds/3600 #Timedelta对象有属性:weeks、days、seconds、milliseconds、microseconds和nanoseconds等
#pd.Timedelta(x).days得到天数;pd.Timedelta(x).seconds/3600/24 得到后面时间的天数
df['持续时间'].apply(lambda x:pd.Timedelta(x).days+pd.Timedelta(x).seconds/3600/24)

3.1.2 离散值时间特征
import pandas as pd
date_time_str_list = [
'2019-01-01 01:22:26', '2019-02-02 04:34:52', '2019-03-03 06:16:40',
'2019-04-04 08:11:38', '2019-05-05 10:52:39', '2019-06-06 12:06:25',
'2019-07-07 14:05:25', '2019-08-08 16:51:33', '2019-09-09 18:28:28',
'2019-10-10 20:55:12', '2019-11-11 22:55:12', '2019-12-12 00:55:12',
]
df = pd.DataFrame({'时间': date_time_str_list})
df['时间'] = pd.to_datetime(df['时间'])
df

3.1.2.1 时间特征拆解
- 时间特征拆解:年,月,日,时,分,秒,星期几,一年中的第几天,一年中的第几个周,一天中哪个时间段:凌晨、早晨、上午、中午、下午、傍晚、晚上、深夜,一年中的哪个季度
代码实现:
# 年份
df['年']=df['时间'].dt.year
# 月份
df['月']=df['时间'].dt.month
# 日 一个月的第几天
df['日']=df['时间'].dt.day
# 小时 一天的第几个小时
df['时']=df['时间'].dt.hour
# 分钟 一个小时的第几分钟
df['分']=df['时间'].dt.minute
# 秒数 一个分钟内的秒数
df['秒']=df['时间'].dt.second
# 一天中的第几分钟
df['一天中的第几分钟']=df['时间'].apply(lambda x: x.minute + x.hour*60)
# 星期几,一周的第几天
df['星期几']=df['时间'].apply(lambda x: x.dayofweek+1)
# 一年中的第几天
df['一年中的第几天']=df['时间'].dt.dayofyear
# 一年中的第几周
df['一年中的第几周']=df['时间'].dt.week
# 季度
df['一年中的第几个季度']=df['时间'].dt.quarter
# 一天中哪个时间段:凌晨、早晨、上午、中午、下午、傍晚、晚上、深夜;
period_dict ={
23: '深夜', 0: '深夜', 1: '深夜',
2: '凌晨', 3: '凌晨', 4: '凌晨',
5: '早晨', 6: '早晨', 7: '早晨',
8: '上午', 9: '上午', 10: '上午', 11: '上午',
12: '中午', 13: '中午',
14: '下午', 15: '下午', 16: '下午', 17: '下午',
18: '傍晚',
19: '晚上', 20: '晚上', 21: '晚上', 22: '晚上',
}
df['时间段']=df['时'].map(period_dict)
# 自定义季度
season_dict = {
1: '春季', 2: '春季', 3: '春季',
4: '夏季', 5: '夏季', 6: '夏季',
7: '秋季', 8: '秋季', 9: '秋季',
10: '冬季', 11: '冬季', 12: '冬季',
}
df['季节']=df['月'].map(season_dict)
df
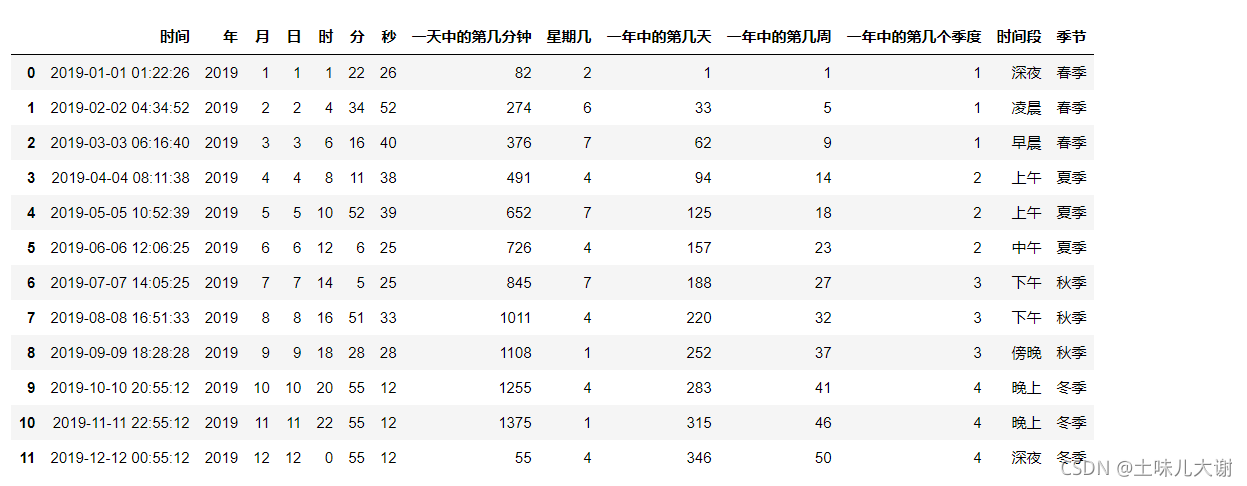
df.set_index('时间').index.year #若时间是索引的提取方式
3.1.2.2 时间特征判断(得到布尔型数据)
- 时间特征判断:是否闰年,是否月初,是否月末,是否季节初,是否季节末,是否年初,是否年尾,是否周末,是否公共假期,是否营业
时间,两个时间间隔之间是否包含节假日/特殊日期
代码实现:
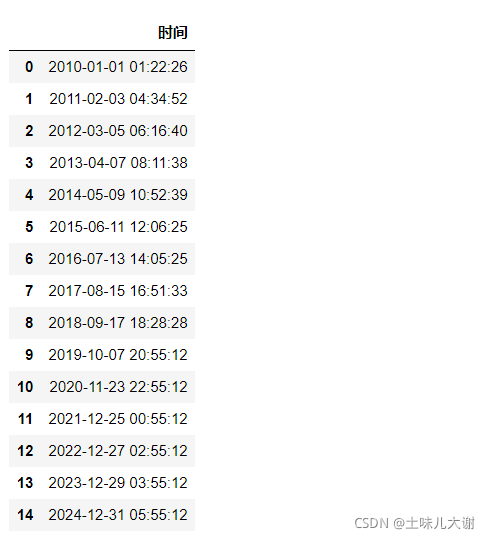
date_time_str_list = [
'2010-01-01 01:22:26', '2011-02-03 04:34:52', '2012-03-05 06:16:40',
'2013-04-07 08:11:38', '2014-05-09 10:52:39', '2015-06-11 12:06:25',
'2016-07-13 14:05:25', '2017-08-15 16:51:33', '2018-09-17 18:28:28',
'2019-10-07 20:55:12', '2020-11-23 22:55:12', '2021-12-25 00:55:12',
'2022-12-27 02:55:12', '2023-12-29 03:55:12', '2024-12-31 05:55:12',
]
df = pd.DataFrame({'时间': date_time_str_list})
df['时间'] = df['时间'].apply(lambda x: pd.Timestamp(x))
df
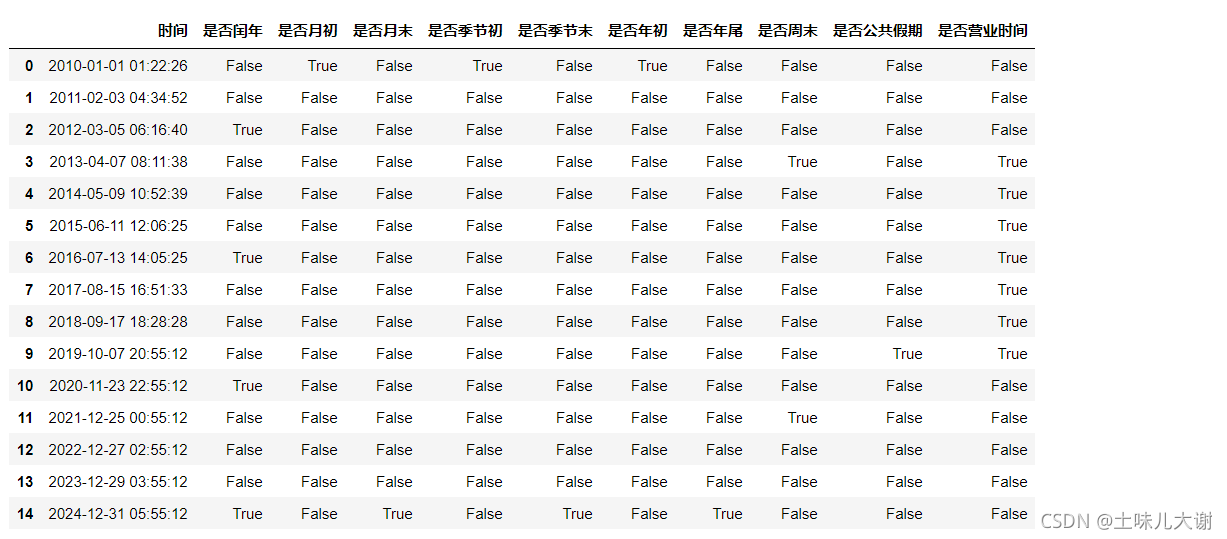
# 是否闰年
df['是否闰年'] = df['时间'].dt.is_leap_year
# 是否月初,是否是一个月的第一天
df['是否月初'] = df['时间'].apply(lambda x: x.is_month_start)
# 是否月末,是否是一个月的最后一天
df['是否月末'] = df['时间'].apply(lambda x: x.is_month_end)
# 是否季节初
df['是否季节初'] = df['时间'].apply(lambda x: x.is_quarter_start)
# 是否季节末
df['是否季节末'] = df['时间'].apply(lambda x: x.is_quarter_end)
# 是否年初 每年的第一天
df['是否年初'] = df['时间'].apply(lambda x: x.is_year_start)
# 是否年尾 每年的最后一天
df['是否年尾'] = df['时间'].apply(lambda x: x.is_year_end)
# 是否周末
df['是否周末'] = df['时间'].apply(lambda x: True if x.dayofweek in [5, 6] else False)
# 是否公共假期
public_vacation_list = [
'20190101', '20190102', '20190204', '20190205', '20190206',
'20190207', '20190208', '20190209', '20190210', '20190405',
'20190406', '20190407', '20190501', '20190502', '20190503',
'20190504', '20190607', '20190608', '20190609', '20190913',
'20190914', '20190915', '20191001', '20191002', '20191003',
'20191004', '20191005', '20191006', '20191007',
] # 此处未罗列所有公共假期
df['日期'] = df['时间'].apply(lambda x: x.strftime('%Y%m%d')) #strftime函数把标准时间转换为咱想要的时间格式
df['是否公共假期'] = df['日期'].apply(lambda x: True if x in public_vacation_list else False)
# 是否营业时间
df['是否营业时间'] = False
df['小时']=df['时间'].apply(lambda x: x.hour)
df.loc[((df['小时'] >= 8) & (df['小时'] < 22)), '是否营业时间'] = True
df.drop(['日期', '小时'], axis=1, inplace=True)
df
3.2 时间序列特征构造
按固定时间长度把时间序列划分成多个时间窗,然后构造每个时间窗的特征
3.2.1 时间序列聚合特征
- 聚合:把多个时间段的值做一种运算
- 平均值:历史销售量平均值、最近N天销售量平均值
- 最小值:历史销售量最小值、最近N天销售量最小值
- 最大值:历史销售量最大值、最近N天销售量最大值
- 扩散值:分布的扩散性,如标准差、平均绝对偏差或四分位差,可以反映测量的整体变化趋势
- 离散系数值:离散系数是策略数据离散程度的相对统计量,主要用于比较不同样本数据的离散程度
- 分布性:时间序列测量的边缘分布的高阶特效估计(如偏态系数或峰态系数),或者更进一步对命名分布进行统计测试(如标准或统一性),在某些情况下比较有预测力
代码实现:
# 加载洗发水销售数据集,每个月的
df = pd.read_csv('shampoo-sales.csv')
df

# 平均值
mean_v = df['Sales'].mean()
print('mean: {}'.format(mean_v))
# 最小值
min_v = df['Sales'].min()
print('min: {}'.format(min_v))
# 最大值
max_v = df['Sales'].max()
print('max: {}'.format(max_v))
# 扩散值:标准差
std_v = df['Sales'].std()
print('std: {}'.format(std_v))
# 扩散值:平均绝对偏差
mad_v = df['Sales'].mad()
print('mad: {}'.format(mad_v))
# 扩散值:四分位差
q1 = df['Sales'].quantile(q=0.25) #下四分位
q3 = df['Sales'].quantile(q=0.75) #上四分位
irq = q3 - q1 #四分位距
print('q1={}, q3={}, irq={}'.format(q1, q3, irq))
# 离散系数
variation_v = std_v/mean_v
print('variation: {}'.format(variation_v))
# 分布性:偏态系数
skew_v = df['Sales'].skew()
print('skew: {}'.format(skew_v))
# 分布性:峰态系数
kurt_v = df['Sales'].kurt()
print('kurt: {}'.format(kurt_v))

3.2.2 时间序列历史特征
- 前一(或n)个窗口的取值:昨天、前天和3天前的销售量
- 周期性时间序列前一(或n)周期的前一(或n)个窗口的取值:写字楼楼下的快餐店的销售量一般具有周期性,周期长度为7天,7天前和14天前的销售量
代码实现:
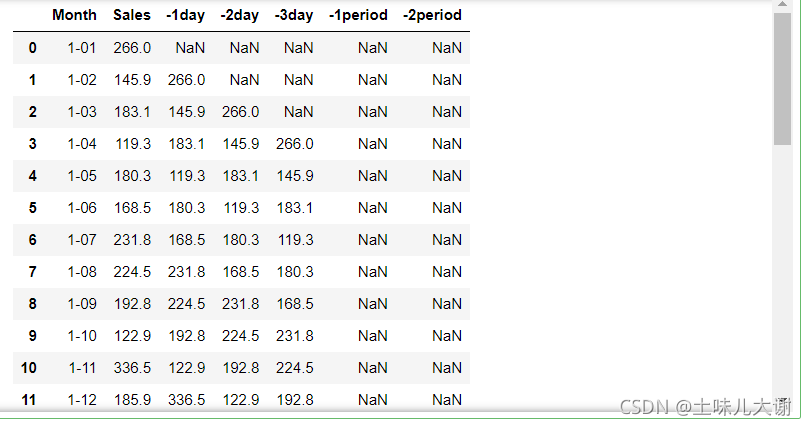
# 加载洗发水销售数据集
df = pd.read_csv('shampoo-sales.csv')
df['-1day'] = df['Sales'].shift(1)#往下移动1天
df['-2day'] = df['Sales'].shift(2)
df['-3day'] = df['Sales'].shift(3)
df['-1period'] = df['Sales'].shift(1*12)#移动1年
df['-2period'] = df['Sales'].shift(2*12)
df
3.2.3 时间序列趋势特征
- 趋势特征 :趋势特征可以刻画时间序列的变化趋势
- 窗口差异值特征:一个窗口到下一个窗口的差异
- 自相关性特征:原时间序列与自身左移一个时间空格(没有重叠的部分被移除)的时间序列相关联
3.2.3.1 趋势特征
代码实现:
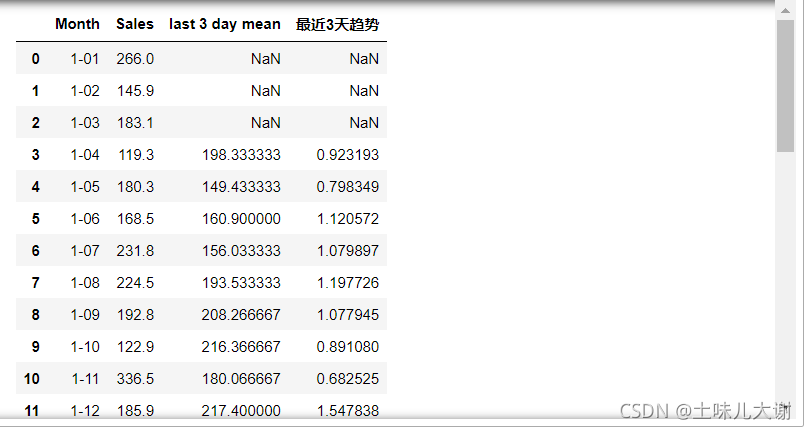
df = pd.read_csv('shampoo-sales.csv')
#↓求最近三天的均值
df['last 3 day mean'] = (df['Sales'].shift(1) + df['Sales'].shift(2) + df['Sales'].shift(3))/3
df['最近3天趋势'] = df['Sales'].shift(1)/df['last 3 day mean']
df
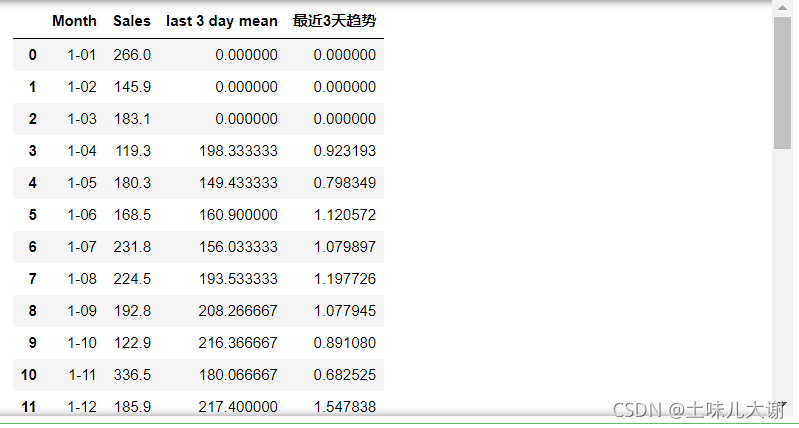
绘图观察:
df1=df.fillna(0) #用0填充空值
df1
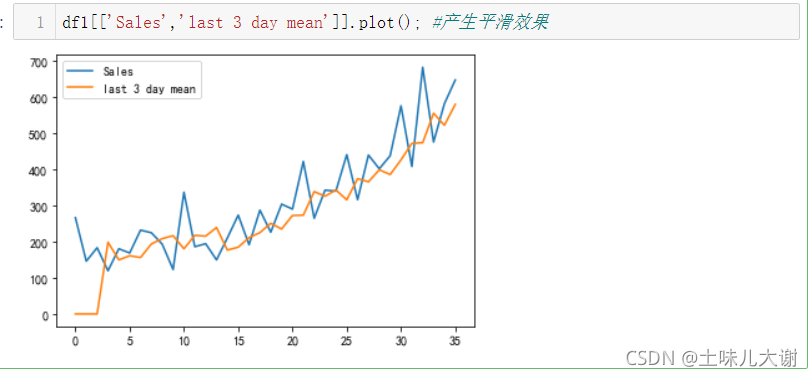
df1[['Sales','last 3 day mean']].plot(); #产生平滑效果
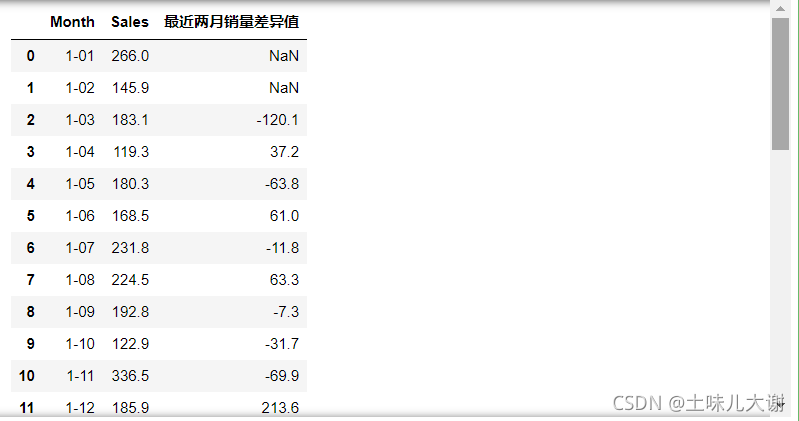
3.2.3.2 窗口差异值特征
df = pd.read_csv('shampoo-sales.csv')
df['最近两月销量差异值'] = df['Sales'].shift(1) - df['Sales'].shift(2)#上个月-下个月
df
3.2.3.3 自相关特征
print('滞后数为1的自相关系数:{}'.format(df['Sales'].autocorr(1)))#往下移动一格求它的相关系数
print('滞后数为2的自相关系数:{}'.format(df['Sales'].autocorr(2)))
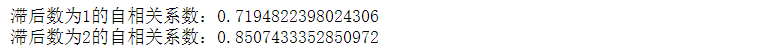
3.3 空间特征构造
- 按经纬度对空间进行划分
- 使用坐标拾取系统获取行政区域信息(类别特征)
- 省份ID/名字
- 城市ID/名字
- 市辖区ID/名字
- 街道ID/名字
- 结合其他地址计算距离
- 例如:计算每个地点至某商业中心的距离
距离类型
- 曼哈顿距离
- 欧式距离
- 球面距离
3.4 用户行为特征构造
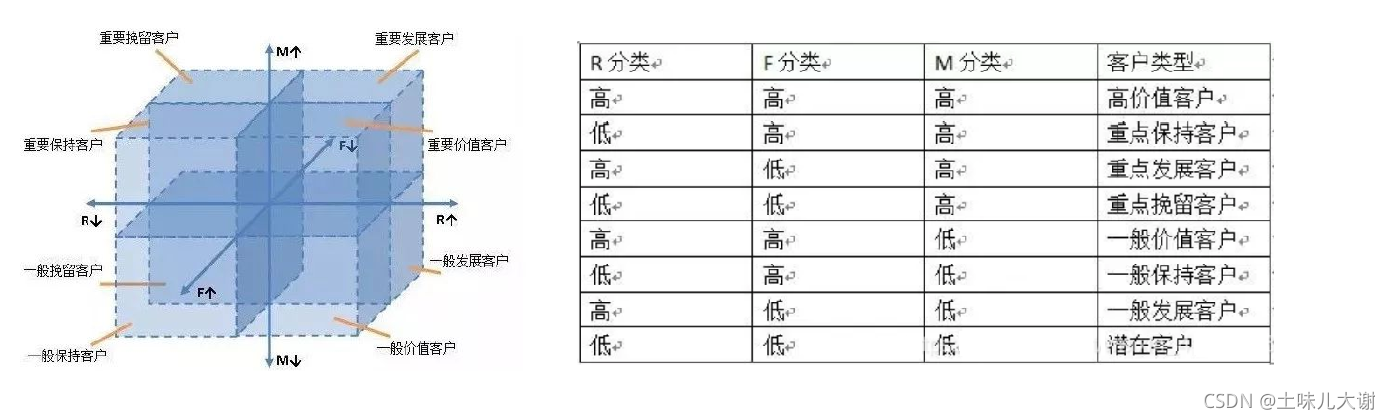
RFM模型:根据客户活跃程度和交易金额的贡献,进行客户价值细分
RFM模型三个指标
- R(Recency)——最近一次消费时间。基于最近一次交易日期计算的得分,距离当前日期越近,得分越高。反映客户交易活跃度
- F(Frequency)——消费频率。基于交易频率计算的得分,交易频率越高,得分越高。反映客户交易活跃度
- M(Monetary)——购买金额。基于交易金额计算的得分,交易金额越高,得分越高。反映客户价值
3.5 文本特征构造
3.5.1 文本统计特征(不常用)
- 文本长度
- 单词个数
- 数字个数
- 字母个数
- 大小写单词个数
- 大小写字母个数
- 标点符号个数
- 特殊字符个数
- 数字占比
- 字母占比
- 特殊字符占比
- 名词个数
- 动词个数
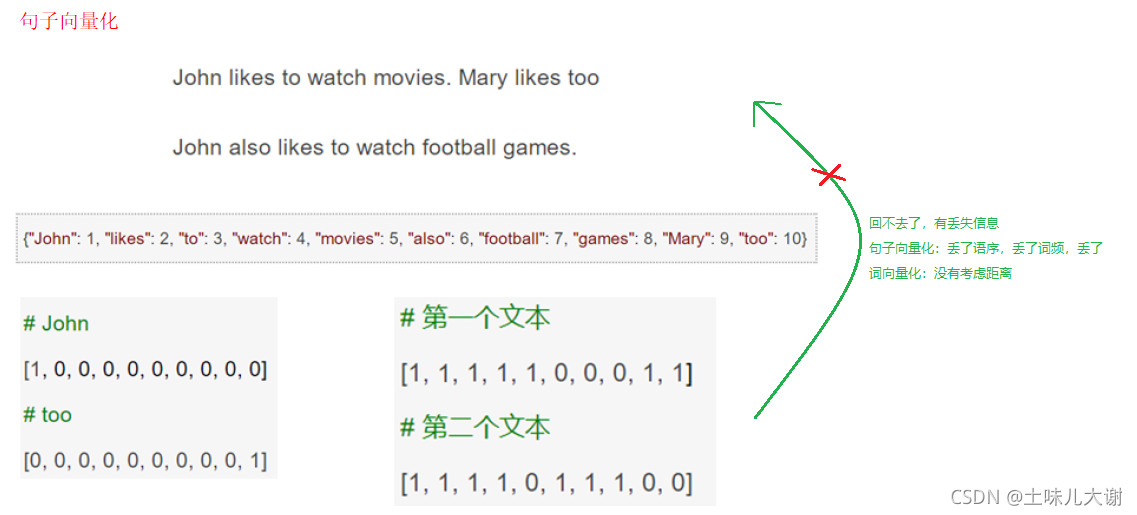
3.5.2 词集模型(SoW)
词集模型( Set Of Words):单词构成的集合,集合中每个元素都只有一个,也即词集中的每个单词都只有一个。把每个词表示为一个很长的向量。这个向量的维度是词表大小,一个维度的值为1,其他元素为0,这个维度就代表了当前的词
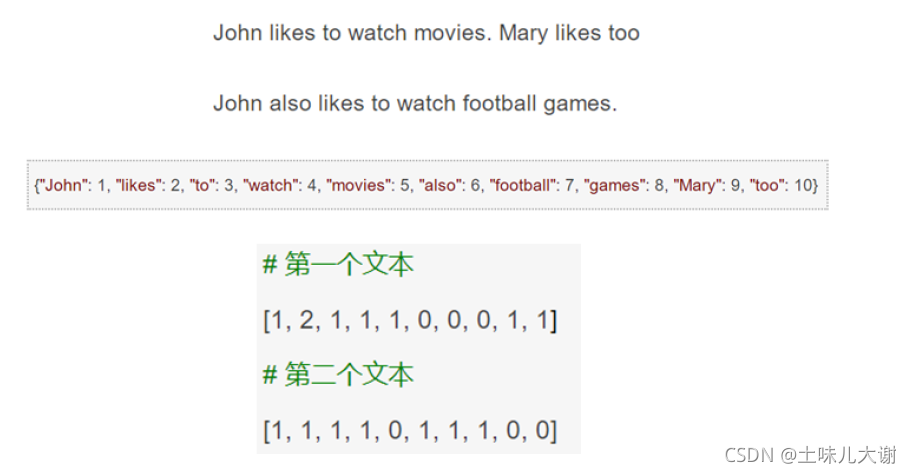
3.5.3 词袋模型(BoW)
词袋模型(Bag Of Words): 统计其出现的次数(频数)
代码实现:
from sklearn.feature_extraction.text import CountVectorizer
#语料库(列表形式↓) 每一行句子为一个样本;词与词之间用空格分开
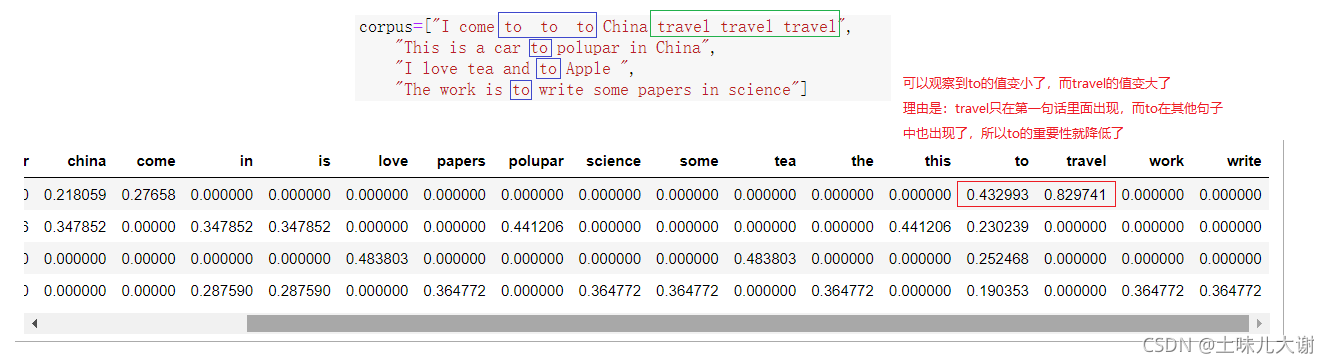
corpus=["I come to to to China travel travel travel",
"This is a car to polupar in China",
"I love tea and to Apple ",
"The work is to write some papers in science"]
vectorizer=CountVectorizer() #创建模型;向量化
vectorizer.fit_transform(corpus) #稀疏矩阵形式进行存储
#这里的fit是拆分词,统计多少个单词,并且给每一个词做一个编码的操作
#transform是对句子做转换,转换为稀疏矩阵的操作;注意:对测试集不做fit操作,只做transform操作

#若想看里面具体数值,用toarray()转化为数组;一般情况下不用转换
#单个字母词去掉,停用词
df1=pd.DataFrame(vectorizer.fit_transform(corpus).toarray(),columns=vectorizer.get_feature_names())
df1


3.5.4 TF-IDF模型
- TF-IDF模型:考虑词的重要度
TF意思是词频(Term Frequency),IDF意思是逆文本频率指数(InverseDocument Frequency) - 字词的重要性随着它在文件中出现的次数成正比增加,但同时会随着它在语料库中出现的频率成反比下降
- 一个词语在一篇文章中出现次数越多, 同时在所有文档中出现次数越少, 越能够代表该文章

#TF-IDF
from sklearn.feature_extraction.text import TfidfVectorizer
corpus=["I come to to to China travel travel travel",
"This is a car to polupar in China",
"I love tea and to Apple ",
"The work is to write some papers in science"]
tfidf = TfidfVectorizer() #创建模型
re = tfidf.fit_transform(corpus)
re

#TF-IDF模型
pd.DataFrame(re.toarray(),columns=tfidf.get_feature_names())
3.5.5 中文文本处理
首先要安装jieba库
在[Win+R → cmd]命令提示符里面输入下面那行代码完成安装
pip install -i https://pypi.tuna.tsinghua.edu.cn/simple --trusted-host pypi.tuna.tsinghua.edu.cn jieba
import jieba #结巴库
jieba.lcut('我喜欢来中国旅游')#分词

' '.join(jieba.lcut('我喜欢来中国旅游'))#用空格分开字符串

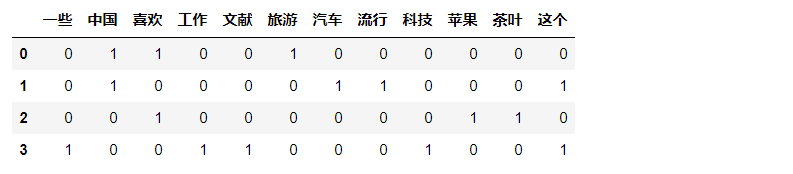
corpus=["我喜欢来中国旅游",
"这个汽车在中国很流行",
"我喜欢茶叶和苹果",
"这个工作是写一些科技文献"]
corpus_jieba=[' '.join(jieba.lcut(sen)) for sen in corpus]#用空格分词
corpus_jieba

vectorizer=CountVectorizer()#建模
pd.DataFrame(vectorizer.fit_transform(corpus_jieba).toarray(),columns=vectorizer.get_feature_names())
3.6 图形特征构造(图形处理领域用的多)
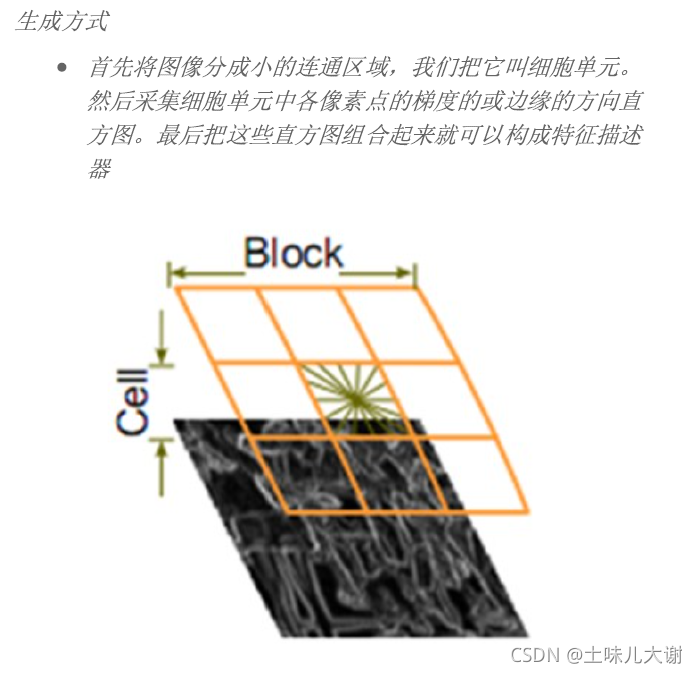
- HOG:方向梯度直方图(Histogram of Oriented Gradient, HOG)特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征
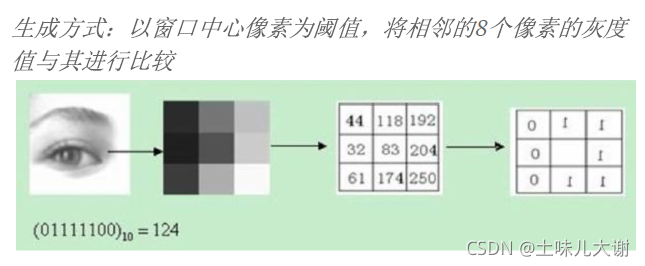
- LBP:局部二值模式(Local Binary Pattern)是一种用来描述图像局部纹理特征的算子;它具有旋转不变性和灰度不变性等显著的优点
- Haar-like:Haar特征分为三类:边缘特征、线性特征、中心特征和对角线特征,组合成特征模板。特征模板内有白色和黑色两种矩形,并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。Haar特征值反映了图像的灰度变化情况
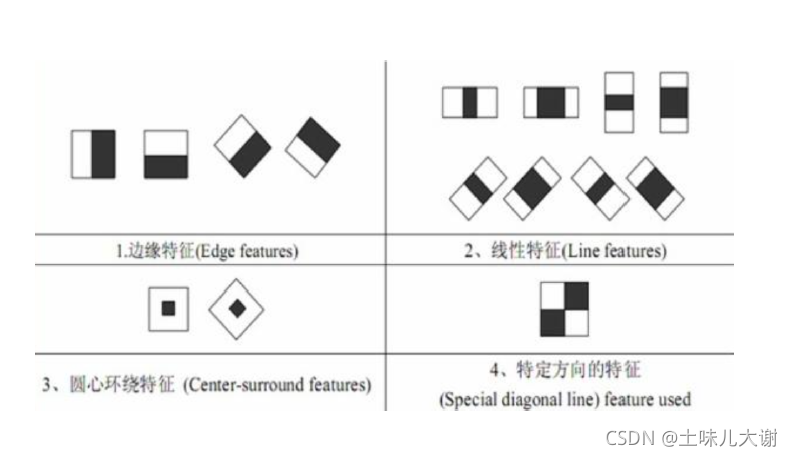
代码实现:
import matplotlib.pyplot as plt
img1 = plt.imread("lena_black.jpg")#灰度图
img1


img2 = plt.imread("lena_cor.jpg")#RGB彩色图
img2.shape


四、特征选择
当数据预处理完成后,我们需要选择有意义的特征输入机器学习的算法和模型进行训练
进行特征选择的原因
- 避免维数灾难:能剔除不相关或冗余的特征,从而达到减少特征个数,提高模型精确度,减少运行时间的目的
- 降低学习任务的难度:选取出真正相关的特征简化模型,协助理解数
据产生的过程
选择特征需要考虑的点
- 特征是否发散:如果一个特征不发散,例如方差接近于0,也就是说样本在这个特征上基本上没有差异,这个特征对于样本的区分并没有什么用
- 特征与目标的相关性:与目标相关性高的特征,应当优先选择
特征选择方法可以分为三种:过滤法、嵌入法和包装法
4.1 过滤法
Filter:过滤法,按照发散性或者相关性对各个特征进行评分,设定阈值或者待选择阈值的个数,选择特征
4.1.1 方差过滤法
使用方差选择法时,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征
代码实现:
from sklearn.datasets import load_iris #导入鸢尾花数据集为例
iris = load_iris()
iris.data
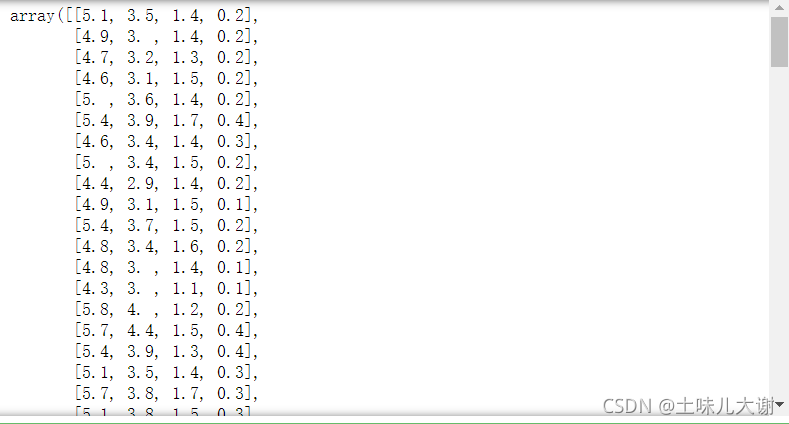
#方差选择法,先要计算各个特征的方差,然后根据阈值,选择方差大于阈值的特征
from sklearn.feature_selection import VarianceThreshold
VarianceThreshold(threshold=0.5).fit_transform(iris.data)#只有方差>0.5才会被选择出来
#这个结果可以观察到选出来的特征没有名字,若特征一多就不容易分辨哪些特征被选择出来了

确定选择特征的字段
data=pd.DataFrame(iris.data,columns=iris.feature_names)
data
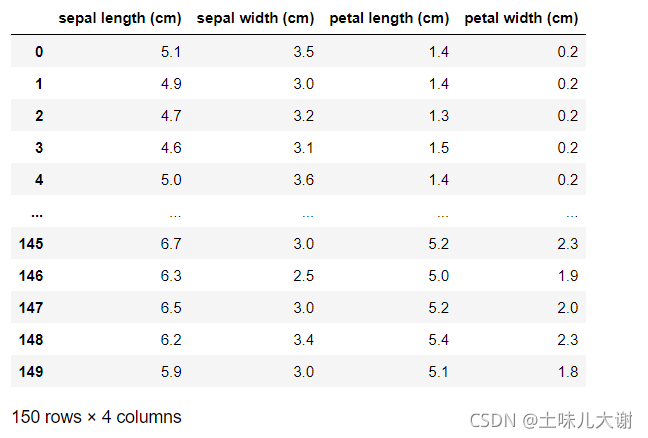
Var=VarianceThreshold(threshold=0.5)
Var.fit_transform(data) #特征选择
Var.get_support() #选择了哪些特征;选择的特征会以True形式标识出来
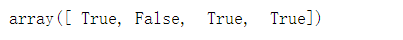
data.columns[Var.get_support()]#查看选择的特征字段名
4.1.2 卡方过滤
- 卡方过滤是专门针对离散型标签(即分类问题)的相关性过滤。卡方检验计算每个非负特征和标签之间的卡方统计量,并依照卡方统计量由高到低为特征排名
- 卡方检验的本质是推测两组数据之间是否相互独立,其检验的原假设是”两组数据之间无关”。卡方检验返回卡方值和P值两个统计量,其中卡方值很难界定有效的范围,而p值,我们一般使用0.01或0.05作为显著性水平,即p值判断的边界
| P值 | ≤0.05或0.01 | >0.05或0.01 |
|---|---|---|
| 数据差异 | 差异不是自然形成的 | 这些差异是很自然的样本误差 |
| 相关性 | 两组数据是相关的 | 两组数据是相互独立的 |
| 原假设 | 拒绝原假设,接收备择假设 | 接受原假设 |
代码实现:
from sklearn.feature_selection import SelectKBest #选择K个最好的
from sklearn.feature_selection import chi2 # 卡方检验
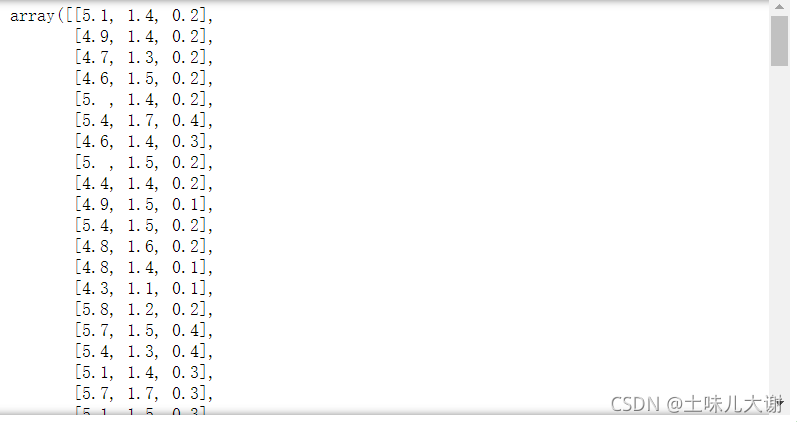
SelectKBest(chi2, k=3).fit_transform(iris.data, iris.target) #选择三个特征,然后数据和标签放进去,每一列都和标签进行相关性的计算,观察独立性后进行特征选择
chi2val, pval = chi2(iris.data, iris.target)#算出卡方值和P值
(pval<0.05).sum() #根据P值确定选择的数量k
4.1.3 F检验法
- F检验,又称ANOVA,方差齐性检验,是用来捕捉每个特征与标签之间的线性关系的过滤方法。它既可以做回归也可以做分类,其中F检验分类(f_classif)用于标签是离散型变量的数据,而F检验回归(f_regression)用于标签是连续型变量的数据
- F检验在数据服从正态分布时效果会非常稳定,因此如果使用F检验过滤,我们会先将数据转换成服从正态分布的方式
代码实现:
#分类f_classif,回归f_regression
from sklearn.feature_selection import f_classif,f_regression
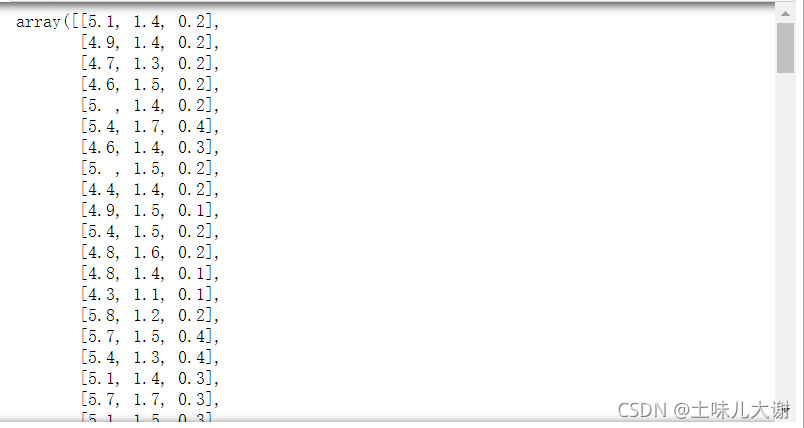
SelectKBest(f_classif, k=3).fit_transform(iris.data, iris.target)
F, pval_f = f_classif(iris.data, iris.target)
pval_f #可以和上面一样选择0.05或0.1来确定k的数量
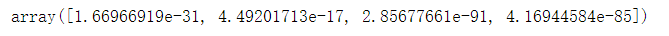
4.1.4 互信息法
- 经典的互信息也是评价定性自变量对定性因变量的相关性的。互信息是已知一个变量,另外一个变量减少的信息量,在概率论和信息论中,互信息是两个随机变量的间相互依赖性的度量
- 互信息计算公式如下:

代码实现:
from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(iris.data,iris.target)
SelectKBest(MIC, k=2).fit_transform(iris.data, iris.target)


互信息法一般用在特征x和标签y都是离散型的,求概率
4.2 嵌入法
Embedded:嵌入法,先使用某些机器学习的算法和模型进行训练,得到各个特征的权值系数,根据系数从大到小选择特征。类似于Filter方法,但是是通过训练来确定特征的优劣
4.2.1 基于树模型的嵌入法
树模型中可以输出feature_importances_属性,可以列出各个特征对树的建立的贡献,我们就可以基于这种贡献的评估,找出对模型建立最有用的特征
随机森林代码实现:
from sklearn.feature_selection import SelectFromModel#从模型里面进行选择
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier()#创建模型
SelectFromModel(clf,threshold=0.2).fit_transform(iris.data, iris.target)#阈值=0.2,表示选择特征重要性阈值>0.2的


4.2.2 基于惩罚项模型的嵌入法
- 用带有L1或L2正则化的项完成特征选择。正则化就是把额外的约束或者惩罚项加到已有模型(损失函数上,以防止过拟合并提高泛化能力
- L1正则化将系数w的l1范数作为惩罚项加到损失函数上,由于正则项非零,这就迫使那些弱的特征所对应的系数(coef)变成0。因此L1正则化往往会使学到的模型很稀疏(系数w经常为0),这个特性使得L1正则化成为一种很好的特征选择方法
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression
#带L1惩罚项的逻辑回归作为基模型的特征选择
#默认以10^(-5)作为阈值 也就是说求出来的系数如果小于这个阈值,那么就认为这个特征不重要
SelectFromModel(LogisticRegression()).fit_transform(iris.data, iris.target)

#惩罚项 C是正则化的系数
LR=LogisticRegression(penalty="l1", C=10,solver='liblinear')
LR.fit(iris.data, iris.target)
LR.coef_ #得到系数 重要的特征的系数会被求出来

4.3 包装法
Wrapper:包装法,根据目标函数(通常是预测效果评分),每次选择若干特征,或者排除若干特征
- 包装法在初始特征集上训练评估器,并且通过coef属性或通过feature_importances属性获得每个特征的重要性。然后,从当前的一组特征中修剪最不重要的特征。在修剪的集合上递归地重复该过程,直到最终到达所需数量的要选择的特征
- 包装法最常用的是递归特征消除(Recursive feature elimination,RFE),主要思想是反复的构建模型(如SVM或者回归模型)然后选出最好的(或者最差的)的特征,然后在剩余的特征上重复这个过程,直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序
递归特征消除法代码实现:
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression #逻辑回归模型
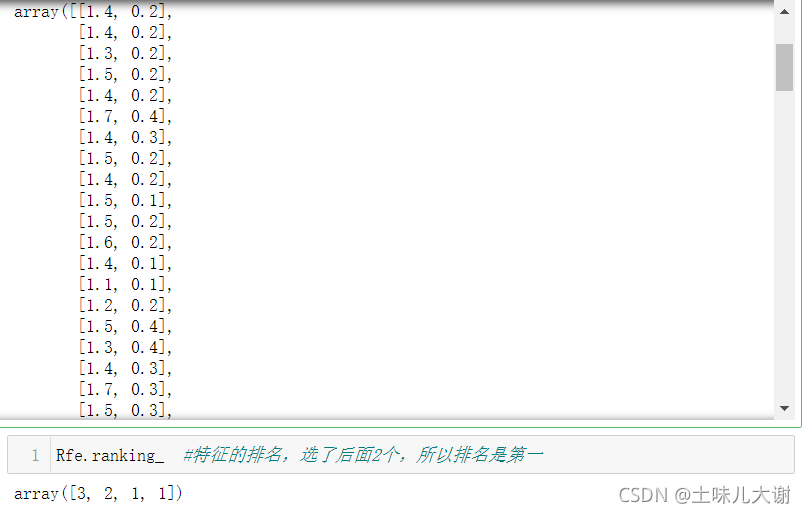
Rfe=RFE(estimator=LogisticRegression(), n_features_to_select=2)#n_features_to_select表示选择2个特征
Rfe.fit_transform(iris.data, iris.target)
#思想是:比如我们有4个特征,然后从4个特征里面先选3个特征进行组合比较,留下最好的;再从选出的这3个特征里面选2个特征组合进行比较,留下最好的

#C是惩罚项 C是正则化的系数;C越小,那么系数θ就越小;C的目的是为了约束系数θ,限制θ的大小
LR=LogisticRegression(penalty="l1", C=10,solver='liblinear')
LR.fit(iris.data, iris.target)
LR.coef_ #得到系数 重要的特征的系数会被求出来
五、特征转换
- 特征转换是指如何从已有的信息里面构造出新的有用的特征,这样可以用更少的特征来更好的描绘出来我们的模型,从而实现降维
- 特征转换和特征选择不同,特征选择是从我们已有的特征里面选择出来和目标值相关的特征,而特征转换是从已有的特征里面通过变换构造出来一些新的变量
- 常用实现方式:PCA(Principal Component Analysis),主成成分分析,其目的就是找到高维数据中的主成分,并利用 “ 主成分 ” 数据来表征原始数据,从而达到降维的目的
5.1 PCA(主成分分析)转换
信息的衡量
- 降维过程中,我们会减少特征的数量同时又保留大部分有效信息
- PCA使用的信息量衡量指标,就是样本方差,又称可解释性方差,方差越大,特征所带的信息量越多
主成分分析法的理解
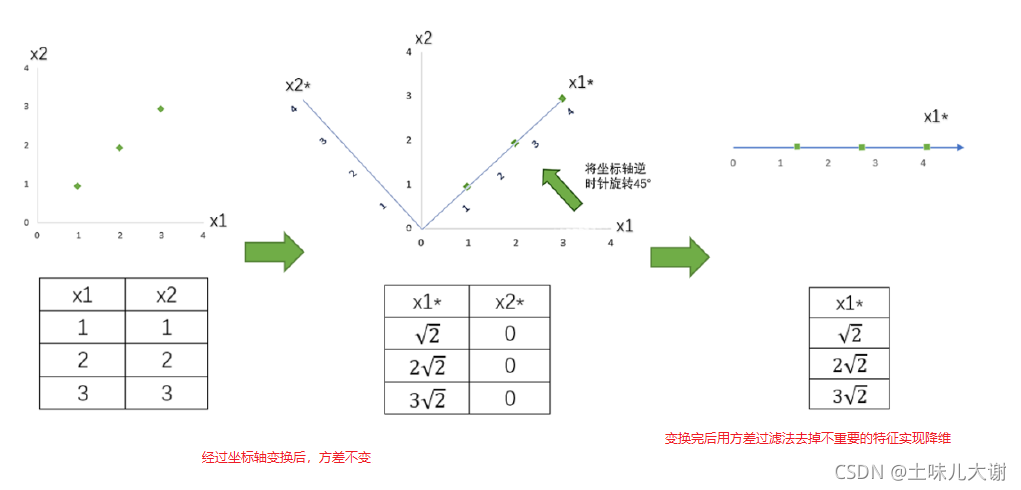
- 特征x1和x2,三个样本数据的坐标点分别为(1,1),(2,2),(3,3)
- 目标:只用一个特征向量来描述这组数据,即将二维数据降为一维数据,并且尽可能地保留信息量,即让数据的总方差尽量和原来一样
- 将原本的直角坐标系逆时针旋转45°,形成了新的特征向量x1和x2组成的新平面,在新的平面得到新的坐标
- 根据信息含量的排序,取信息含量最大的一个特征
代码实现:
还是以鸢尾花数据集为例
#PCA降维 主成分分析
from sklearn.decomposition import PCA
PCA(n_components=4).fit_transform(iris.data) #n_components表示降到4维
#先把数据中心化弄成零均值后,再对数据X乘以一个矩阵M(进行坐标轴变换)得到新的X
#PS:中心化只是减去了均值
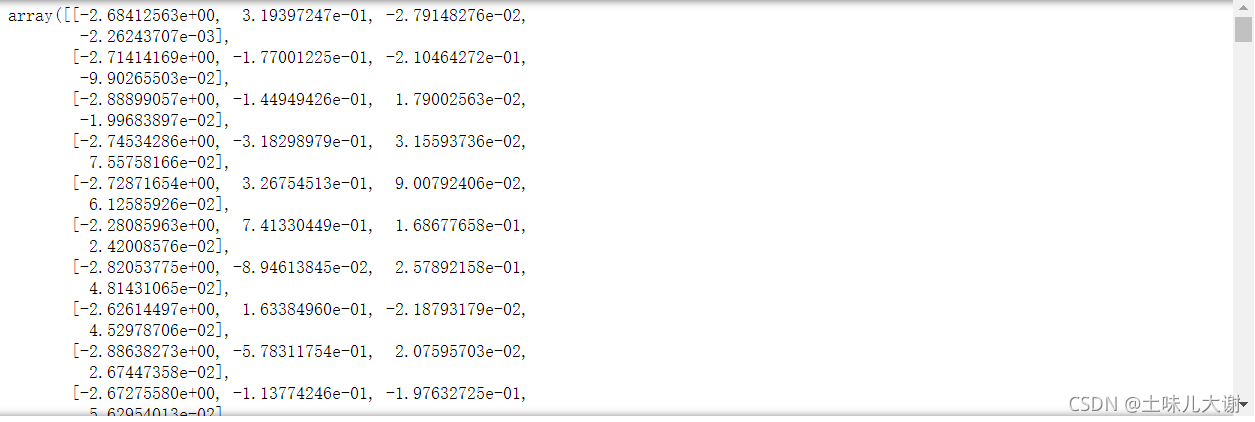
PCA(n_components=4).fit_transform(iris.data).var(axis=0) #查看改变后X的方差

PCA(n_components=2).fit_transform(iris.data) #表示降到2维;会把方差最小的两列删掉
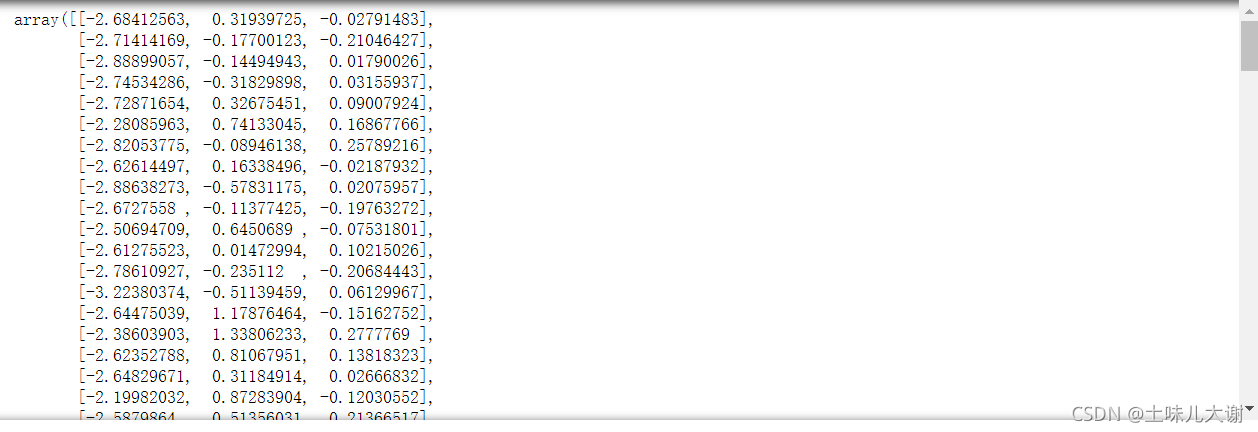
#某列或某几列方差/方差的和>0.9 若=0.9则降到一维
PCA(n_components=0.98).fit_transform(iris.data) #保留多少的信息量

from sklearn.decomposition import PCA
Pca=PCA(n_components=4)
Pca.fit_transform(iris.data) #表示降到4维
Pca.explained_variance_ #可解释方差
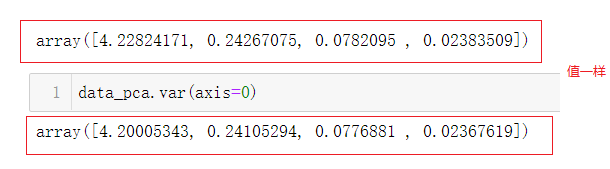
#cumsum()累积和
Per=Pca.explained_variance_.cumsum()/Pca.explained_variance_.sum()#累积和/总和
Per
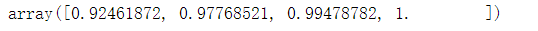
plt.plot(range(1,len(Per)+1),Per); #累计信息量曲线
#横轴是维度,纵轴是可解释方差
#特征的数量和总的可解释方差的曲线↓ 可以根据曲线决定要降到几维
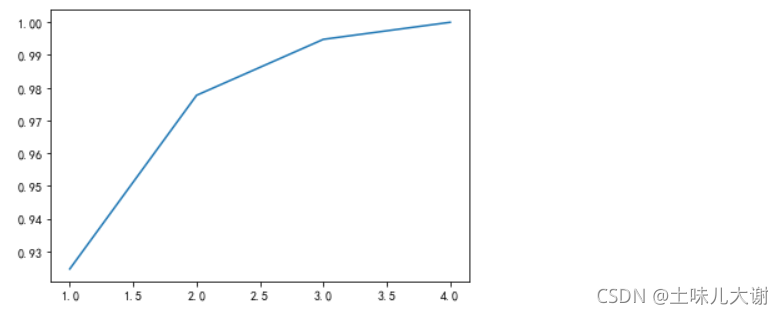
PS:进行降维的时候解释性会变差,性能也会变差一点
六、特征学习(用于深度学习的图像处理)
- 特征学习(feature learning),又叫表示学习(representation learning)或者表征学习,一般指模型自动从数据中抽取特征或者表示的方法,是模型自动学习的过程
- 传统的机器学习方法主要依赖人工特征处理与提取,而深度学习则依赖模型自身去学习数据的表示(自动抽取有效特征 )
特征难题
- 好的特征,特别在高维空间中的特征,很多情况下,是不容易直接由人类看出来的。那么,如何找到好的特征,就成为一个难题
深度学习中的特征学习
- 输入数据经过层层网络,依次被抽取出了低级特征比如边缘色度,中级特征比如纹理角点,和高级特征比如图形,然后把高度抽象化的高级特征交给最后的分类器层进行预测,从而得到分类结果
- 深度网络最后一层一般就是个线性分类器,比如softmax线性回归分类,深度神经网络的其他部分可以看做是为最后一层的分类器提供表征。通过层层网络抽取高度抽象化的特征,最终目的是为了帮助分类器做出好的预测:最开始输入网络的特征可能是线性不可分的,但是到最后隐藏层时变得线性可分了
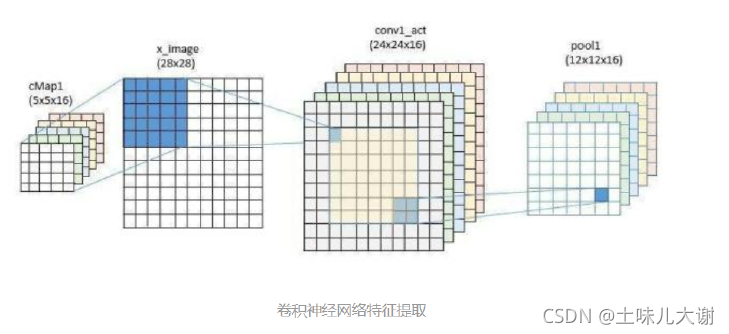
6.1 CNN中的特征学习
- 卷积(卷积就是一个特征提取的过程)神经网络,从字面上包括两个部分:卷积+神经网络。其中,卷积就是特征提取器,而神经网络,可以看作分类器。训练一个卷积神经网络,就是同时训练了特征提取器 (卷积) 和后面的分类器(神经网络)
- CNN是在多层神经网络的基础上,加入了“卷积层“进行特征学习,符合人脑对视觉任务的处理方式,并且其“局部感受野”和“权植共享”的概念,大大减少了网络参数的数量,解决了传统较深的网络参数太多难以训练的问题
特征的理解:

猫的识别:
-
大脑:通过眼睛,耳朵,嘴巴,尾巴,腿,或是这些的组合?这里的“耳朵,嘴巴,尾巴" 等等就是我们用来判断的"特征",大脑的神经元迅速完成了一系列复杂的运算,最后得出结论这是猫。“四条边,等长,直角”这些稍低级的特征可被大脑用来识别正方形
-
计算机:图片只是一堆数字而已,比如800x600的彩色图片就是一个800x600x3的矩阵,矩阵里相应元素的值就代表着像素值。那么什么样的数字代表“猫的眼睛”,什么样的数字代表“猫的耳朵”呢?如果采用特征工程,就需要理解数据并且人为定义规则来提取特征
CNN如何提取特征?
- 我们可以利用像素和邻域像素之间的差异,设计卷积核来提取图像的局部特征。经过不同卷积核的卷积运算后,可以起到不同的作用,比如高斯平滑卷积核可以被看做每个像素被其邻居像素平均(边缘模糊),而边缘检测的卷积核,就是将每个像素和其邻域像素做差值

卷积的理解
- 卷积运算其实就是向量的内积运算。内积是衡量两个向量之间的相似性的,所以卷积核在图像某一区域的卷积实际上就是这个卷积核与图像该区域的相似性
- 一个卷积核探索一种相似性,多个卷积核探索多个相似性
- 卷积核作用在同一样本的不同位置上(即卷积核在整张图上共享:权值共享)那么kernel探索的就是不同位置共有的局部特征,即局部特征的平移不变性。卷积核作用在不同的样本上,那么kernel 探索的是样本数据共有的局部特征
传统图像处理与深度学习的卷积核
- 传统的图像处理,是人工设计好不同的卷积核(滤波器)去提取不同特征,比如常见的滤波器:高通、低通、高斯模糊、SOBEL 查找边缘等,卷积核是白盒(即知道这个卷积核的作用,也知道里面具体的数据)。但缺点是非常依赖经验,提取规则只适用特定数据和问题,对于某些任务,特征并不单一和具体,很难设计适合的滤波器(很难找到合适的卷积核)。比如计算机视觉领域的目标检测:想要设计一个卷积核检测眼睛位置,但是不同的人,眼睛大小状态是不同的,如果卷积核太过具体化,卷积核代表一个睁开的眼睛特征,给出一张图片的眼睛是闭合的,就很大可能检测不出来。对于这种问题,我们如何设计卷积核呢,即如何确定卷积核的值呢?
- 深度学习可以自动寻找合适的卷积核来完成特征提取(卷积核的固定值被替换为参数来求解),得到的“滤波器”是黑盒,神经网络不需要理解数字代表的业务含义,它只需要尝试找到最合适的卷积核等各种参数,使得在给定数据上损失最小就可以了 (使得最终的卷积核,通过它提取出来的特征,能够使预测得到的结果和真值尽可能接近)
最终得到的特征
- 学习到的低级特征可视化后得到一些点,线,方向,颜色等等,中级特征可视化后可能是一些轮廓形状,角点等等,高级特征就更加抽象了甚至有时人类并不能理解