[人工智能]【论文学习】Transformer-XL

简介

RNN及其变体是训练语言模型（Language Modeling）的经典结构，其优点就是能够学习到序列之间的依赖关系，缺点：1）随着序列长度的增加，序列之间的依赖关系信息会逐渐丢失；2）单向；3）计算速度慢，只能step by step。截止到Transformer-XL，单向学习似乎是LM任务绕不过去的坎，XLNet使用PLM才比较隐蔽的解决单向学习语言模型的问题。

为了解决RNN存在的问题，Transformer-XL（XL表示extra long）沿用Transformer 中的“注意力机制”，但只是用Decoder部分学习语言模型。为了使用注意力机制学习语言模型， 1）继续沿用Mask Attention方法，使得预测当前词时，只能看到之前词的信息；2）引入“循环机制”、“相对位置编码”，提高了处理长文本的能力。第二点是本文的主要创新点。
?

模型

Vanilla Transformer

Transformer-XL引入的循环机制，参考了Vanilla Transformer的思想，因此先介绍下Vanilla Transformer模型。Vanilla对于长输入，在训练阶段，会将输入割裂成独立的几个部分（segment），然后分别处理。在推断阶段，每次取segment长度的输入进行处理，输出一个预测词，然后向右移动一个位置。如下图所示：

这样做有明显的缺点：1）编码或者推断过程，最多只能看到segment length的信息，当原始输入中存在长距离依赖关系时，会学习不足；2）割裂处理每一部分，产生了碎片化问题；3）在推断阶段，每次都从头计算，计算效率非常低。
?

recurrence mechanism

Transformer-XL中的循环机制的粒度是“segment”（后面称为切片），不像是RNN中以字为粒度的。另外一个显著不同点是，计算第$i+1$切片的第$N$层隐向量时，需要用到第 $i$ 个切片的第$N?1$层隐向量信息、以及第$i+1$切片的第$N?1$层隐向量。注意是“前一个切片的下一层的隐向量”，如下所示：

即对于第$i+1$切片的最后一层隐向量的最后一个位置，可以看到$N?L$范围的信息，$L$表示切片长度。 引入循环机制，使得信息可以在不同的segment之间流动，避免了碎片化。
?

相对位置编码

标准Transformer采用的是sin-cos相对位置编码（多头注意力机制是没有考虑输入序列的位置信息的，因此必须额外的引入位置信息，否则就类似词袋模型了），但由于没有引用“循环机制”，因此可以不采用相对位置的编码方式。而Transformer-XL由于引入了循环机制，因此必须考虑切片之间的相对位置信息，否则每一切片的同一位置信息是一致的，这显然不合理。假设某一切片内存在$i,j$两个位置，则这两个位置的：
$$\begin{gathered} a_{i,j}^{abs}=q_i^T?k_j=(W_q?(E(x_i)+U_i{)}^T?(W_k?(E(x_j)+U_j)) \\ =E_{x_i}^T?W_q^T?W_k?E_{x_j} \\ +E_{x_i}^T?W_q^T?W_k?U_j \\ +U_i^T?W_q^T?W_k?E_{x_j} \\ +U_i^T?W_q^T?W_k?U_j \end{gathered}$$

其中$U$表示PositionalEmbedding矩阵，该矩阵就是Transformer中使用的PE，是不需要学习的。论文对上面的四个子项进行优化，优化后如下

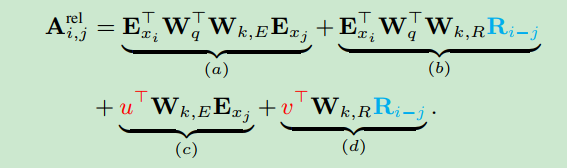
四项的含义可以参看原文，其中$u^T$、$v^T$、$W_{k,R}$是学习参数，$R$矩阵是PE矩阵，不需要学习。对上式重写：
$$A_{i,j}^{rel}=q_i^T{k}_j+q_i^T{W}_{k,R}{R}_{i?j}+u^T{k}_j+v^T{W}_{k,R}{R}_{i?j}$$

再将(a)、(c)项合并， (b)、(d)项合并，如下：
$$A_{i,j}^{rel}=(q_i^T+u^T)k_j+(q_i^T+v^T)W_{k,R}{R}_{i?j}$$

第一项中不涉及相对位置信息，直接进行矩阵计算就可以，第二项中由于包含$R_{i?j}$，因此需要进行相对位置转换。

对于$q_i^T{W}_{k,R}{R}_{i?j}$项，假设当前输入段的长度为$L$，缓存的Memory长度为$M$，则该项的shape为$L?(M+L)$， $R_{i?j}$取值范围为$[0,L+M?1]$。 当$R_{i?j}$逆序取值时:

令$Q_k^T=W_{k,R}{R}_{M+L?1?k}$， $Q$矩阵中的每一行表示一个相对位置：

$$Q=?\begin{array}{c}{R}_{M+L?1}^T\\ R_{M+L?2}^T\\ ...\\ R_0^T\end{array}?W_{k,R}^T$$
转换后

$$Q^T=?\begin{array}{c}{W}_{k,R}{R}_{M+L?1}\\ W_{k,R}{R}_{M+L?2}\\ ...\\ W_{k,R}{R}_0\end{array}?$$

则$$B=q{Q}^T=?\begin{array}{cccccc}{q}_0{Q}_0& ?& q_0{Q}_M& q_0{Q}_{M+1}& ?& q_0{Q}_{L+M?1}\\ q_1{Q}_0& ?& q_1{Q}_M& q_1{Q}_{M+1}& ?& q_1{Q}_{L+M?1}\\ ?& ?& ?& ?& ?& ?\\ q_{L?1}{Q}_0& ?& q_{L?1}{Q}_M& q_{L?1}{Q}_{M+1}& ?& q_{L?1}{Q}_{M+L?1}\end{array}?$$

显然B不是最终要求的(b)项，但存在很强的关联。对于第一行$q_0$，即$L$段的第一个元素，它与$L+M$中所有元素的相对位置关系为：“$M$、…、$1$、$0$… $L?1$”。 同理第二行的相对位置关系为“$M+1$、…、$2$、$1$… $L?2$”， 最后一个元素$q_{L?1}$的相对位置关系为“$M+L?1$、…、$L$、$L?1$… $0$”。即要求的(b)项为：
$$B_{shift}=?\begin{array}{cccccc}{q}_0{Q}_{L?1}& ?& q_0{Q}_{M+L?2}& q_0{Q}_{M+L?1}& ?& 0\\ q_1{Q}_{L?2}& ?& q_0{Q}_{M+L?3}& q_0{Q}_{M+L?2}& q_1{Q}_{M+L?1}& ?\\ ?& ?& ?& ?& ?& ?\\ q_{L?1}{Q}_0& ?& q_{L?1}{Q}_M& q_{L?1}{Q}_{M+1}& ?& q_{L?1}{Q}_{M+L?1}\end{array}?$$

注意当前单词只能看到之前出现的信息，不能看到之后的单词，因此有些位置最终的注意力得分为0。那么如何得到$B_{shift}$，只需对$B$进行如下转换：

    def _rel_shift(self, x, zero_triu=False):
        zero_pad = torch.zeros((x.size(0), 1, *x.size()[2:]),
                               device=x.device, dtype=x.dtype)
        x_padded = torch.cat([zero_pad, x], dim=1)

        x_padded = x_padded.view(x.size(1) + 1, x.size(0), *x.size()[2:])

        x = x_padded[1:].view_as(x)

        if zero_triu:
            ones = torch.ones((x.size(0), x.size(1)))
            x = x * torch.tril(ones, x.size(1) - x.size(0))[:,:,None,None]

        return x

这个技巧性很强，需要结合参考资料知乎上的图例加以理解。而对于D项，在实践上先和查询矩阵求和，在进行矩阵乘法、位置转换。 BD项计算完成之后，与AC项相加，得到最终的注意力得分。然后进行后面的加权求和等操作就可以预测下一个位置了。

?

参考资料

1. 论文 《Transformer-XL: Attentive Language ModelsBeyond a Fixed-Length Context》
2. Transformer-XL解读（论文 + PyTorch源码）https://blog.csdn.net/qq_22795223/article/details/106130388
3. 【核心代码解读】Transformer-XL https://zhuanlan.zhihu.com/p/74485142