[人工智能]xgboost算法

算法篇

xgboost算法

xgboost算法属于集成学习中的boosting类，又叫极端梯度提升树，是基于GBDT做的改进，但是基于的树模型都是回归树，因为回归树会计算出一个具体的值，这样才能比较真实结果和预测结果相差多少，在进行下一次的训练。

训练过程：一个模型一个模型串行训练
测试过程：一个样本输入，并行预测，预测结果相加，即可获得最终结果

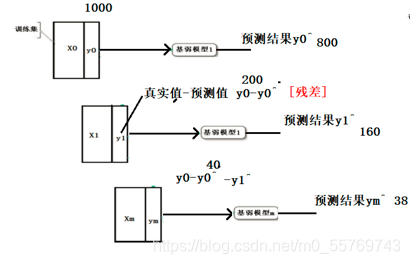
GBDT

首先来了解一下GBDT，GBDT叫做梯度提升树，是基于BDT（提升树）的改进，所谓提升树，就是后一棵树对前一棵树进行提升，就像集成学习中boosting类的原理，后一个学习器要在前一个学习器的基础上进行训练。

xgboost的目标函数

loss：损失函数，针对单个样本
cost：代价函数，针对整个数据集
obj：目标函数，代价函数+正则化
目标函数公式：

前面一项为：各个样本的损失函数的和，也就是代价函数
后面一项为：k棵树的复杂度累加和

xgboost的求解步骤

1. 由于boosting的预测结果是相加在一起的，所以前k棵树的预测结果等于前k-1棵树的预测结果加上第k棵树的预测结果，假设第0棵树的预测结果等于0，如下图
   
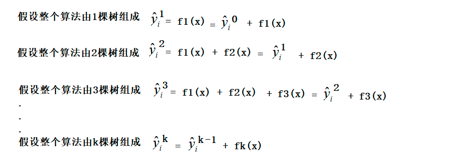
2. 将前k棵树的预测结果代入到目标函数中
   
3. 使用泰勒公式进行展开
   泰勒公式：
   
   
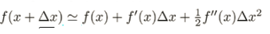
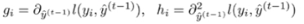
   通常用gi和hi来表示偏导的一阶导和二阶导，所以目标函数就变成了
   
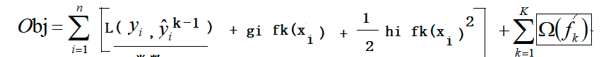
4. 由于我们计算的是k棵树的目标函数，所以前k-1棵树的损失函数就可以看成一个常数，而我们在方程中常数的表示方法通常是在最后加上一个C
   
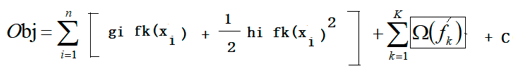
5. 到这前半部分已经处理完了，开始处理后半部分，也就是树的复杂度部分，计算树的复杂度的公式为
   其中T表示叶子结点个数，w表示每个叶子结点的取值，γ和λ是超参数，可暂时理解为学习率
   
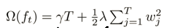
   所以我们可以将函数的后半段拆成前k-1棵树的复杂度加上第k棵树的复杂度
   
6. 同理可得，前k-1棵树的复杂度也是一个常数，可以放到函数最后，再将计算第k棵树的复杂度公式放进来，就变成了下面这样
   
7. 这时我们发现，前后累加和的参数不同，所以要想办法把它们统一。观察发现，前面的参数n是对样本的衡量，后面的T是对树的衡量。假如有这样一幅图
   
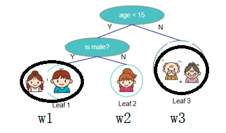
   总共有三个叶子结点，每个叶子结点对应的取值为w1、w2、w3，那么这五个样本对应的预测结果就分别是w1、w1、w2、w3、w3。将他们带入到公式中就是
   
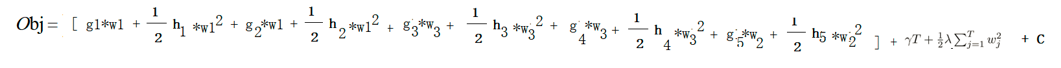
   将所有的g放在一起，将所有的h放在一起
   w1*(g1+g2), w2g5, w3(g3+g4)
   这里通常使用$I_j$累加对乘号后面的进行整合，也就是说会自动判断有一个叶子结点中有多少个样本，然后进行累加。通俗点理解就是$I_j$为某个叶子结点j上的样本集合。然后进行整合就会得到
   
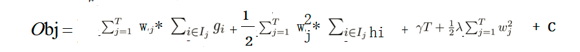
   这样就得到了统一累加的结果
8. 这里又会把某个叶子结点j上的样本的累加和表示为Gi，Hi
   
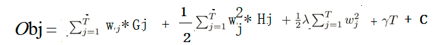
9. 把函数中所有的累加符号合并
   
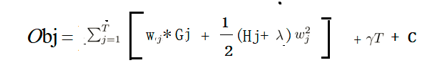
10. 对obj进行求导，化简
    
    
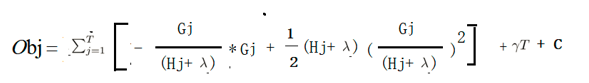
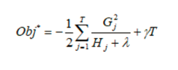
    得到最后结果，要求目标函数越小越好，也就是要求$\frac{G_j^2}{Hj+\lambda }$越大越好。

代码实现

# 安装 pip install xgboost
from xgboost import XGBClassifier  # 分类
from xgboost import XGBRegressor  # 回归
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from xgboost import plot_tree
from xgboost import to_graphviz  # 导出dot文件

from sklearn.datasets import load_iris

plt.rcParams["font.sans-serif"] = "SimHei"  # 设置支持中文字体
# matplotlib本身支持负号显示的。增加了支持中文显示，负号不能正常显示
plt.rcParams['axes.unicode_minus'] = False

x, y = load_iris(return_X_y=True)
out = load_iris()
f_name = out.feature_names
print("特征名称\n", f_name)

X_train, X_test, y_train, y_test = train_test_split(x,
                                                    y,
                                                    test_size=0.2,
                                                    stratify=y,
                                                    random_state=1
                                                    )

# 实例化
xgb = XGBClassifier(use_label_encoder=False,eval_metric='mlogloss')

xgb.fit(X_train, y_train)

acc = xgb.score(X_test, y_test)

print("准确率", acc)
print("训练集准确率", xgb.score(X_train, y_train))

# xgboost的自带的显示树不支持中文
# plot_tree(xgb, num_trees=0, fmap='iris2.fmap')  # 第1棵树
# plt.show()

# plt.scatter(x[:,-2], x[:,-1], c=y)
# plt.show()

# 如果要显示中文，先输出为dot文件
out = to_graphviz(xgb, fmap='iris2.fmap', num_trees=0)
out.render("iris.dot")