[人工智能]《DeepLearning.ai》第二课(1)：神经网络的编程基础

第二课(1)：神经网络的编程基础

2.1 二分类(binary classification)

遍历m个样本的训练集，神经网络通常不进行for循环遍历，神经网络计算中先进行前向传播，后进行反向传播。

逻辑回归是一个用于二分类的算法

例：加入图片大小为64*64像素，保存图片需要分别保存三个矩阵（红、绿、蓝三个颜色通道）

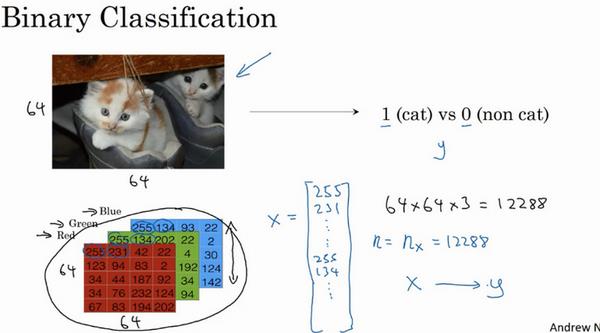
将所有颜色通道保存，得到$x$的总维度为$64?64?3$,因此$n_x=12288$?表示特征向量的纬度，如图所示，用小写$n$表示特征向量$x$?的纬度。因此问题转化为二分类中找到一个分类器输入图片的特征向量，预测输出结果$y=1/0$?,即预测图片中是否有猫。

符号定义:

对于一个单独的样本$(x,y)$,

$x$：表示一个$n_x$维数据，为输入数据，纬度为$(n_x,1)$;

$y$：表示输出结果，取值为$(0,1)$;

$(x^{(i)},y^{(i)})$：表示第$i$组数据，可能是训练数据，也可能是测试数据，此处默认为训练数据；例：$(x^{(1)},y^{(1)})$表示第一个样本的输入和输出，以此类推。?

$X=[x^{(1)},x^{(2)},...,x^{(m)}]$：表示所有的训练数据集的输入值，放在一个$n_x?m$的矩阵中，其中$m$表示样本数目，通常在python中用X.shape()来输出矩阵的纬度，即$n_x?m$?；

$Y=[y^{(1)},y^{(2)},...,y^{(m)}]$?：表示所有训练数据集的输出值，纬度为$1?m$??，Y.shape()。

$m$?：表示样本的个数，对于训练集$m_{train}$??,对于测试集$m_{test}$?

2.2 逻辑回归(Logistic Regression)

对一个算法进行预测通常是$y$?,也就是对实际值$y$?的估计，即$y$?表示$y=1$?的可能性或者是机会，前提是给定了输入特征$X$?。用$w$??来表示逻辑回归的参数，即特征权重?，维度与特征向量相同，b为表示偏差的实数（相当于机器学习课程中的偏置项$x_0=1,b={\theta }_0$?），$y=w^{T}x+b$?。该线性函数对于二分类问题来说并不是好算法。

希望$y$介于$0?1$之间，因此引入一个函数，即$sigmoid$?函数作用在输出上，如上图所示。

下图表示$sigmoid$函数：

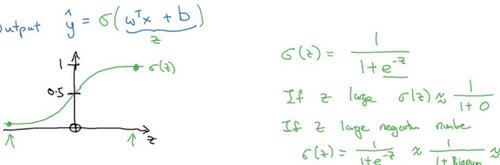
$sigmoid$函数公式如下：
$$\sigma (z)=\frac{1}{1+e^{?z}}$$
$z$是实数，$z$?无穷大时$e^{?z}$将会接近0，则$sigmoid$函数将接近1，相反$z$负无穷小，$sigmoid$?函数将接近0.

下一步要训练参数$w$和参数$b$?,因此需要定义一个代价函数。

2.3 逻辑回归的代价函数(Logistic Regression Cost Function)

为了训练参数$w$和$b$,需要定义代价函数，下面是逻辑回归的输出函数

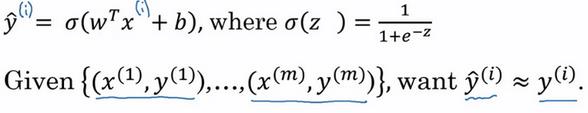
上标$(i)$表示数据的第$i$个训练样本。

逻辑回归中的损失函数：
$$L(y,y)=?ylog(y)?(1?y)log(1?y)$$
不使用预测值与实际值平方差的原因：采用这种方法找不到全局最优值。

需要保证损失函数尽可能小

当$y=1$时，损失函数$L=?log(y)$,要保证损失函数尽可能小，则$y$尽可能大。因为$sigmoid$函数取值为$[0,1]$,所以$y$会无限接近于$1$?。

当$y=0$时同样道理。

课程中很多情况类似，如果$y=1$,我们尽可能让$y$变大，如果$y=0$，我们尽可能让$y$?变小。

损失函数通常用来衡量单个训练样本的表现，当需要衡量全部训练样本的表现时，我们定义算法的代价函数，代价函数是对$m$个样本的损失函数求和然后除以$m$:
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L(y^{(i)},y^{(i)})=\frac{1}{m}\sum _{i=1}^m(?y^{(i)}log{y}^{(i)}?(1?y^{(i)})log(1?y^{(i)}))$$
因此，我们需要找到合适的$w$和$b$，使得代价函数$J$?的总代价降到最低。可以认为逻辑回归可以看做是一个非常小的神经网络。

2.4 梯度下降法(Gradient Descent)

在测试集上，通过最小化代价函数（成本函数）$J(w,b)$来训练参数$w$和$b$，

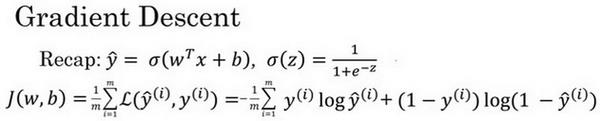
梯度下降形象化：

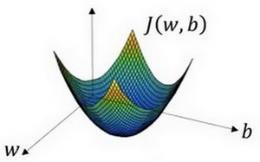
实际值$w$可以是更高纬度，如图代价函数是一个凸函数，像一个大碗一样，

$$w:=w?\alpha \frac{dJ(w,b)}{dw}$$

$$b:=b?a\frac{dJ(w,b)}{db}$$

梯度下降法：重复迭代如上两个公式

其中$\alpha$??为学习率(Learning rate)，用来控制步长，导数也就是斜率，这块没有找到那个希腊字母，用d代替求偏导数符号。

2.5 导数(Derivatives)

PASS

2.6 更多导数例子(More Derivative Examples)

PASS

2.7 计算图(Computation Graph)

2.8 使用计算图求导数

链式求导法则

程序中我们通常用$dvar$?来表示导数

2.9 逻辑回归中的梯度下降(Logistic Regression Gradient Descent)

单个样本的梯度下降算法更新：
$$w_1=?ad{w}_1,w_2=w_2?ad{w}_2,b=b?\alpha db$$

2.10 m个样本的梯度下降

损失函数的定义：
$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L(a^{(i)},y^{(i)})=\frac{1}{m}\sum _{i=1}^m(?y^{(i)}log{a}^{(i)}?(1?y^{(i)})log(1?a^{(i)}))$$

上面只进行了一步梯度下降，实际中需要重复该内容很多次。

缺点：需要两个for循环，第二个循环用来遍历所有特征，（通常for循环使得算法效率降低）

处理大量数据通常使用向量化的方法，下节课见