基于机器学习方法校准MPU6050陀螺仪加速度计(含源码)
最近组装了一架无人机,想要自己写一个飞控,所以一直在研究陀螺仪,我使用的是目前最常用的MPU6050六轴运动传感器,如下图所示

然而在将程序写好后发现传感器并不准确,会有数值漂移和误差,陀螺仪的数值漂移容易解决,直接加入偏置数置零即可,但是加速度计的误差却难消除,于是找到了一篇文章:一种适用于小型无人机的加速度计与陀螺仪的矫正方法,使用了文章中的线性校准,校准的模型如下

以上截图来自那篇文章,文章的做法为采集6个数据带入模型解得6个参数,但是我认为6个数据并不足够有代表性,应该采集尽可能多组数据进行非线性拟合,获得最优解,于是我采用了文章中的模型,基于机器学习的方法,以图中的S作为损失函数,采用梯度下降算法对kx,ky,kz,bx,by,bz进行训练,取得了非常好的效果,完整代码如下:
(本代码未使用AI框架,整个模型都是通过函数定义)
#采集77组加速度计x、y、z轴分量
x_acc = [6.2482,-9.0439,-8.6934,-7.4876,0.1998,3.1869,4.7792,-9.3825,-7.3979,-3.0565,-9.3239,2.4105,0.5575,1.0456,-7.0294,-7.5498,-6.18,-1.9368,9.7019,-10.1062,1.1724,4.1368,1.7873,4.4334,9.0571,8.7855,10.0751,8.2484,8.3142,6.6514,0.9211,-2.1414,-0.4008,-0.0383,1.8243,-2.4368,-1.4619,0.3637,0.1842,0.7154,0.2823,2.3854,1.0503,2.6378,1.7873,0.3302,0.1579,0.1543,-0.6472,0.055,0.2034,0.7405,0.1148,-0.1519,-1.1843,-0.908,-1.0635,-0.6699,-0.8733,-0.256,0.1017,9.9555,8.6851,9.934,10.7618,8.7604,8.6049,7.3261,5.5388,4.0435,-0.6962,-3.5602,-5.229,-7.1359,-8.1491,-9.4208,-9.6708]
y_acc = [0.3876,2.7802,0.0957,-1.1831,4.5494,-0.6867,-6.1525,1.3016,3.8808,0.8099,-0.914,-6.0365,7.1191,9.788,0.1794,5.7577,0.8111,-4.6045,1.0731,-1.6892,-5.4874,-2.3148,-0.8302,-0.6197,0.5658,-0.7884,0.579,1.0946,0.3708,1.1652,-0.0203,5.3725,9.6385,7.4457,-1.1173,0.5276,-7.2447,-9.7198,-8.0941,-4.7158,-5.0316,1.3422,-9.7749,-9.3358,-9.5213,-9.8179,-9.6505,-9.8,-8.9949,-9.3765,-10.0955,-9.4124,-7.1287,-4.388,-0.0275,2.8292,2.6546,8.1216,8.3334,9.6086,9.7988,-0.2524,3.3221,-0.4797,-2.4488,1.1078,0.8817,1.0396,-0.0646,-0.0634,-0.707,-0.8099,0.8123,0.3816,-0.0957,0.2285,-0.1651,]
z_acc = [-8.2329,-2.2119,-5.4359,-6.9983,-9.5954,-10.3323,-7.1191,-3.3532,-6.0664,-10.1756,1.3028,6.4324,5.875,-0.4953,-7.6299,0.9439,6.5102,7.4038,0.7896,0.0993,-8.8167,7.5498,8.8143,7.7831,4.8151,3.3317,-1.0575,-5.5891,-6.3499,-8.0606,-10.3347,-10.0129,-0.7238,5.2685,8.9303,9.0164,5.7829,-1.8219,-6.0353,-9.3825,-9.2377,-10.9891,-0.4031,0.2177,-0.0718,-0.4965,-0.5587,-0.6524,-4.4813,-1.6281,-0.2584,2.9572,6.0975,7.9422,8.8501,8.63,8.4147,4.8964,3.7707,1.6951,-1.5564,-0.9475,-3.9011,-1.8447,0.2991,2.8053,4.1033,5.4048,7.4541,8.2257,8.9195,8.258,7.2483,5.7386,4.1583,1.5827,-1.5947]
#初始化参数
k_x = 1
k_y = 1
k_z = 1
b_x = 0
b_y = 0
b_z = 0
#保存最好的参数值和损失函数值
sum_loss_min= 2108.283098842893
k_x_best = 0.9885173202329071
k_y_best = 0.9996695758960302
k_z_best = 0.9902671448306215
b_x_best = -0.1308841563162706
b_y_best = -0.01274923437960786
b_z_best = 0.8831292422279248
x_average = sum(x_acc) / len(x_acc)
y_average = sum(y_acc) / len(y_acc)
z_average = sum(z_acc) / len(z_acc)
print('x_acc:',len(x_acc),'y_acc:',len(y_acc),'z_acc:',len(z_acc))
print('x_aver:',x_average,'y_aver:',y_average,'z_aver:',z_average)
g = 9.80
delta = 1e-5
def LOSS(x,y,z,k_x_para,k_y_para,k_z_para,b_x_para,b_y_para,b_z_para):
loss = ( g**2 - (k_x_para * x+b_x_para)**2 - (k_y_para * y +b_y_para)**2 - (k_z_para*z+b_z_para)**2 ) **2
return loss
learning_rate = 1e-7
for epoch in range(1,10000+1):
"""
#动态调整学习率
if epoch>=4000:
learning_rate = 2e-6
elif epoch>=15000:
learning_rate = 1e-6
elif epoch>=20000:
learning_rate = 1e-7
"""
print("learning_rate:",learning_rate)
sum_loss = 0.00
sum_partial_derivative_k_x = 0.00
sum_partial_derivative_k_y = 0.00
sum_partial_derivative_k_z = 0.00
sum_partial_derivative_b_x = 0.00
sum_partial_derivative_b_y = 0.00
sum_partial_derivative_b_z = 0.00
for i in range(len(x_acc)):
#print('batch=',i)
loss = LOSS(x_acc[i] , y_acc[i] , z_acc[i],k_x,k_y,k_z,b_x,b_y,b_z)
partial_derivative_k_x = ( LOSS(x_acc[i] , y_acc[i] , z_acc[i] , k_x + delta, k_y, k_z, b_x, b_y, b_z) - loss ) / delta
partial_derivative_k_y = ( LOSS(x_acc[i] , y_acc[i] , z_acc[i] , k_x, k_y + delta, k_z, b_x, b_y, b_z) - loss ) / delta
partial_derivative_k_z = ( LOSS(x_acc[i] , y_acc[i] , z_acc[i] , k_x, k_y, k_z + delta, b_x, b_y, b_z) - loss ) / delta
partial_derivative_b_x = ( LOSS(x_acc[i] , y_acc[i] , z_acc[i] , k_x, k_y, k_z, b_x + delta, b_y, b_z) - loss ) / delta
partial_derivative_b_y = ( LOSS(x_acc[i] , y_acc[i] , z_acc[i] , k_x, k_y, k_z, b_x, b_y + delta, b_z) - loss ) / delta
partial_derivative_b_z = ( LOSS(x_acc[i] , y_acc[i] , z_acc[i] , k_x, k_y, k_z, b_x, b_y, b_z + delta) - loss ) / delta
sum_partial_derivative_k_x += partial_derivative_k_x
sum_partial_derivative_k_y += partial_derivative_k_y
sum_partial_derivative_k_z += partial_derivative_k_z
sum_partial_derivative_b_x += partial_derivative_b_x
sum_partial_derivative_b_y += partial_derivative_b_y
sum_partial_derivative_b_z += partial_derivative_b_z
sum_loss += loss
#print('epoch=',epoch,'batch=',i,'partial_derivative_k_x=',partial_derivative_k_x,'partial_derivative_k_y=',partial_derivative_k_y,'partial_derivative_k_z=',partial_derivative_k_z,'partial_derivative_b_x=',partial_derivative_b_x,'partial_derivative_b_y=',partial_derivative_b_y,'partial_derivative_b_z=',partial_derivative_b_z)
print('\n','epoch=',epoch-1,'sum_loss=',sum_loss,'\n')
print('epoch=',epoch,'learning_rate:',learning_rate)
print('epoch=',epoch,'kx偏导数=',sum_partial_derivative_k_x,'ky偏导数=',sum_partial_derivative_k_y,'kz偏导数=',sum_partial_derivative_k_z)
print('epoch=',epoch,'bx偏导数=',sum_partial_derivative_b_x,'by偏导数=',sum_partial_derivative_b_y,'bz偏导数=',sum_partial_derivative_b_z)
k_x = k_x - learning_rate * sum_partial_derivative_k_x
k_y = k_y - learning_rate * sum_partial_derivative_k_y
k_z = k_z - learning_rate * sum_partial_derivative_k_z
b_x = b_x - learning_rate * sum_partial_derivative_b_x
b_y = b_y - learning_rate * sum_partial_derivative_b_y
b_z = b_z - learning_rate * sum_partial_derivative_b_z
print('epoch=',epoch,'new:','k_x=',k_x,'k_y=',k_y,'k_z=',k_z)
print('epoch=',epoch,'new:','b_x=',b_x,'b_y=',b_y,'b_z=',b_z)
if sum_loss < sum_loss_min:
k_x_best = k_x
k_y_best = k_y
k_z_best = k_z
b_x_best = b_x
b_y_best = b_y
b_z_best = b_z
sum_loss_min = sum_loss
print('\n\n\n',k_x_best,'\n',k_y_best,'\n',k_z_best,'\n',b_x_best,'\n',b_y_best,'\n',b_z_best,'\n\n\n',sum_loss_min)
我将训练参数的初始值初始化为1,1,1,0,0,0,这种初始化是假设加速度计完全准确且无误差 ,在此基础上进行训练10000个epoch
训练效果如下图:
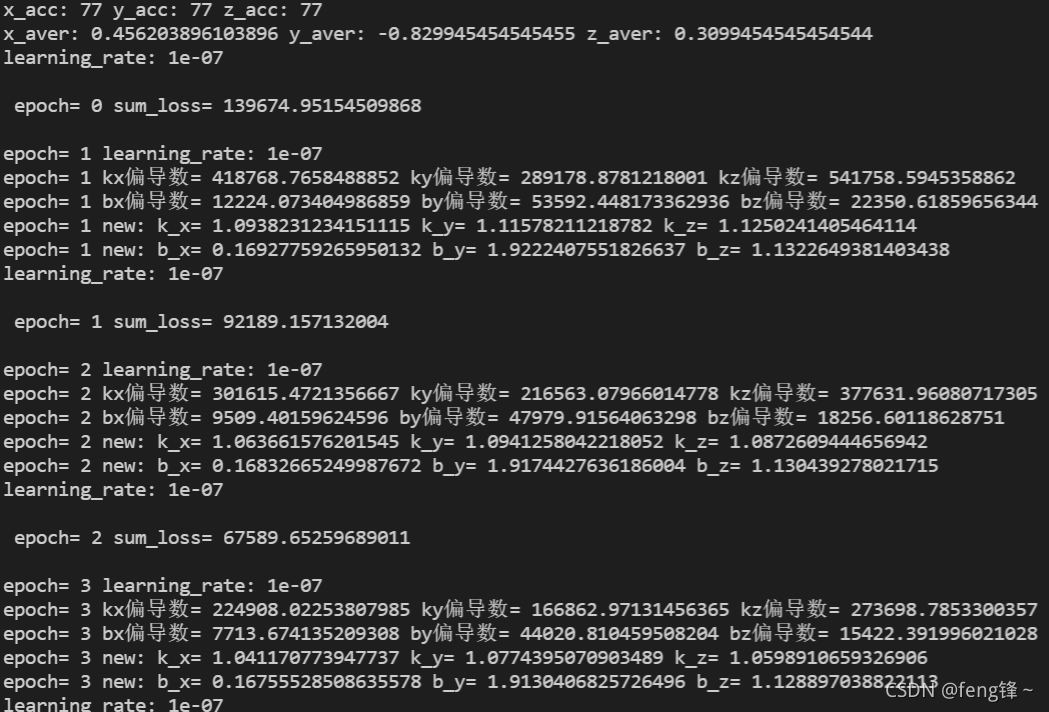
这是前3个epoch的训练效果图,可以看见,初始化值的sun_loss = 139674.95,这说明之前的假设不成立,加速度计存在误差
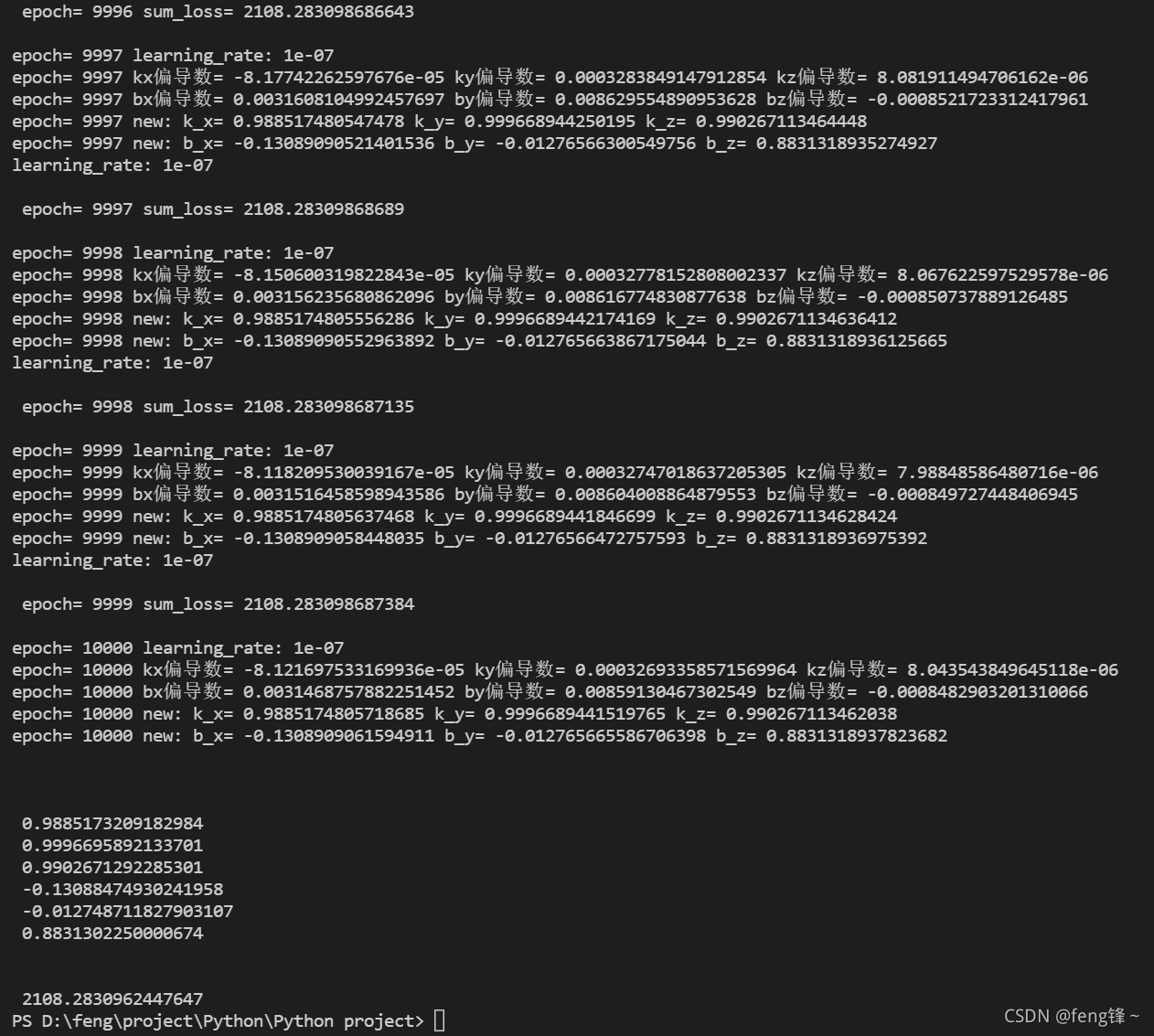
在训练完10000个epoch之后,sum_loss下降到2108,虽然看起来数值很大,但是考虑到这个误差是所采集的77组数据的误差的平方和的平方,实际每组数据的误差是非常非常小了,且sum_loss不再变化,说明已经收敛。
将训练得到的kx,ky,kz,bx,by,bz加入加速度计的程序中,发现校准的效果非常的好
第一张图是未校准之前,可以看出重力加速度az偏离g=9.80比较大,且ax,ay与理想值0有偏差,整体存在较大误差
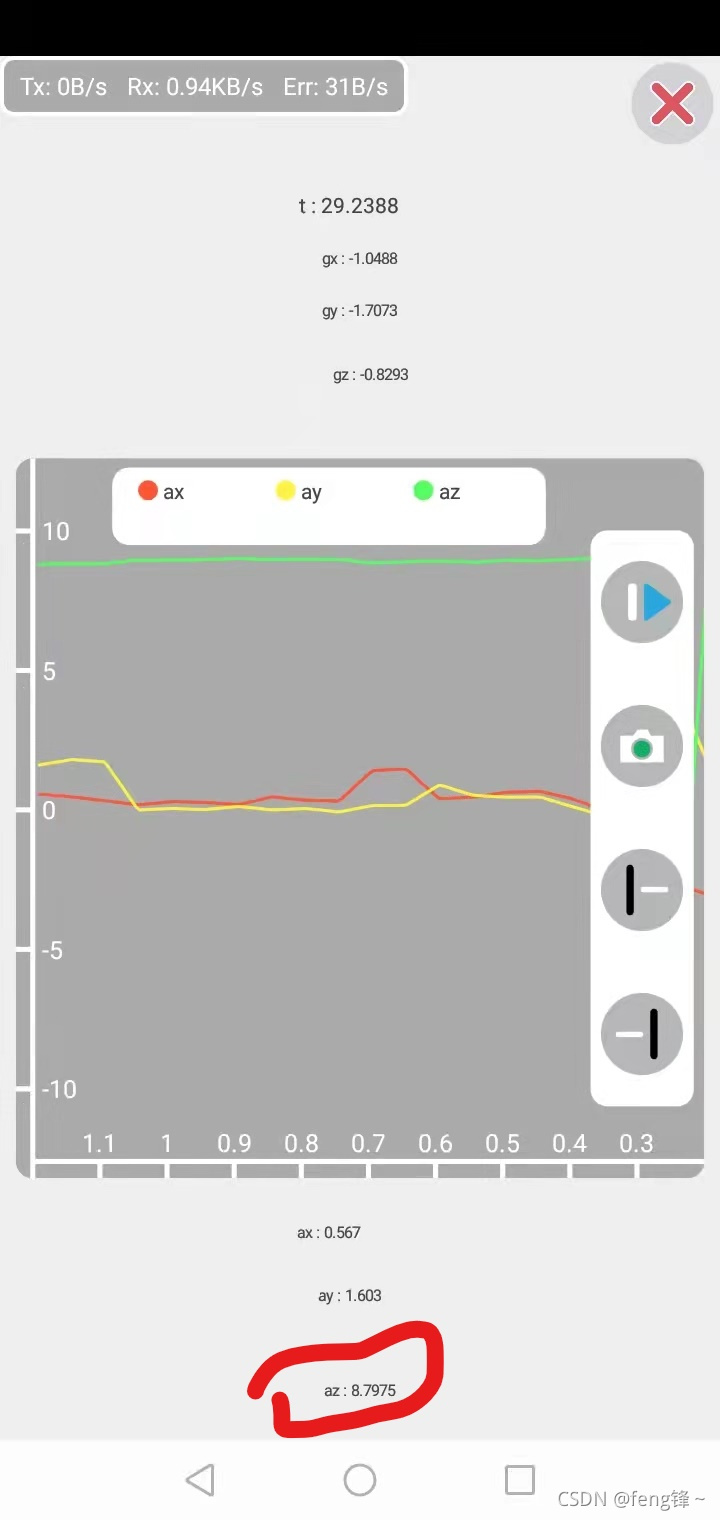
校准之后数据如下图,az数值非常接近重力加速度g=9.80,且ax,ay接近0,说明数据准确。
