[人工智能]利用XGBoost、Information Value、SHAP寻找“小北极星“指标与分层处理

前言

接着上一次的文章相关性研究思路及代码实现（MIC-最大信息系数、Relif-F特征选择算法、pearson、spearman、kendall、卡方检验、fisher精确检验、F检验、简单粗暴的分层聚合），之前谈到了如何通过计算三大相关性系数看各变量之间线性相关性强弱，以及卡方检验、fisher精确检验等计算特征分布的独立性，MIC、relief等计算信息含量。
这次做一个补充，其实很多情况下，上述这些方法足以找到些许相关性的线索，但之一的是，他们都是单一变量且粗颗粒度的结果，如果想让收益最大化，应当尽可能做到精细化地计算。

“小北极星”指标

所谓北极星指标，便是一个产品成功的关键指标。

曾几何时，人们关注所有者权益最大化的指标，或者简单讲就是净利润。所以为了增大净利润，我们所做的就是，增大主营业务收入同时扩充其他业务收入，同时降低边际成本、降低管理成本运营成本(增一切收入，降低一切成本)。我们可以看到，在”净利润“这个北极星指标的加持下，我们所做的一切行为都是最终导向它的。那么，这对一个企业真的就是好的嘛？

在这样的北极星指标的加持下，大部分公司会倾向于过分关注短期利益，而忽略长期发展。我们要想让企业长期发展，具有更强的创新力和竞争力，势必前期投入的成本会很大，甚至净利润是负的，这也就是为什么众多互联网公司直到现在估值上千亿，仍旧负利润的原因，但是这并不影响他们的估值，因为评估他们的价值的指标并不是简单的净利润，而是其他一些可以觉得公司未来发展和走向的指标，如：日活量、渗透率等。

好的北极星指标具备以下特点：

1. 它能够清楚表明产品在未来阶段需要优化的内容以及可被传达的功能点。
2. 它能够让公司内其他产品组的同事知道该产品组的实时进展，以便在需要时得到跨部门的资源协助。
3. 最重要的是，它使产品对结果负责。

北极星指标，可以通过拆解的方法一步步优化，如：转化率=转化人数/总触达人数，那么提升转化率的简单思路便是，转化的途径来源于哪些？如何提供这些途径的效率？如何减少低转化倾向的人群触达从而降低分母？如何最优的分配现有资源达到最优比率？诸如此类…

这是北极熊，不是北极星0.0…↑

好了，那么我们”小北极星"指标又是什么呢？假如今天的北极星指标就是转化率，那么什么影响转化率最显著？这个就是小北极星指标。 为什么分小北极星指标？因为现实中运营团队会分的很细，给小模块团队定指标，就要把大指标拆解成小指标，让每个团队甚至成员有更明确的业务目的。

传统的思路我们通过作图或者计算相关系数来进行单变量的分析，但在分析的变量or特征较多的时候，这样的方式效率极低，而且难易量化单变量对目标值的重要程度。因此，需要考虑因素机器学习特征工程的特征筛选和构造模型的一些过程，可以达到高效进行相关性、显著性分析的目的，从而决定小北极星指标。

下文中，我们将讲到，如何帮助团队找到显著性最强的小北极星指标，某种程度上讲，其实它更像是找相关性最强，影响程度最高的决定因素。此外，顺便总结下利用机器学习做分类和预测的简单方法。

Information Value(IV) 与 WOE

我们在使用决策树、逻辑回归等模型的时候，有很多特征假如300个，我们不可能把所有特征全部纳入模型中，这样首先会导致算力根本上内存过载耗时过大等因素，当然最重要的是…过多的特征会造成维度灾难。
因此我们需要提出很多”不重要“的特征，合并一些共线性的特征，也就是所谓的降维。

跑偏了…虽然上述是构建机器学习模型考虑的特征工程问题，但是在这一步，我们其实可以借鉴一下挑选”重要“特征的过程和方法。

挑选入模变量过程是个比较复杂的过程，需要考虑的因素很多，比如：变量的预测能力，变量之间的相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），变量在业务上的可解释性（被挑战时可以解释的通）等等。但是，其中最主要和最直接的衡量标准是变量的预测能力。

什么是IV？

IV的全称是Information Value，中文意思是信息价值，或者信息量。

从直观逻辑上大体可以这样理解“用IV去衡量变量预测能力”这件事情：我们假设在一个分类问题中，目标变量的类别有两类：Y1，Y2。对于一个待预测的个体A，要判断A属于Y1还是Y2，我们是需要一定的信息的，假设这个信息总量是I，而这些所需要的信息，就蕴含在所有的自变量C1，C2，C3，……，Cn中，那么，对于其中的一个变量Ci来说，其蕴含的信息越多，那么它对于判断A属于Y1还是Y2的贡献就越大，Ci的信息价值就越大，Ci的IV就越大，它就越应该进入到入模变量列表中。

简单讲，IV就是代表某个特征C多包涵能够预测目标Y的总信息量I的多少。

在计算IV之前，我们还要引用一个概念叫WOE，因为WOE的计算是IV计算的基础。

计算WOE的方法

WOE的全称是“Weight of Evidence”，即证据权重。WOE是对原始自变量的一种编码形式。

简单讲WOE就是这个特征各层级所占全部响应个体的权重，即是否它的改变能意味着目标响应群体的改变。

在计算WOE之前，我们首先要做的就是对数据进行离散化处理，也可以说是分箱、分组。

WOE计算公式如下：

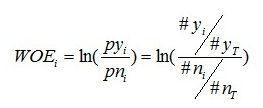
其中，

1. pyi是这个组中响应客户（指的是模型中预测变量取值为“是”或者说1的个体）占所有样本中所有响应客户的比例;
2. pni是这个组中未响应客户占样本中所有未响应客户的比例;
3. #yi是这个组中响应客户的数量;
4. #ni是这个组中未响应客户的数量;
5. #yT是样本中所有响应客户的数量;
6. #nT是样本中所有未响应客户的数量。

从公式中我们可以看出，WOE其实计算的就是分组当中这个变量"分组阳性的个体数占全部响应个体数的比例"与"分组阴性的个体数占所有未响应个体数比例"的比例差异之和。取对数是为了平滑处理。
变化一下得到如下公式：

其实也可以理解为该分组中阳性与阴性个体的比值/整体中阳性与阴性的比值。WOE越大，这种差异就越大，这个分组响应的可能性也就越大。WOE越小，差异就越小，这个分组样本响应的可能性也就越小。举个简单的例子，加入两个比值相等，那么就等同于：我整体的阳性阴性结果与你这个变量的加入没有半毛钱关系。

数据离散化

在计算WOE之前，我们首先要做的就是对数据进行离散化处理，也可以说是分箱、分组。我们这里只讲两种方法。

第一种方法非常简单，就是传统的按照四分位五分位数进行分箱，这样的方法的好处就是简单方便。但是呢，会存在一个问题，就是不同分组的数据间并不相互独立，这会影响最终的WOE计算结果，因此我们介绍下面这种方法。

第二种chi-merge算法，数据的相关性程度进行离散化。

chi-merge算法

chimerge是基于chi-squre的，监督的，自底向上（合并的）一种数据离散化方法。
这里我们首先需要了解卡方检验，具体参考相关性研究思路及代码实现（MIC-最大信息系数、Relif-F特征选择算法、pearson、spearman、kendall、卡方检验、fisher精确检验、F检验、简单粗暴的分层聚合） 上一次有详细介绍到手撸卡方检验的方法。

卡方检验

卡方检验是非参数检验，就是我们根本不知道分类变量的分布。
他比较适用于不是连续变量，而是两个二值型离散变量的情况，判断其是否相关。

计算思路
其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
四格卡方检验

我们可以看到，

• 实际值：爱吃炸鸡肥胖的频数占比为30.9%，不爱吃炸鸡肥胖频数占比为25%。
• 理论值：肥胖频数占比为28.3%

我们不能单纯从实际值看爱吃炸鸡是否对肥胖有影响，因为有可能存在抽样误差。
为了确定真实原因，我们先假设吃炸鸡对肥胖是没有影响的，即爱吃炸鸡和肥胖不是独立相关的，所以我们可以得出肥胖率理论值是（43+28）/（43+28+96+84）= 28.3%
基于这个假设理论比率，我们得到如下表格：

为了比较理论频数和实际频数的吻合程度或拟合优度，如果吃炸鸡和肥胖真的不是独立相关的，那么四格表里的理论值和实际值差别应该会很小。
卡方检验公式：
实际值与理论值的偏差方差大小与理论值之比。


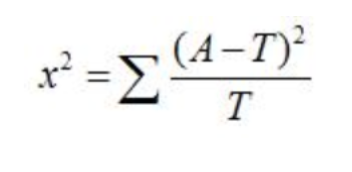
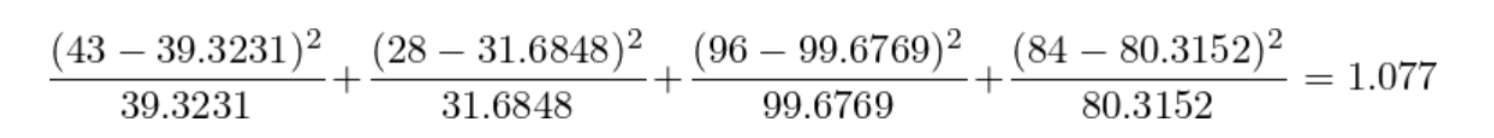
题外话，在自由度大于1、理论数皆大于5时，这种近似很好；当自由度为1时，尤其当1＜T＜5，而n＞40时，应用以下校正公式：

这个0.5叫做连续性修正，简单讲当理论值<5且>1，n>40(or30)的时候，分布类似于泊松分布，而卡方分布又是基于连续性的分布，需要做连续性修正。
连续性修成参考文献：

Confidence Intervals for a Proportion in Finite Population Sampling

建立假设检验：

• 原假设null hypothesis: 实际值与理论值是独立不相关的
• 备择假设alternative hypothesis: 实际值与理论值是独立相关的

我们查询一下chi-square临界表如下图：

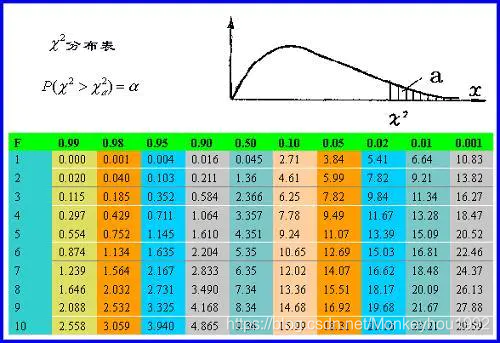
查询临界值就需要知道自由度。我们说，只要一种可能的话，自由度是0，有两种可能，自由度是1。如果抛不是一个硬币，而是一颗台球，上面数字只有一种可能，此时自由度是0。一个药片，吃下去的有三种结果：病治愈，病恶化，病不变，如果吃下去只有治愈这个可能，自由度是0，如果有三种可能，自由度是2。对于本例的表格而言，行和列的自由度都有自己的自由度，分别是行数和列数减一。又考虑到行数和列数的乘积是表中数值的总数，因此全表对应的自由度是行和列自由度的乘积。本例的自由度由此计算出来是1。

df (degree of freedom) = (col - 1)(row - 1) = (2-1)(2-1) = 1
查询可得，95%概率认为吃炸鸡与肥胖不相关的chi-square 是3.84， 因为1.077<3.84, 我们接受原假设，结论：吃炸鸡与肥胖无关！

chi-merge核心思想

某个属性的频率在相邻区间内应当相同，若其在相邻两个区间的分布独立，则这两个区间应当合并。

实现：

1. 将一个特征属性划分为多个区间；
2. 设置卡方阈值，例如三个类别的数据，在0.9的置信度夏，卡方值为4.6，即对于小于4.6的相邻区间相应合并。

代码实现：

1. chi-merge算法

import numpy as np


class ChiMerge:

    # def __init__(self, data, min_section_num):
    #     self.min_section_num = min_section_num
    #     self.dat = data
    def __init__(self, data_att, data_cla, max_section, length,col_name):
        self.dat = np.append(data_att, data_cla.reshape(length, 1), axis=1)

        self.max_section = max_section
        self.col = col_name


    # 计算初始信息熵
    @staticmethod
    def comp_init_entropy(cla_set):
        first_cla = 0
        second_cla = 0
        third_cla = 0
        for i in range(len(cla_set)):
            if cla_set[i] == 0:
                first_cla += 1
            if cla_set[i] == 1:
                second_cla += 1
            if cla_set[i] == 2:
                third_cla += 1

        n = len(cla_set)
        info = -first_cla / n * np.log2(first_cla / n) \
               - second_cla / n * np.log2(second_cla / n) \
               - third_cla / n * np.log2(third_cla / n)
        print(info)

    @staticmethod
    def merge_section(index_list, observe_list):

        """
        合并区间
        :param observe_list: 原来的区间集合
        :param index_list: 要合并的位置
        :return: 新的区间集合
        """
        # print(observe_list)
        number = int(len(index_list) / 2)
        for i in range(number):
            first_section = observe_list[index_list[2 * i]]  # 要合并的第一部分
            second_section = observe_list[index_list[2 * i + 1]]  # 要合并的第二部分
            new_section = []  # 合并后的区间

            min_value = float(first_section[0].split("~")[0])
            max_value = float(second_section[0].split("~")[1])
            first_class = first_section[1] + second_section[1]
            second_class = first_section[2] + second_section[2]
            third_class = first_section[3] + second_section[3]
            new_section.append(str(min_value) + "~" + str(max_value))
            new_section.append(first_class)
            new_section.append(second_class)
            new_section.append(third_class)
            # print(new_section)

            observe_list[index_list[2 * i]] = new_section
            observe_list[index_list[2 * i + 1]] = "no"
        for i in range(number):
            observe_list.remove("no")
        return observe_list

        # for i in  range

    @staticmethod
    def comp_chi(observe_list):
        """
        根据observe列表计算每个区间的卡方
        :param observe_list:排好的observe列表
        :return:最小chi所在的索引列表
        """
        min_chi = float('inf')  # 记录最小的chi
        # print(min_chi)
        index_list = []
        for i in range(int(len(observe_list) / 2)):
            chi = 0
            a1 = observe_list[2 * i][1]  # 第一个区间的信息
            b1 = observe_list[2 * i][2]
            c1 = observe_list[2 * i][3]
            d1 = observe_list[2 * i + 1][1]  # 第二个区间的信息
            e1 = observe_list[2 * i + 1][2]
            f1 = observe_list[2 * i + 1][3]
            n = a1 + b1 + c1 + d1 + e1 + f1
            a2 = (a1 + b1 + c1) * (a1 + d1) / n
            b2 = (a1 + b1 + c1) * (b1 + e1) / n
            c2 = (a1 + b1 + c1) * (c1 + f1) / n
            d2 = (a2 + b2 + c2) * (a1 + d1) / n
            e2 = (a2 + b2 + c2) * (b1 + e1) / n
            f2 = (a2 + b2 + c2) * (c1 + f1) / n
            if a2 != 0:
                chi += (a1 - a2) ** 2 / a2
            if b2 != 0:
                chi += (b1 - b2) ** 2 / b2
            if c2 != 0:
                chi += (c1 - c2) ** 2 / c2
            if d2 != 0:
                chi += (d1 - d2) ** 2 / d2
            if e2 != 0:
                chi += (e1 - e2) ** 2 / e2
            if f2 != 0:
                chi += (f1 - f2) ** 2 / f2
            if chi < min_chi:
                index_list.clear()
                index_list.append(2 * i)
                index_list.append(2 * i + 1)
                min_chi = chi
                continue
            if chi == min_chi:
                index_list.append(2 * i)
                index_list.append(2 * i + 1)
        # print(min_chi)
        # print(index_list)
        return index_list

    @staticmethod
    def init_observe(sort_data):  # sort_data为按属性排好的数据，格式为list套list
        """
        对observe列表进行初始化
        :param sort_data:
        :return:
        """
        observe_list = []
        for i in range(len(sort_data)):  # 每个sort_data[i]代表每个区间
            max_value = 0  # 存放每个区间的最大值和最小值
            min_value = 0
            section_name = str(sort_data[i][0]).split("~")
            if len(section_name) > 1:
                min_value = float(section_name[0])
                max_value = float(section_name[1])
            else:
                min_value = max_value = float(section_name[0])
            first_class = 0
            second_class = 0
            third_class = 0

            if min_value <= sort_data[i][0] <= max_value:
                if sort_data[i][1] == 0:
                    first_class += 1
                if sort_data[i][1] == 1:
                    second_class += 1
                if sort_data[i][1] == 2:
                    third_class += 1
            section_list = [str(min_value) + "~" + str(max_value), first_class, second_class, third_class]
            observe_list.append(section_list)
        # print(observe_list)
        return observe_list

    @staticmethod
    def comp_observe(sort_data):  # sort_data为按属性排好的数据，格式为list套list
        """
        计算observe列表（除了初始化之外）
        :param sort_data:
        :return:
        """
        observe_list = []
        for i in range(len(sort_data)):  # 每个sort_data[i]代表每个区间
            max_value = 0  # 存放每个区间的最大值和最小值
            min_value = 0
            section_name = str(sort_data[i][0]).split("~")
            if len(section_name) > 1:
                min_value = float(section_name[0])
                max_value = float(section_name[1])
            else:
                min_value = max_value = float(section_name[0])
            first_class = 0
            second_class = 0
            third_class = 0
            for j in range(len(sort_data)):
                if min_value <= sort_data[j][0] <= max_value:
                    if sort_data[j][1] == 0:
                        first_class += 1
                    if sort_data[j][1] == 1:
                        second_class += 1
                    if sort_data[j][1] == 2:
                        third_class += 1
            section_list = [str(min_value) + "~" + str(max_value), first_class, second_class, third_class]
            print(section_list)

    def chi_merge(self):  # dat为原始全部数据(包括类别)

        # min_section_num = 6  # 属性最终划分成几个区间
        for i in range(self.dat.shape[1] - 1):  # 对每个属性进行离散化
            now_section_num = self.dat.shape[0]  # 初始区间数为样本数量
            now_data = self.dat[:, [i, -1]]  # 当前要进行离散化的属性数据以及所属类别
            sort_data = now_data[now_data[:, 0].argsort()].tolist()  # 按当前属性从小到大排序，格式：[属性值，类别]
            # print(sort_data)
            observe_list = self.init_observe(sort_data)  # 得到初始化的observe列表
            while now_section_num > self.min_section_num:
                # print(observe_list)
                index_list = self.comp_chi(observe_list)
                observe_list = self.merge_section(index_list, observe_list)  # 更新区间集合
                # print(observe_list)
                now_section_num -= len(index_list) / 2
            print(observe_list)

    def comp_entropy(self, section_list):
        """

        :param section_list:
        :return: 当前划分的信息熵
        """
        sam_number = self.dat.shape[0]  # 总的样本数量
        final_entropy = 0
        for section in section_list:
            now_node_sam_number = section[1] + section[2] + section[3]
            now_node_entropy = 0
            if section[1] != 0:
                now_node_entropy += -(section[1] / now_node_sam_number) * (np.log2(section[1] / now_node_sam_number))
            if section[2] != 0:
                now_node_entropy += -(section[2] / now_node_sam_number) * (np.log2(section[2] / now_node_sam_number))
            if section[3] != 0:
                now_node_entropy += -(section[3] / now_node_sam_number) * (np.log2(section[3] / now_node_sam_number))

            # now_node_entropy = -(section[1] / now_node_sam_number) * (np.log2(section[1] / now_node_sam_number)) \
            #                    - (section[2] / now_node_sam_number) * (np.log2(section[2] / now_node_sam_number)) \
            #                    - (section[3] / now_node_sam_number) * (np.log2(section[3] / now_node_sam_number))
            final_entropy += (now_node_sam_number / sam_number) * now_node_entropy
        return final_entropy

    def find_best_merge(self):
        """
        寻找最合适的划分（根据信息熵）
        :return:
        """
        map_frame_ = pd.DataFrame(columns=['属性名称','范围'])
        for i in range(self.dat.shape[1] - 1):  # 对每个属性
            map_frame = pd.DataFrame(columns=['属性名称','范围'])

            print("第" + str(i + 1) + "个属性开始")
            # print(self.dat.shape[1] - 1)
            mini_entropy = float('inf')  # 存放某属性各种划分的最小熵
            best_section_info = []  # 存放最佳划分的区间数和区间信息
            for j in range(self.max_section):  # 划分的区间数为j
                # print(self.max_section)
#                 print("第" + str(i + 1) + "个属性" + "区间数为" + str(j + 1))
                now_section_num = self.dat.shape[0]  # 初始区间数为样本数量
                # print(now_section_num)
                now_data = self.dat[:, [i, -1]]  # 当前要进行离散化的属性数据以及所属类别
                # print(now_data)
                sort_data = now_data[now_data[:, 0].argsort()].tolist()  # 按当前属性从小到大排序，格式：[属性值，类别]
                observe_list = self.init_observe(sort_data)  # 得到初始化的observe列表
                k = 1
                while now_section_num > j + 1:
#                     print(now_section_num)
                    # print(j + 1)

#                     print("第" + str(i + 1) + "个属性" + "区间数为" + str(j + 1) + "第" + str(k) + "轮")
                    index_list = self.comp_chi(observe_list)  # 返回最小chi值的索引列表
                    observe_list = self.merge_section(index_list, observe_list)  # 更新区间集合
                    now_section_num -= len(index_list) / 2
                    k += 1
                # 此时划分区间数为j已完成，可以计算当前的信息熵
                # print(observe_list)
                now_section_entropy = self.comp_entropy(observe_list)

                if now_section_entropy < mini_entropy:
                    best_section_info.clear()
                    mini_entropy = now_section_entropy
                    best_section_info.append(j+1)
                    best_section_info.append(observe_list)
            print(best_section_info)
            alist = []
            for k in range(self.max_section):
                alist.append(best_section_info[1][k][0])
            map_frame['范围'] = alist
            map_frame['属性名称'] = self.col[i]
            map_frame_ = map_frame_.append(map_frame)
        map_frame_.reset_index(inplace=True,drop=True)
        return map_frame_
        
if __name__ == '__main__':
    col = list(test_continue_small.columns.values[0:-1])
    data_attr = np.array(test_continue_small[test_continue_small.columns.values[0:-1]])
    cla = np.array(test_continue_small['if_convert'])
    section_num = 5
    max_section_num = 5
    num_of_row=len(test_continue_small['if_convert'])
    chimerge = ChiMerge(data_attr, cla, max_section_num,length=num_of_row,col_name=col)  # 寻找区间数目小于max_section_num的划分
    map_frame_chimerge = chimerge.find_best_merge()

2. 简单分箱(分位数)

"""
quantile 分位分箱
"""

def map_frame(x,quant=None):
    alist = list(x.columns.values)
    final = pd.DataFrame(columns=['属性名称','范围'])
    for item in alist:
        aframe = pd.DataFrame(columns=['属性名称','范围'])
        temp = x[item]
        my_list = []
        for g in range(len(quant)-1):
            y1 = temp.quantile(quant[g])
            y2 = temp.quantile(quant[g+1])
            y = str(y1)+'~'+str(y2)
            my_list.append(y)
        aframe['范围'] = my_list
        aframe['属性名称'] = item
        final = final.append(aframe)
    final.reset_index(inplace=True, drop=True)
    return final
    
if __name__ == '__main__':
    map_frame = map_frame(test_continue[test_continue.columns.values[0:-1]],quant=[0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0])

计算WOE

数据离散化完成后，我们就可以开始根据上述公式计算WOE了，为了方便大家理解，举一个例子。

我们的目标是预测用户会不会买我们的商品(一只可爱的玩具🐒)，该监督值Y：1为会买，0为不会买。我们现在有历史数据500万条。有用户特征200个如：年龄、性别、学历、收入水平、城市…

那么，对于"收入水平”这一特征，我们计算它的WOE方法如下：

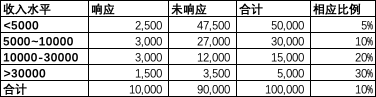
计算IV

我们从上述WOE的计算过程可以看出，其考虑了分组中响应与未响应比例距离总体响应/未响应比例的差异，但是并未考虑到，该分组是否占有较大的垂直成分比重。举个例子，如果某个分组的WOE计算结果非常大，但是这个分组只占总体数量的不到1%，那么我们能说这这个变量总体很显著嘛？不能。

所以IV是在WOE的计算基础上，加入垂直数量占比。

最后所有分组的IV加在一起，得到总的这个特征的IV值：

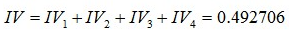
比较各特征IV值的大小，决定其该特征是否蕴含的信息足够大，足够显著。

代码实现：
附上我之前写的IV计算代码，不太适合数据量过大。(直接传参dataframe)

class Calc_IV_WOE:
    def __init__(self, data, map_list,max_section_num=None,attr_list=None,label_name=None,data_type=None):
        self.mp = map_list
        self.d = data 
        self.attr = attr_list
        self.label = label_name
        self.max_section_num = max_section_num
        self.type = data_type

    def calc_woe(self,z=None):
        temp = self.d[[self.attr[z],self.label]]
        temp['stas'] = 1
        X = temp[temp[self.label]==1]['stas'].sum()
        Y = temp[temp[self.label]==0]['stas'].sum()
        iv_list = []
        if self.type == 'continue':
            attr = self.attr[z]
            s = self.mp[self.mp['属性名称']==attr]
            s.reset_index(inplace=True,drop=True)
            for i in range(self.max_section_num):
                a = float(s.iloc[i]['范围'].split('~')[0])
                b = float(s.iloc[i]['范围'].split('~')[1])
                if z!=self.max_section_num-1:
                    if a!=b:
                        temp1 = temp[(temp[self.attr[z]]>=a)&(temp[self.attr[z]]<b)]
                    else:
                        temp1 = temp[(temp[self.attr[z]]==a)]
                else:
                    temp1 = temp[(temp[self.attr[z]]>=a)&(temp[self.attr[z]]<=b)]
                x = temp1[temp1[self.label]==1]['stas'].sum()
                y = temp1[temp1[self.label]==0]['stas'].sum()
                woe = math.log((x/y)/(X/Y))
                vertical = (x/X)-(y/Y)
                iv = vertical*woe
                iv_list.append(iv)
        elif self.type == 'discrete':
            attr = self.attr[z]
            s = self.mp[self.mp['属性名称']==attr]
            s.reset_index(inplace=True,drop=True)
            max_num = len(s.index.values)
            for i in range(max_num):
                a = float(s.iloc[i]['范围'].split('~')[0])
                b = float(s.iloc[i]['范围'].split('~')[1])
                if z!=self.max_section_num-1:
                    if a!=b:
                        temp1 = temp[(temp[self.attr[z]]>=a)&(temp[self.attr[z]]<b)]
                    else:
                        temp1 = temp[(temp[self.attr[z]]==a)]
                else:
                    temp1 = temp[(temp[self.attr[z]]>=a)&(temp[self.attr[z]]<=b)]
                x = temp1[temp1[self.label]==1]['stas'].sum()
                y = temp1[temp1[self.label]==0]['stas'].sum()
                woe = math.log((x/y)/(X/Y))
                vertical = (x/X)-(y/Y)
                iv = vertical*woe
                iv_list.append(iv)
        else:
            pass
        iv_ = sum(iv_list)
        return iv_

    def calc_iv(self):
        final = pd.DataFrame(columns=['属性名称','information_value_IV'])
#         temp = pd.DataFrame(columns=['属性名称','information_value(IV)'])
        raw1= []
        raw2 = []
        for i in range(len(self.attr)):
#             raw = pd.DataFrame(columns=['属性名称','information_value_IV'])
            iv = self.calc_woe(z=i)
#             print(iv)
#             raw['属性名称'] = self.attr[i]
#             raw['information_value_IV'] = iv
            raw1.append(self.attr[i])
            raw2.append(iv)
#             print(self.attr[i])
#             print(iv)
        final['属性名称'] = raw1
        final['information_value_IV'] = raw2
        final = final.sort_values(by='information_value_IV',ascending=False)
        final.reset_index(inplace=True,drop=True)
        return final
    
if __name__ == '__main__':
    calc = Calc_IV_WOE(test_continue, map_frame,max_section_num=10,attr_list=list(test_continue.columns.values[0:-1]),label_name='if_convert',data_type='continue')
    iv = calc.calc_iv()

IV的缺陷

从上述公式可以看出，如果该分组没有响应的数量，则IV就会倾向于无穷大，那么它便失去了意义。 因此遇到这种情况，我们需要重新分箱重做数据离散化的处理。

XGBoost算法-利用复杂的机器学习模型寻找显著性高的指标

特征重要性回答的问题是，哪些变量对模型的预测有最大的影响力。请注意这是在一个已经训练好的模型基础上。这里的重点是对预测能力的影响，而不是对组中目标变量Y的关系或者影响！！
如：你要是用random forest算法的时候，重要性是根据变量所在分裂点的深度计算，也就是参与构建树的次数。单颗decision tree的默认方法是gini importance,也就是变量分裂节点分别增加了多少纯度，或者说信息增益的累加值。

XGBoost是什么？

全称为eXtreme Gradient Boosting，是由我们华人骄傲陈天奇博士开发的，在GBDT的基础上对boosting算法进行的改进，内部决策树使用的是回归树。属于boosting迭代型、树类算法。适用范围为分类、回归。具有速度快、效果好、能处理大规模数据、支持多种语言、支持自定义损失函数等优点。

GBDT算法介绍

回归树的分裂结点对于平方损失函数，拟合的就是残差；对于一般损失函数（梯度下降），拟合的就是残差的近似值，分裂结点划分时枚举所有特征的值，选取划分点。最后预测的结果是每棵树的预测结果相加。

顺便简单看下bagging和boosting的区别

为集成学习的二个方法，其实bagging和boosting的实现比较容易理解，但是理论证明比较费力。所谓的集成学习，就是用多重或多个弱分类器结合为一个强分类器，从而达到提升分类方法效果。严格来说，集成学习并不算是一种分类器，而是一种分类器结合的方法。

bagging与boosting的区别

简要概述：

1. bagging就是每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中），共进行k轮抽取，得到k个训练集，k个模型。对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。
   典型算法代表：（并行）随机森林random forest
2. boosting是一族可将弱学习器提升为强学习器的算法。通过提高那些在前一轮被弱分类器分错样例的权值，减小前一轮分对样本的权值，而误分的样本在后续受到更多的关注。每一轮的训练集不变，只是训练集中每个样例在分类器中的权重发生变化.而权值是根据上一轮的分类结果进行调整。
   典型算法代表：（顺序进行）LightGBM、XGBoost

XGBoost基本原理

详见：XGBoost官方文档

1. 构造目标函数
我们最终的预测结果是k棵树预测结果之和，而目标函数的组成有两部分，第一部分是损失函数，表示真实值与预测值的差距，具体的损失函数可以选用MSE、交叉熵等；第二部分则是在控制树的复杂度，是一个惩罚项，经典的示例是正则化。树的复杂度可能会涉及到树的叶节点数、深度、叶节点值等。

2. 定义树的复杂度
树的复杂度包括：叶节点的个数、树的深度、叶节点值。定义好树的复杂度，就可以相对有效的控制过拟合以及泛化程度。


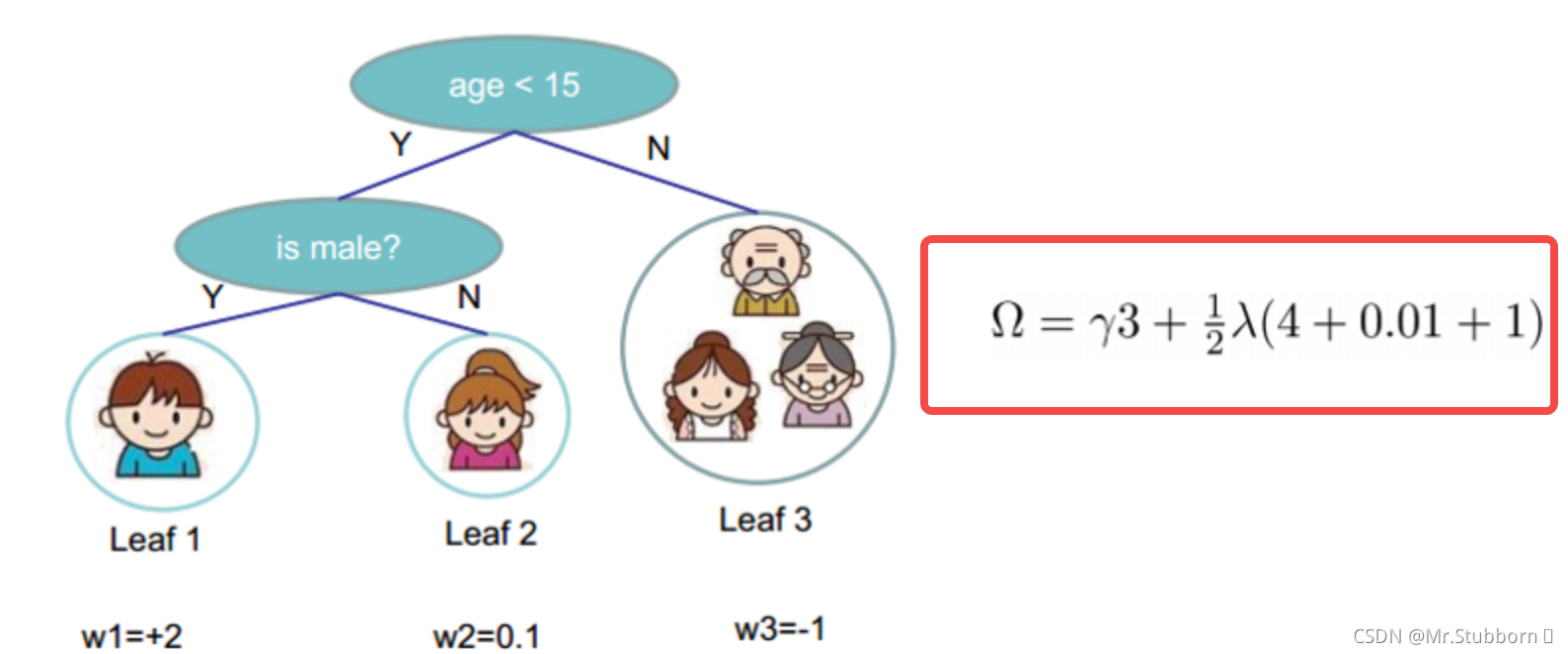
3. 集成树

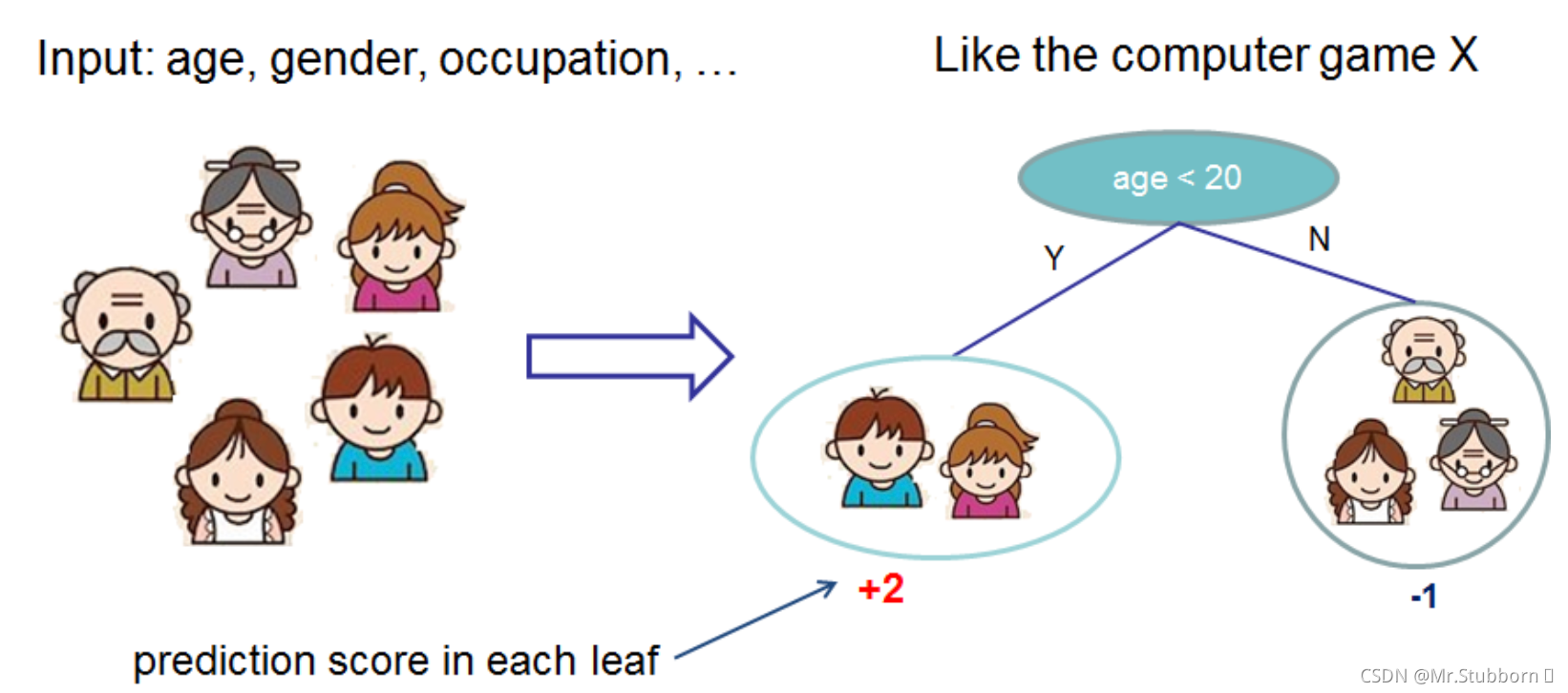
一棵树并没有很强的鲁棒性，因此我们同时会构建多棵树。

和传统的boosting tree模型一样，xgboost的提升模型也是采用的残差（或梯度负方向），不同的是分裂结点选取的时候不一定是最小平方损失。

4. Boosting

由上图我们可以看到，我们每一轮的训练和修正都是基于上一次的结果的优化，不断地优化我们的目标函数！

5. 对目标函数的改写

终的目标函数只依赖于每个数据点的在误差函数上的一阶导数和二阶导数。

6. 数结构的打分函数

Obj代表了当指定一个树的结构的时候，在目标上面最多减少多少structural score。我们选择每一次收益最大的那个branch，最终组成新的树结构。
这里有个感受，和rando forest不太一样的地方，随机森林是同时并行构造多棵树，准确率、精度的问题考虑在每一颗子树的构造上面，我们只选择泛化能力最强的那个。 但是对于xgboost，其实每一次迭代的过程，都是在选择误差最小的、受益最大的那棵树结构。

顺便简单看下回归树和分类树的区别

1. 分类树
穷举每一个feature的每一个阈值，找到使得按照feature<=阈值，和feature>阈值分成的两个分枝的熵最大的阈值(熵最大的概念可理解成尽可能每个分枝的男女比例都远离1:1)，按照该标准分枝得到两个新节点，用同样方法继续分枝直到所有人都被分入性别唯一的叶子节点，或达到预设的终止条件，若最终叶子节点中的性别不唯一，则以多数人的性别作为该叶子节点的性别。

总结：分类树使用信息增益或增益比率来划分节点（竟可能纯度更大）；每个节点样本的类别情况投票决定测试样本的类别。

2. 回归树
回归树的每个节点（不一定是叶子节点）都会得一个预测值，该预测值等于属于这个节点的所有数的平均值。分枝时穷举每一个feature的每个阈值找最好的分割点，但衡量最好的标准不再是最大熵，而是最小化均方差即(每个人的年龄-预测年龄)^2 的总和 / N。（也可以是其他损失函数）也就是被预测出错的人数越多，错的越离谱，均方差就越大，通过最小化均方差能够找到最可靠的分枝依据。

总结：回归树使用最大均方差（也可以是其他损失函数）划分节点；每个节点样本的均值作为测试样本的回归预测值。

代码实现：

"""
xgb-v2—删减版
"""
import matplotlib.pyplot as plt
import xgboost as xgb
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score


shanjian = res_[['a','b','c'.....]]
x_train, x_test, y_train, y_test = train_test_split(shanjian[shanjian.columns.values[1:-1]],
                                                   shanjian[shanjian.columns.values[-1]],
                                                   test_size=0.3,
                                                   random_state = 33)
xgb_model = XGBClassifier(learning_rate=0.1,
                         n_estimators=100,
                         max_depth=6,
                         min_child_weight=1,
                         gamma=0.,
                         colsample_btree=0.8,
                         objecttive='binary:logistics',
                         scale_pos_weight=1)
xgb_model.fit(x_train,
             y_train,
             eval_set=[(x_test,y_test)],
             eval_metric='auc',
             early_stopping_rounds=10,
             verbose=True)
fig, ax = plt.subplots(figsize=(10,10))

xgb.plot_importance(xgb_model.get_booster().get_score(importance_type='gain'),show_values=False,height=0.5,ax=ax,max_num_features=30)

我们可以得到如下模型特征重要水平：

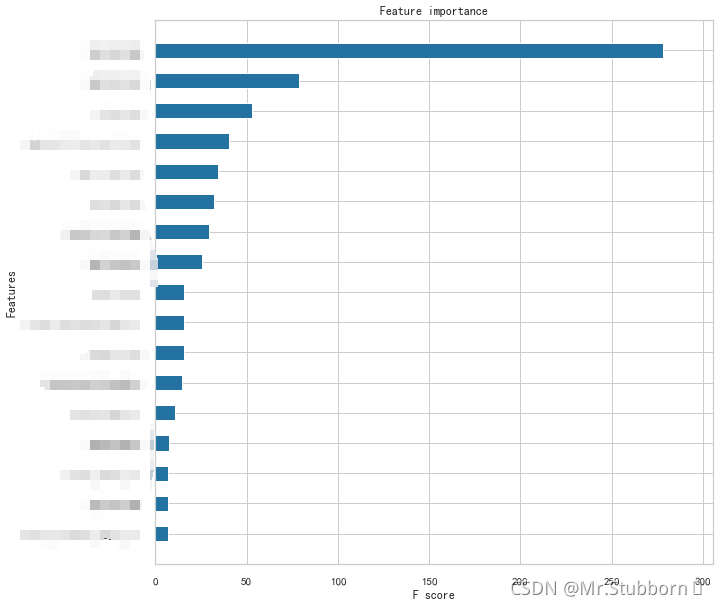
这个可以作为我们寻找小北极星指标的一个参考。

遇到缺失值怎么办？

XGBoost封装的包很强大，可以忽略缺失值直接替换。但如果是其他情况，我们需要自己写函数取替换。常见以下几种方法;

1. 简单粗暴的fillna(0)；
2. 简单粗暴的选择众数或者中位数去替换；
3. 用聚类的方法找到相似的族群用他们的中位数或者众数去替换。

具体的聚类算法操作，之前我有些过，可以参考聚类算法clustering 去选择合适的算法模型。

SHAP value解释XGBoost

Xgboost相对于线性模型在进行预测时往往有更好的精度，但是同时也失去了线性模型的可解释性。所以Xgboost通常被认为是黑箱模型。
在SHAP被广泛使用之前，我们通常用feature importance或者partial dependence plot来解释xgboost。 feature importance是用来衡量数据集中每个特征的重要性。其实就是每个特征对于提升这个模型的重要性，但是无法判断特征与最终预测结果的关系是如何的。

从上图中我们可以看到哪个特征对提升模型有很重要的影响，但是无法判断其正负的相关或者更复杂的相关性。于是这里引入SHAP。

参考：SHAP介绍

Shapley value起源于合作博弈论，SHAP是由Shapley value启发的可加性解释模型。对于每个预测样本，模型都产生一个预测值，SHAP value就是该样本中每个特征所分配到的数值。 假设第ii个样本为xixi，第ii个样本的第jj个特征为xi,jxi,j，模型对第ii个样本的预测值为yiyi，整个模型的基线（通常是所有样本的目标变量的均值）为ybaseybase，那么SHAP value服从以下等式：

yi=ybase+f(xi,1)+f(xi,2)+?+f(xi,k)yi=ybase+f(xi,1)+f(xi,2)+?+f(xi,k)

其中f(xi,1)f(xi,1)为xi,jxi,j的SHAP值。直观上看，f(xi,1)f(xi,1)就是对yiyi的贡献值，当f(xi,1)>0f(xi,1)>0，说明该特征提升了预测值，也正向作用；反之，说明该特征使得预测值降低，有反作用。

很明显可以看出，与上一节中feature importance相比，SHAP value最大的优势是SHAP能对于反映出每一个样本中的特征的影响力，而且还表现出影响的正负性。

代码实现：

"""
SHAP value
"""
import shap
explainer = shap.TreeExplainer(xgb_model)
shap_values = explainer.shap_values(res_[res_.columns.values[1:-1]])

global_shap_values_1 = pd.DataFrame(np.abs(shap_values).mean(0),index=x_train.columns).reset_index()
global_shap_values_1.columns = ['var','feature_importances_']
global_shap_values_1 = global_shap_values_1.sort_values('feature_importances_',ascending=False)
global_shap_values_1

shap.force_plot(explainer.expected_value, shap_values[0,:], res_[res_.columns.values[1:-1]].iloc[0,:])

shap.summary_plot(explainer.shap_values(res_[res_.columns.values[1:-1]]),res_[res_.columns.values[1:-1]])

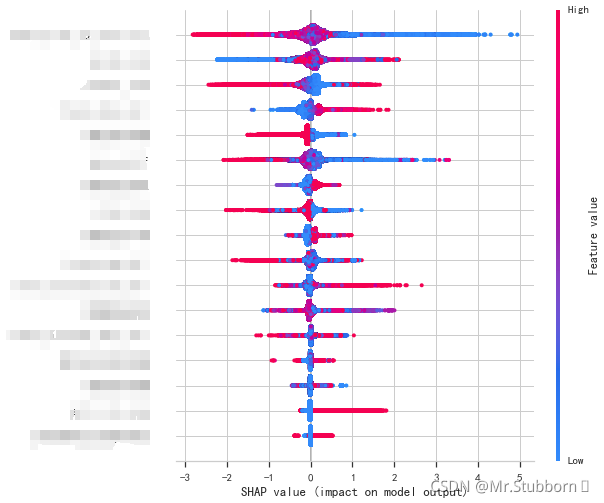
于是我们得到了如上非常fancy的一张图，我们现在看，颜色越红表明该特征队最终结果贡献越正向，越蓝则贡献越负向。