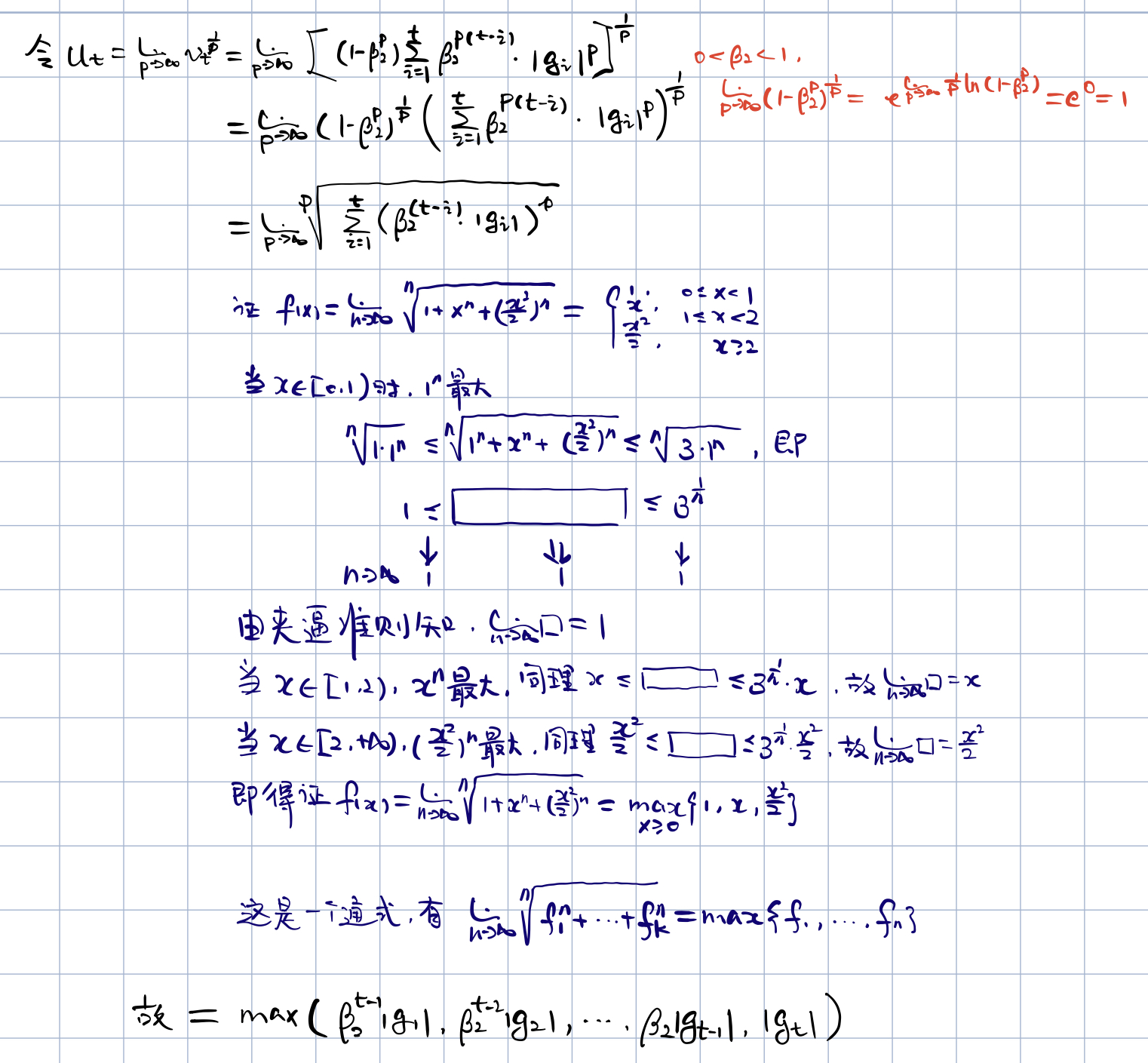[人工智能]【论文】Adam

【论文】Kingma D , Ba J . Adam: A Method for Stochastic Optimization[J]. Computer ence, 2014.（pdf）

论文首次提出了 Adam 算法——基于一阶导数的随机梯度下降算法

Adam 是对 SGD、AdaGrad 和 RMSProp 算法的优化

Adam 结合 AdaGrad 和 RMSProp 两种算法的优点，对梯度的一阶矩估计和二阶矩估计都进行综合考虑，具体算法如下

算法流程，

1. 计算 $t$ 时刻目标函数对 $\theta$ 的梯度
2. 计算梯度的一阶矩，即前面梯度与当前梯度的平均
3. 计算梯度的二阶矩，即前面梯度与当前梯度平方的平均
4. 对一阶矩 $m_t$ 进行校正，因为 $m_0$ 初始化为 $0$，会导致 $m_t$ 偏向于 $0$
5. 对二阶矩 $v_t$ 进行校正，因为 $v_0$ 初始化为 $0$，会导致 $v_t$ 偏向于 $0$
6. 更新参数 ${\theta }_t$，注意此时可将 $\frac{\alpha }{\sqrt{{\hat{v}}_t}+?}$ 视为更新参数 ${\theta }_t$ 的学习率，${\hat{m}}_t$ 视为更新参数 ${\theta }_t$ 的梯度

注意上述算法可以通过改变计算顺序而提高效率，将循环的最后三行替代为下面两条句

$$\begin{gathered} {\alpha }_t=\alpha ?\sqrt{1?{\beta }_2^t}/(1?{\beta }_1^t) \\ {\theta }_t\leftarrow {\theta }_{t?1}?{\alpha }_t?m_t/(\sqrt{v_t}+\widehat{?}) \end{gathered}$$

代码实现

# ADAM
# 以 y=x1+2*x2为例
import math
import numpy as np


def adam():
    # 训练集，每个样本有三个分量
    x = np.array([(1, 1), (1, 2), (2, 2), (3, 1), (1, 3), (2, 4), (2, 3), (3,
                                                                           3)])
    y = np.array([3, 5, 6, 5, 7, 10, 8, 9])

    # 初始化
    m, dim = x.shape
    theta = np.zeros(dim)  # 参数
    alpha = 0.01  # 学习率
    momentum = 0.1  # 冲量
    threshold = 0.0001  # 停止迭代的错误阈值
    iterations = 3000  # 迭代次数
    error = 0  # 初始错误为0

    b1 = 0.9  # 算法作者建议的默认值
    b2 = 0.999  # 算法作者建议的默认值
    e = 0.00000001  #算法作者建议的默认值
    mt = np.zeros(dim)
    vt = np.zeros(dim)

    for i in range(iterations):
        j = i % m
        error = 1 / (2 * m) * np.dot((np.dot(x, theta) - y).T,
                                     (np.dot(x, theta) - y))
        if abs(error) <= threshold:
            break

        gradient = x[j] * (np.dot(x[j], theta) - y[j])
        mt = b1 * mt + (1 - b1) * gradient
        vt = b2 * vt + (1 - b2) * (gradient**2)
        mtt = mt / (1 - (b1**(i + 1)))
        vtt = vt / (1 - (b2**(i + 1)))
        vtt_sqrt = np.array([math.sqrt(vtt[0]),
                             math.sqrt(vtt[1])])  # 因为只能对标量进行开方
        theta = theta - alpha * mtt / (vtt_sqrt + e)

    print('迭代次数：%d' % (i + 1), 'theta：', theta, 'error：%f' % error)


if __name__ == '__main__':
    adam()

$m_t$ 和 $v_t$ 的偏差修正

可以将 $v_t={\beta }_2?v_{t?1}+(1?{\beta }_2)?g_t^2$ 改写为所有时间步上只包含梯度和衰减率的函数，即 $$v_t=(1?{\beta }_2)\sum _{i=1}^t{\beta }_2^{t?i}?g_i^2$$

下面我们用数学归纳法简单证明一下

我们知道梯度的真实一阶矩为 $E(g_t)$，真实的二阶矩为 $E(g_t^2)$。现在，我们希望知道的是时间步 $t$ 上指数移动均值的期望 $E(v_t)$ 与真实的二阶矩 $E(g_t^2)$ 之间的差异，这样才好对这两个量之间的偏差进行修正

我们可以简单通过下面代码模拟看一下初始值的影响

import numpy as np
import matplotlib.pyplot as plt

beta = 0.9
num_samples = 100

np.random.seed(0)
raw_data =  np.random.randint(32, 38, size = num_samples)
x_index = np.arange(num_samples)

v_ema = []
v_pre = 0
for i, t in enumerate(raw_data):
    v_t = beta * v_pre + (1 - beta) * t
    v_ema.append(v_t)
    v_pre = v_t

    v_ema_corr = []
    for i, t in enumerate(v_ema):
        v_ema_corr.append(t / (1 - np.power(beta, i + 1)))

plt.plot(x_index, raw_data, label='raw_data')  # Plot some data on the (implicit) axes.
plt.plot(x_index, v_ema, label='v_ema')  # etc.
plt.plot(x_index, v_ema_corr, label='v_ema_corr')
plt.xlabel('time')
plt.ylabel('T')
plt.title("exponential moving average")
plt.legend()
plt.savefig('./ema.png')
plt.show()

可以看到不经过修正的指数移动平均值在初始阶段阶段的结果与真实的曲线有很大的偏差，但是这种偏差随着步数的增加会越来越小；当然，经过修正的指数移动平均值在开始就可以很好的跟踪真实变化趋势

一阶矩、二阶矩

由前面可知，一阶矩 $E(g_t)$ 即当前梯度 $g_t$ 的期望（估计一阶矩 $m_t$），由于当前梯度 $g_t$ 是随机采样得到的估计结果，因此更关注它在统计意义上的期望

二阶矩 $E(g_t^2)$ 即当前梯度的平方 $g_t^2$ 的期望（估计二阶矩），考虑它的意义要分四种情况：

• 当 $v_t$ 很大且 $||m_t||$ 很大时，说明梯度大且稳定。$v_t$ 是梯度平方的指数移动均值自然结果为正，当 $v_t$ 很大，说明过往大部分的梯度与当前梯度的绝对值都不会太小。$||m_t||$ 指的是当前梯度指数移动均值的绝对值，当 $||m_t||$ 很大，则说明过往梯度与当前梯度正负抵消的很少，即过往梯度与当前梯度一般是同号。这样，梯度更新相对稳定，过度平滑，可以看成梯度下降在**『走大下坡』**，梯度下降方向明确
• 当 $v_t$ 很大而 $||m_t||$ 却很小时，则说明过往的大部分梯度和当前梯度的绝对值都很大，但是出现了很多的正负抵消的情况。此时，梯度更新**『处于震荡的状态』**，一会儿正，一会儿负，但由于 $g_t^2$ 的指数移动均值很大，说明单个梯度的绝对值很大，可能是向下更新到一个局部的波谷，有进行一波反弹
• 当 $||m_t||$ 但是 $v_t$ 却趋于零，这种情况不可能会出现
• 当 $||m_t||$ 趋于零且 $v_t$ 也趋于零时，『可能达到局部最低点，也可能走到一个极度平缓的地方』，此次要避免陷入平原

梯度更新

Adam 更新规则的一个重要特性时其步长的谨慎选择。假设 $?=0$，时间步 $t$ 下参数空间中的有效步长是 ${\Delta }_t=\alpha ?{\hat{m}}_t/\sqrt{{\hat{v}}_t}$

这个有效步长有两个明确的上界：

1. 在 $(1?{\beta }_1)>\sqrt{1?{\beta }_2}$ 的情况下，有效步长的上确界满足 $|{\Delta }_t|?\alpha ?(1?{\beta }_1)/\sqrt{1?{\beta }_2}$
2. 在其他情况下 $|{\Delta }_t|<\alpha$

第一种情况只有在极稀疏的情况下才会发生：即梯度除了当前时间步不为 0，其余时间步上梯度都为 0；而在不那么稀疏的情况下，有效步长会变得更小

当 $(1?{\beta }_1)=\sqrt{1?{\beta }_2}$ 时，我们有 $|{\hat{m}}_t/{\hat{v}}_t|<1$，此时我们可以确定出上确界 $|\Delta |<\alpha$

在更通用的场景中，因为 $|E(g)/\sqrt{g^2}|?1$，我们有 ${\hat{m}}_t/\sqrt{{\hat{v}}_t}\approx \pm 1$，于是每一个时间步的有效步长在参数空间中的量级近似受限于步长因子 $\alpha$， 即 $|{\Delta }_t|<\alpha or|{\Delta }_t|\approx \alpha$。这可以理解为在当前参数值下确定了一个置信域区间，这个置信域区间提供了一些当前梯度估计没有提供的信息。于是，通过其通常便可以提前知道正确的 $\alpha$ 取值的右边界

对于多数机器学习模型来说，我们知道好的最优状态是在参数空间内的集合域上有着极高的概率，例如，我们可以在参数上有一个先验分布。$\alpha$ 确定了参数空间内有效步长的上确界，通常也就可以推断出 $\alpha$ 的正确量级，而最优解也可以从 ${\theta }_0$ 开始通过一定数量的跌倒到达这个正确的量级

我们将 ${\hat{m}}_t/{\hat{v}}_t$ 称作信噪比（SNR），如果 SNR 值较小，那么有效步长 ${\Delta }_t$ 将接近于 0，目标函数也将收敛到极值。这是十分令人满意的，因为越小的 SNR 意味着就判断 ${\hat{m}}_t$ 的方向是否符合真实梯度方向这点上有着越大的不确定性。例如，SNR 值在最优解附近通常会趋近于 0，这同时也导致了在参数空间中使用更小的有效步长，这类似于一种自动退火的机制

对于不同的梯度范围来说，有效步长 ${\Delta }_t$ 是不变的，如果将梯度 $g$ 乘以一个系数 $c$ 进行缩放，那么 ${\hat{m}}_t$ 也要乘以一个一样的系数因子 $c$，而 ${\hat{v}}_t$ 则乘以系数 $c^2$，而最终的结果并不产生变化 $(c?{\hat{m}}_t)/(\sqrt{c^2?{\hat{v}}_t})={\hat{m}}_t/\sqrt{{\hat{v}}_t}$

Adam 算法的优点

• 惯性保持
  Adam 记录了梯度的一阶矩，即过往梯度与当前梯度的指数移动平均值，是的每一次更新时，上一次更新的梯度与当前更新的梯度不会相差太大，即梯度平滑、稳定的过度，可以适应不稳定的目标函数
• 环境感知：
  Adam 记录了梯度的二阶矩，即过往梯度批平方与当前梯度平方的平均，为不同参数产生自适应的学习速率
• 超参数易控制
  $\alpha 、{\beta }_1、{\beta }_2、?$ 具有良好的解释性，且通常无需调整参数或仅需很少的调整

AdaMax

前面我们有 $$v_t=(1?{\beta }_2)\sum _{i=1}^t{\beta }_2^{t?i}?g_i^2$$，这可以看成一个关于 $g_i$ 的 $L^2$ 范数，换句话说，权重 ${\theta }_t$ 的各维度上的增量是根据该维度上当前和过往梯度的 $L^2$ 范数。我们可以从 $L^2$ 范式的更新规则推广到 $L^p$ 范数的更新规则，但是 $p$ 值越大，推广算法在数值上将变得不稳定。在特例中，作者让 $p\to \infty$ 可以的得到一个极其稳定且简单的算法

在 $L^p$ 范数的情况下，$$v_t=(1?{\beta }_2^p)\sum _{i=1}^t{\beta }_2^{p(t?i)}?|g_i{|}^p$$

于是，我们就得到了算法 2 里面的公式 $u_t=max({\beta }_2?u_{t?1},|g_t|)$，初始化时 $u_0=0$

在算法 2 里面我们不需要对初始化偏差作出修正。同时，参数更新的范围也有一个更加简洁的界限：$|{\Delta }_t|?\alpha$