[人工智能]CNN卷积神经网络学习笔记

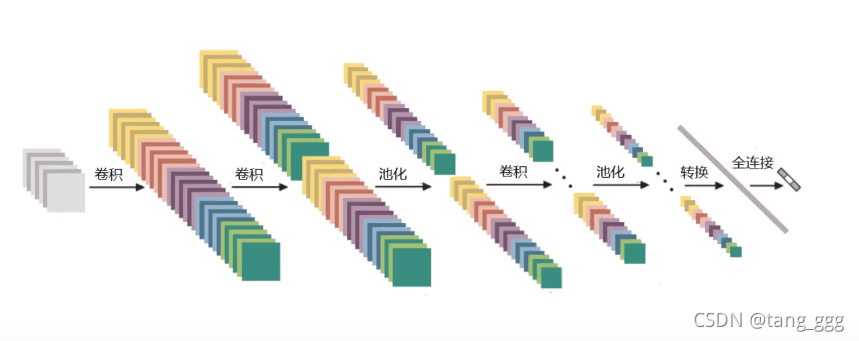
卷积神经网络应用领域

1. 检测任务
2. 追踪任务
3. 分类检索
4. 超分辨率重构
5. 医学任务
6. 无人驾驶
7. 人脸识别

卷积的作用

卷积神经网络与传统网络区别

传统神经网络（nn）

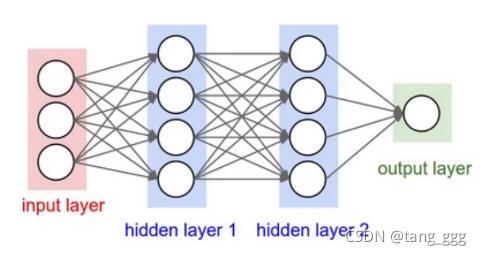
特征是二维的

CNN

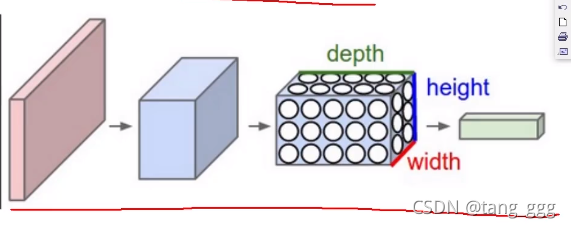
特征是三维的，直接输入原始数据

卷积神经网络的整体架构

1. 输入层
2. 卷积层
3. 池化层
4. 全连接层

输入层

图像数据，例如：28x28的数据

卷积层

提取特征

计算过程

将图像进行一个分割，分成多个小块，目的是在不同的区域，得到的特征不一样。

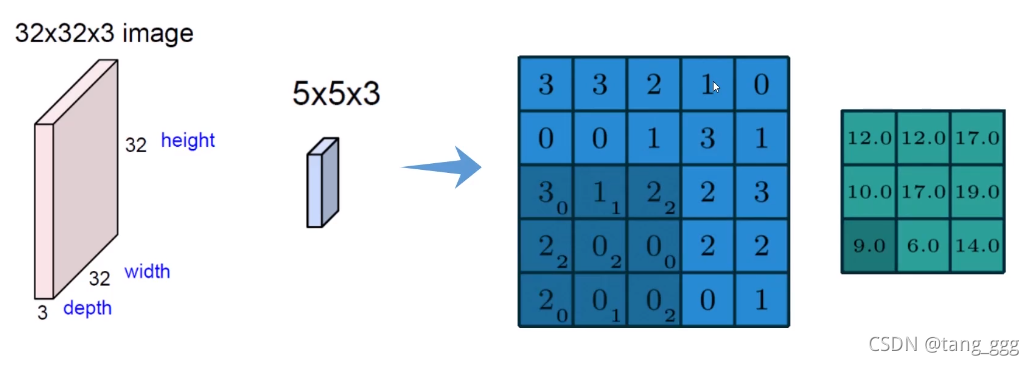
卷积特征值计算方法

图像颜色通道

一张图是三维的，分为R,G,B三个通道分别单独做，之后再加在一起。

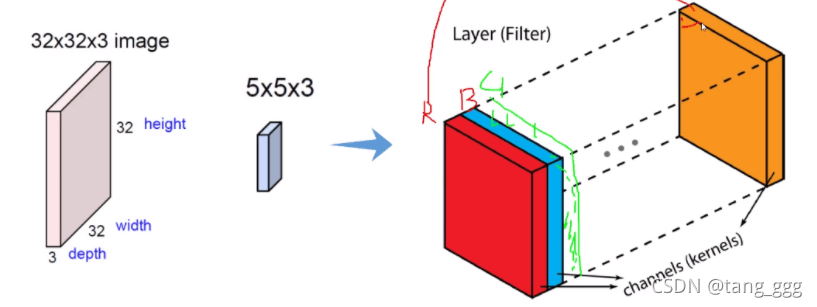
图中Filter（3 x 3 x 3）前两个参数表示的是卷积核的长和宽（规格），第3个表示层数，层数要和进行计算的数据层数相同，下面的 b 是一个偏置的值，最后得到后面绿色方格的值（特征图）

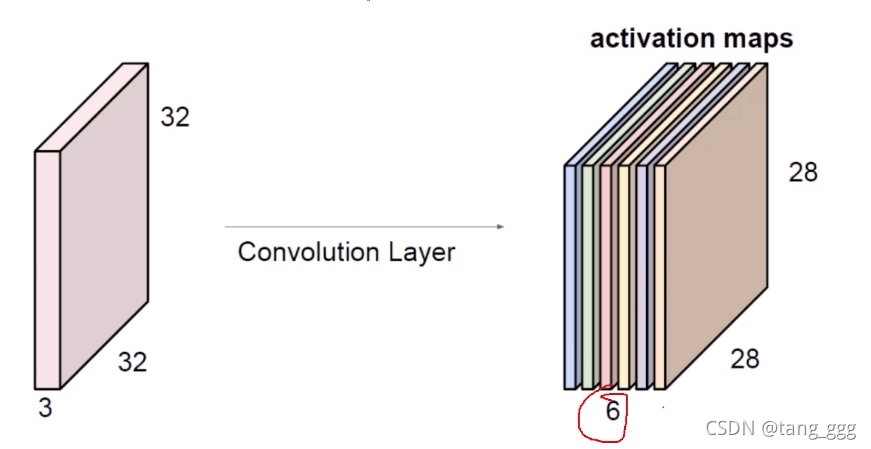
这里使用了两个卷积核（Filter），得到了两个特征图。

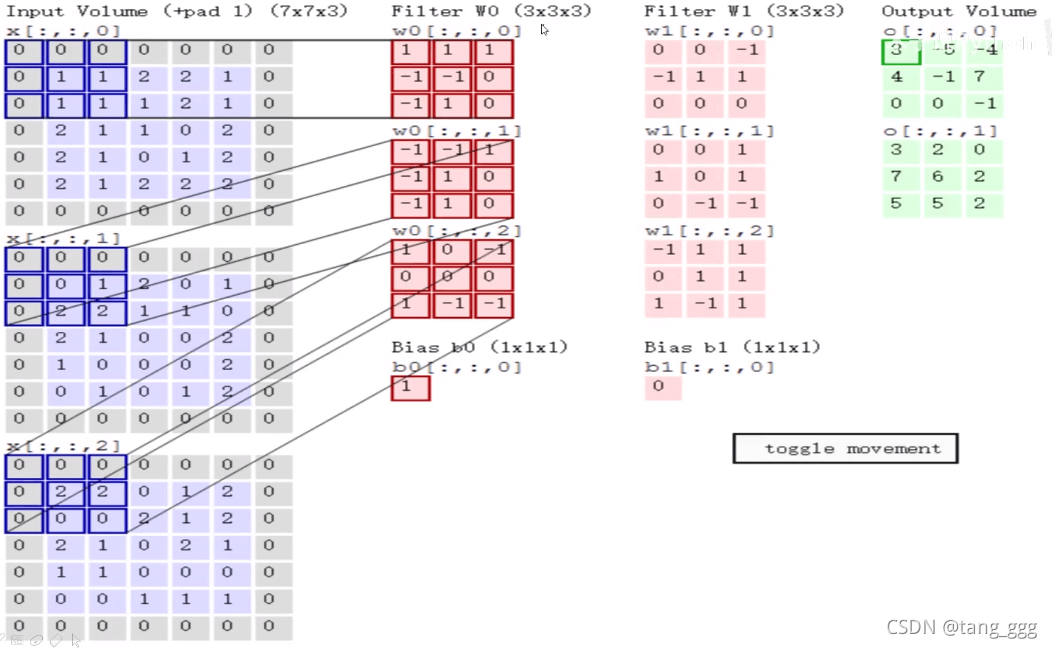
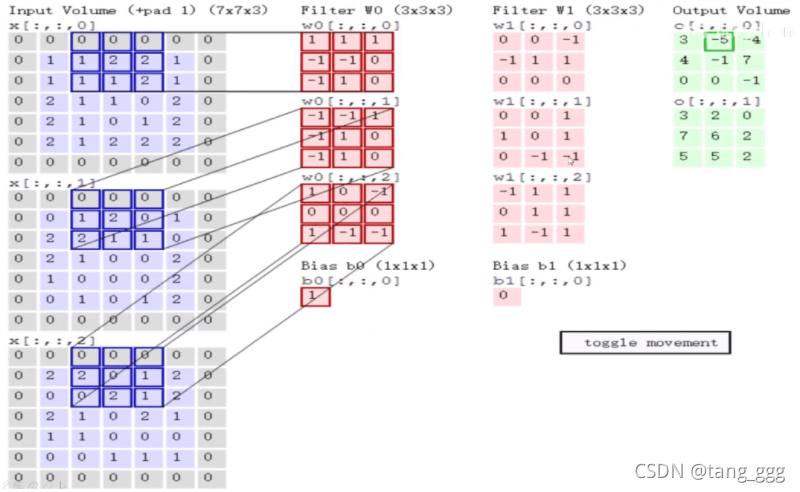
左边第一列数据，矩阵，移动2个单元格，然后重复上面的计算方法。

特征图个数

可以通过用多个Filter对一个地方进行特征提取，可以让我们的特征结果更加的丰富。

下图用不同的卷积核（f1，f2…）计算分别得到两个特征图、六个特征图。

步长与卷积核大小对计算结果的影响

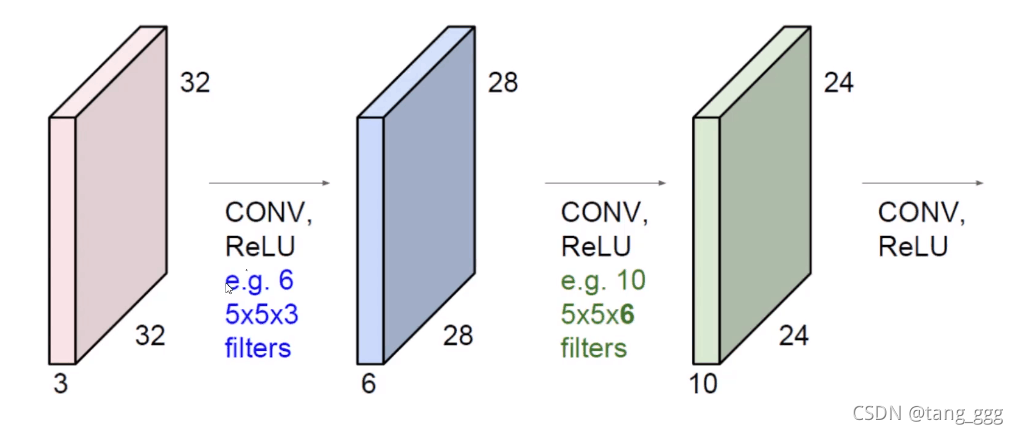
只做一次卷积是不够的，需要多次卷积，如下图，从左到右依次做了多次卷积，每一次的质量是不断增加的。

如下图，第一次用了6个卷积核，下一层则得到6张特征值，对这6张特征值再卷积…直到循环多次结束。

卷积层涉及参数

1. 滑动窗口步长

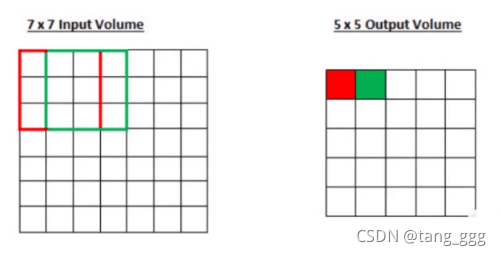
   步长为1的卷积

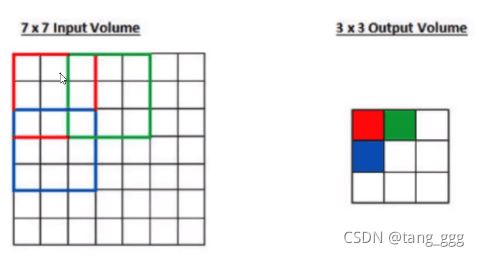
步长为2的卷积

2. 卷积核尺寸

   步长越小得到的特征值越多，越丰富。

3. 边缘填充

   前面可以发现，输入图像与卷积核进行卷积后的结果中损失了部分值，输入图像的边缘被“修剪”掉了（边缘处只检测了部分像素点，丢失了图片边界处的众多信息）。这是因为边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外。

   有时我们还希望输入和输出的大小应该保持一致。为解决这个问题，可以在进行卷积操作前，对原矩阵进行边界填充（Padding），也就是在矩阵的边界上填充一些值，以增加矩阵的大小，通常都用“0”来进行填充的。

4. 卷积核个数

   最后计算中要用到几个特征值就用几个卷积核。

卷积结果计算公式

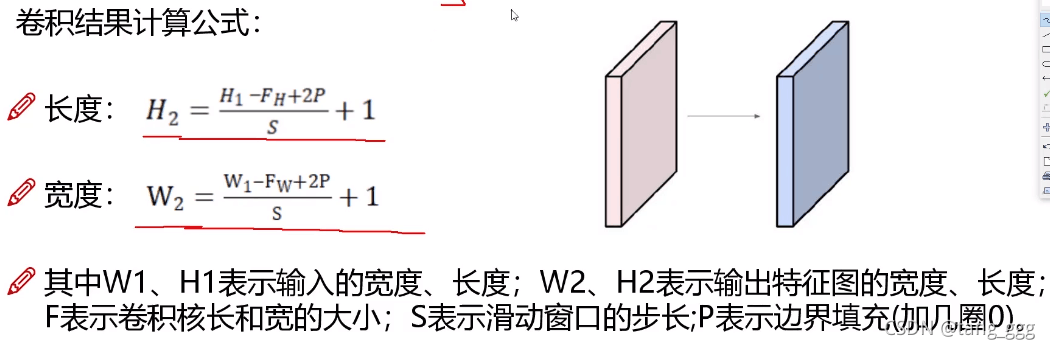
例如：

卷积参数共享

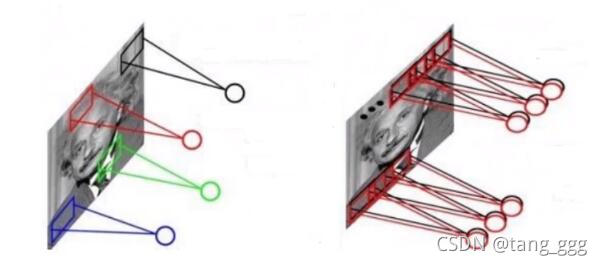
例如：

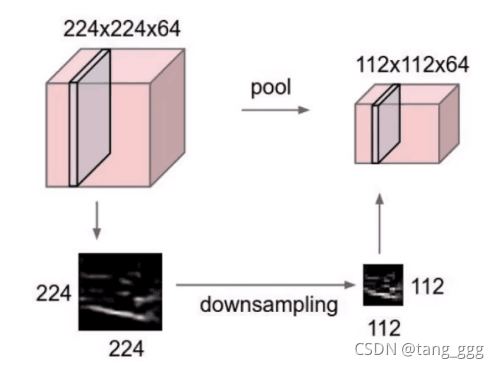
池化层

只是筛选，过滤，没有计算，只能做缩减，不会改个数。

这种机制能够有效地原因在于，在发现一个特征之后，它的精确位置远不及它和其他特征的相对位置的关系重要。池化层会不断地减小数据的空间大小，因此参数的数量和计算量也会下降，这在一定程度上也控制了过拟合。

1. 特征值不变：池化操作是模型更加关注是否存在某些特征而不是特征具体的位置。其中不变形性包括，平移不变性、旋转不变性和尺度不变性。
2. 特征降维（下采样）：池化相当于在空间范围内做了维度约减，从而使模型可以抽取更加广范围的特征。同时减小了下一层的输入大小，进而减少计算量和参数个数。
3. 在一定程度上防止过拟合，更方便优化。

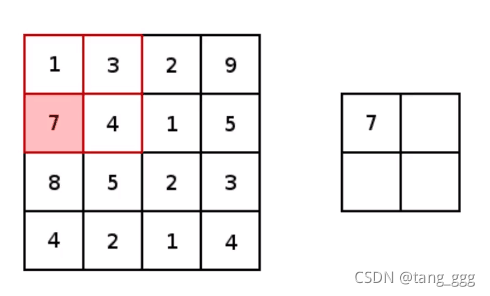
最大池化

选择不同的区域，取出最大的值。（只选大的，选最重要的）

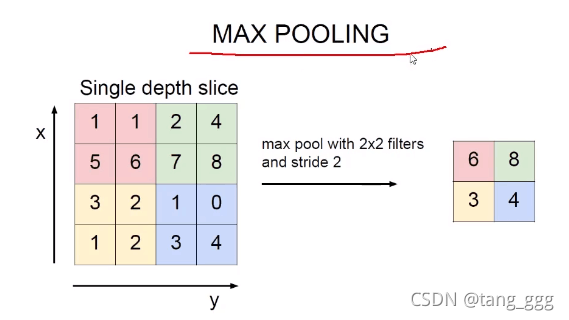
如何运作的

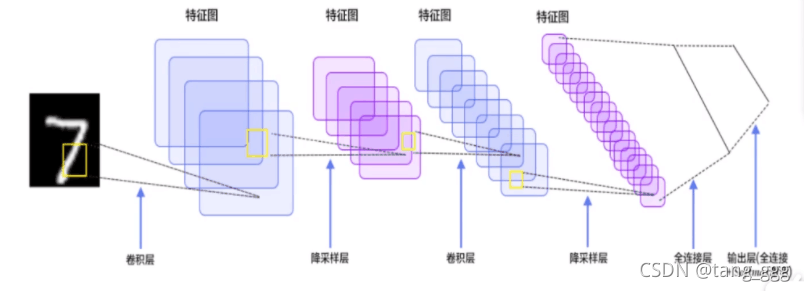
两次卷积一次池化，每个卷积后，都有一个激活函数。

经过卷积、池化的计算和特征提取后，在全连接层实现特征分类。

将生成的三维图，变成特征向量，放入全连接层，下图中被分为5类，后面参数就是5。

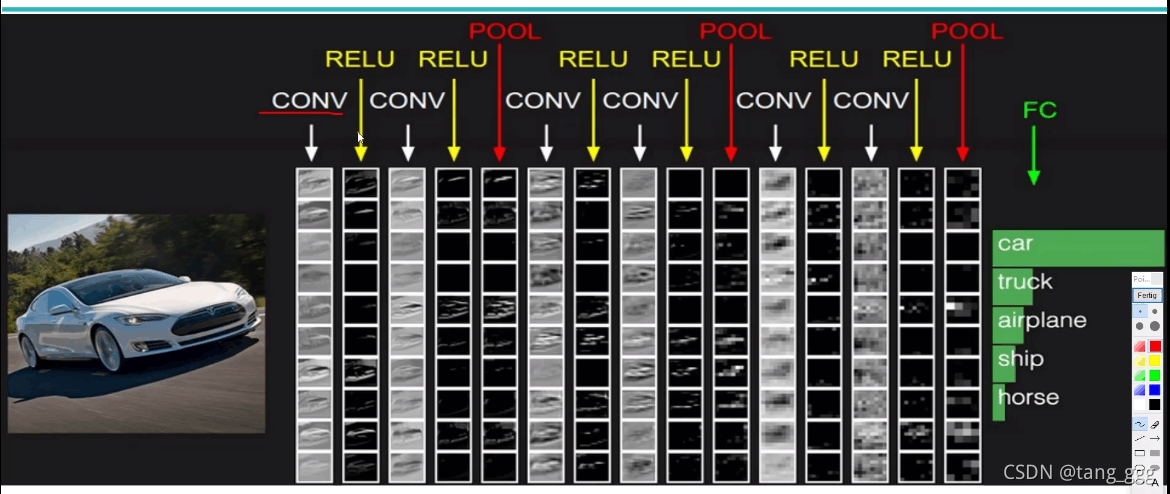
带参数计算的才能称为一层神经网络，卷积层带，激活函数不带，池化层不带，全连接层带。

上图有7层神经网络。

特征图变化

转换：将一个三维的物体转换为向量，才能实现分类。

参考：【计算机博士唐宇迪居然半天教会了我4年没学会的计算机视觉】