abstract

本文提出了针对于图结构数据的模型：diffusion-convolutional neural networks（DCNN）。本文展示了如何通过图结构数据学习到基于传播的数据并被有效用于节点分类。DCNN有很多优秀的特质：图结构的潜在表征在同构的情况下是不变的，计算过程可以被视为可以在多项式时间下完成的向量操作，并能够被有效扩展到GPU之上。通过实验证明，DCNNs在关系节点分类任务上超越了概率关系模型以及图上的核方法。

1.introduction

处理结构数据很具有挑战性。一方面，如果能够有效表达以及挖掘数据结构那么能够提升预测性能，另一方面，找到这样的表征可能很困难，会给预测增加很大的复杂度。

本次工作的目标是设计一个灵活的模型来处理结构数据，它在保持了计算简洁性的同时提升了模型的预测性能。为了达成这些目标，我们通过引入“diffusion-convolution”操作来将CNN扩展到普通的图结构数据上。“diffusion-convolution”在图结构的输入里的每个节点上进行一个diffusion操作来建立潜在表征。

本文的模型的灵感来自于压缩了图传播的表征能够比图本身提供一个更好的预测偏好。图传播（graph diffusion）可以被视为是一个矩阵乘方序列，为包含了内容信息的实体提供直接的机制来可以在多项式时间内被计算以及可以很好地被应用到GPU上。

作为一个模型类，DCNNs具有以下这些优点：
1.准确度：对于图分类任务和节点分类任务超越了其他的迭代模型。
2.灵活性：DCNNs为图数据提供了灵活的表征来编码节点特征、边特征以及单纯的结构信息（在只有很少的预处理的情况下）。DCNNs可以应用于各种图上的分类任务：包括节点分类任务以及全图分类任务。
3.速度：DCNN的预测可以被视为是多项式时间的向量操作序列，可以使用标准库来完成在GPU上的高效率的计算。

2.model

首先做一些问题的符号定义：
T个图的集合 $G=\{G_t|t\in 1,...T\}$ 。每个图 $G_t=(V_t,E_t)。$ 顶点集合被特征矩阵 $X_t$ 刻画，维度为 $N_t \times F$ ， $N_t$ 代表了节点的总数，邻接矩阵 $A_t$ ,维度为 $N_t \times N_t$ ，根据邻接矩阵我们能够计算出一个转移矩阵 $P_t$ ，它定义出了在图上的节点 $i$ 跳跃到节点 $j$ 的概率（有多大可能两个节点之间发生转移，那肯定是路径越多转移可能性越大）。 $G_t$ 可能为有向图/无向图，有权图/无权图。节点或者是图具有labels $Y$ 。

我们本次的任务是预测 $Y$ ,就是说，去预测图中每个节点或者是图本身的标签。在具体情况下，就是我们已知一些有标签的实体，去预测剩下没有标签的实体。如果 $T = 1$ ,标签 $Y$ 是关于图上的节点的话，问题就可以被刻画为半监督分类。如果 $T > 1$ ,每个图都有标签 $Y$ 的话，这就代表了有监督的图分类任务。

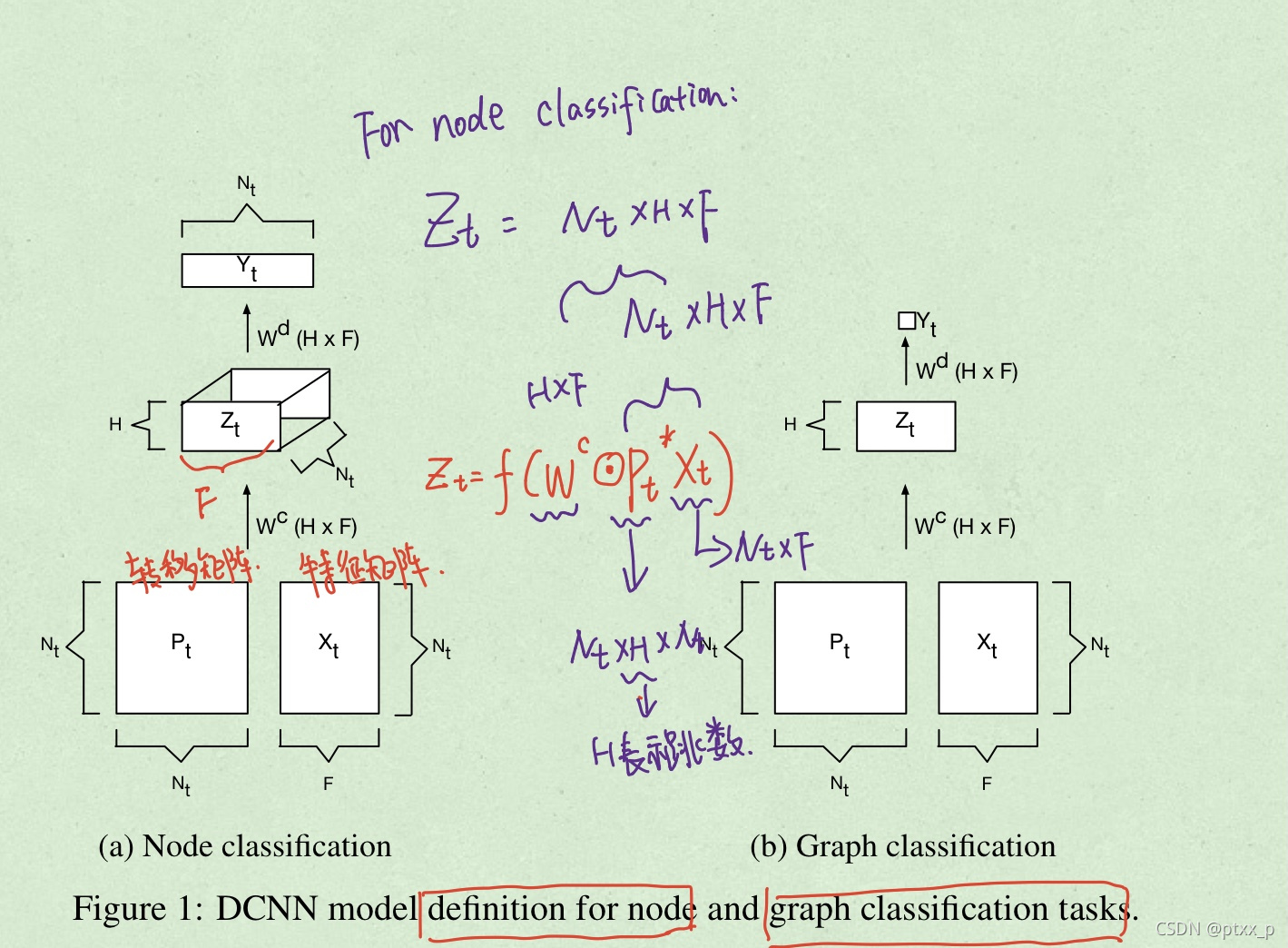
DCNNs可以解决以上提到的所有任务，可以选择返回 $Y$ 的hard 预测，或者conditional distribution $\mathbb{P}(Y|X)$ 。节点或者是图的实体被转化为一个传播卷积表征（diffusion-convolutional representation），本质上是一个 $\times F$ 的实值矩阵，通过在F个特征上的H-hop的图传播形成。这种图传播的过程通过一个 $\times F$ 的实值权重矩阵 $W^c$ 以及非线性可积函数 $f$ 作为激活函数计算得到。所以对于节点分类任务，图 $t$ 的传播卷积表征 $Z_t$ ,会是一个 $N_t \times H \times F$ 的向量（因为共有 $N_t$ 个节点）。而对于图分类任务来说 $Z_t$ 会是一个 $\times F$ 的矩阵。

模型基于传播核的思想，这种思想可以被视为是度量一个图上的两个节点之前的连通性的方式（通过考虑两个节点之间的所有路径），具有更短路径考虑的权重应该更大。传播核为节点分类任务提供了一个很有效的基础。

术语“diffusion-convolution”旨在唤起特征学习、参数绑定和不变性是卷积神经网络的特征。 DCNN 的核心操作是从节点及其特征到到从节点开始的传播结果的映射。与标准的CNN不同，DCNN的参数与传播搜索深度绑定而非是与矩阵中的位置固定。传播卷积表征根据节点的index不变而非根据位置，这就意味着两个同构图的表征将是一致的。和CNN不同，DCNN没有pooling操作。