[人工智能]统计学习方法（一） 感知机(Perceptron)

感知机是二分类的线性分类模型，属于非概率模型，判别模型。是神经网络和支持向量机的基础。

一、感知机模型

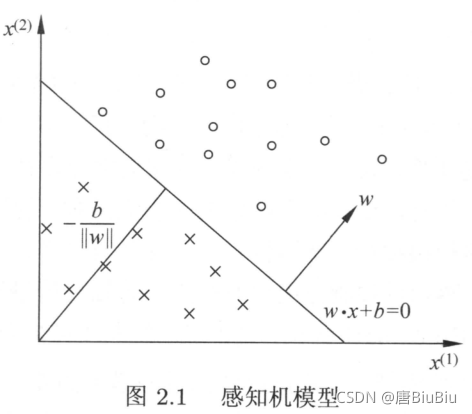
如上图，我们如果能用一条直线将两类不同的样本区分开，那么再拿到一个新的样本，我们就可以根据这条直线的位置将新样本分类。

因此我们的目标就是找到这样的一条线$(w?x+b)$,那么用$$f(x)=sign(w?x+b)$$就可以实现分类的目的。

当然，这里说的是二维的情况。拓展到三维，这条线就变成了一个平面。因此我们将$(w?x+b)$称为超平面（hyperplane）。$w$是超平面的法向量（垂直于平面的直线代表的向量）。$b$是超平面的截距。

二、感知机学习策略

对于一个数据集$T$，如果存在一个超平面能将所有样本完全正确的划分到超平面的两侧，则称$T$为线性可分数据集（linearly separable dataset）,反之则为线性不可分。

若训练集为线性可分的，最直接的目标就是找到能将所有样本完全正确分类的超平面，也就是找到感知机的模型参数$w,b$。为此需要确定一个损失函数（Loss function），并将其最小化。

损失函数选择误分类点到超平面$S$的总距离：

$$\frac{1}{||w||}|w?x_0+b|$$

$||w||$是$w$的L2范数

对于误分类的数据$(x_i,y_i)$有：$?y_i(w?x+b)>0$,因$(x_i,y_i)$到超平面$S$的距离为

$$?\frac{1}{||w||}{y}_i(w?x_0+b)$$

那么所有误分类样本到超平面$S$总距离为

$$?\frac{1}{||w||}\sum _{x_i\in M}^{y_i(w?x_0+b)}$$

不考虑$$?\frac{1}{||w||}$$就得到感知机学习的损失函数$L(w,b)=?{\sum }_{x_i\in M}^{y_i(w?x_i+b)}$（经验风险函数）

其中$M$为误分类样本的集合。

显然损失函数是非负的。分类点越少，误分类点离超平面越近，损失函数越小。分类完全正确时损失函数为0.

三、感知机学习算法

感知机学习算法是误分类驱动的，具体采用随机梯度下降法（stochastic gradient descent）。这个过程中不是一次使$M$中所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

假设误分类点集合$M$是固定的，那么损失函数$L(w,b)$的梯度：

${?}_{w}L(w,b)=?{\sum }_{x_i\in M}^{y_i{x}_i}$

${?}_{b}L(w,b)=?{\sum }_{x_i\in M}^{y_i}$

随机选取一个误分类点$(x_i{y}_i)$,对$(w,b)$更新：

$w\leftarrow w+\eta y_i{x}_i$

$b\leftarrow b+\eta y_i$

其中$\eta$是学习率（0<$\eta$<1）

实操（torch）

使用mnist数据集，为了方便，首先将数据集转化为JPG格式（代码就不放了，不重要），标签在文件名上。

以下代码为感知机的代码。经过测试，我发现训练集完全不用给定的6W张照片，我只取了2000张训练，就达到了测试集100%的准确率。这也证明了mnist数据集是线性可分数据集。实验结果在最后。

import os
import torch
import time
from torch import tensor
import cv2
import numpy


def loaddata(jpgpath):
    '''
    读取数据
    '''
    print('read data...')
    itemlist = os.listdir(jpgpath)
    item = []
    label = []

    for i in itemlist:
        img = torch.from_numpy(cv2.imread(f"{jpgpath}/{i}",0).reshape(28*28,-1))
        item.append(img.float())
        label.append(-1 if int(i.split('.')[0][-1])<5 else 1)

    return item,label


def perceptron(item,label,lr=0.0001,iter=50):
    '''
    训练过程
    '''
    m = len(item)
    n = 784
    w = torch.zeros([1,n])
    b = 0.

    for k in range(iter):
        for i in range(m):
            x = item[i]
            y = label[i]
            # print(torch.mm(w,x))
            a = -1*y*(torch.mm(w,x)+b)[0][0]
            if a>=0:
                w = w + lr*y*x
                b = b + lr*y
        print(f'Round {k}/{iter} trianing')

    return w,b


def test(item,label,w,b):
    '''
    测试过程
    '''
    m = len(item)
    label_perd = []
    for i in range(m):
        x = item[i]
        y = label[i]
        if y * (torch.mm(w,x) + b)[0][0] > 0 :
            label_perd.append(1)
        else:
            label_perd.append(-1)

    right = 0
    for i in range(m):
        if label_perd[i] == label[i]:
            right += 1
    
    return right/m


if __name__ == "__main__":
    start = time.time()

    item,label = loaddata('train_images')
    w,b = perceptron(item,label)
    # print(f'w:{w},b:{b}')
    item,label = loaddata('test_images')
    print(f"正确率：{test(item,label,w,b)}")
    end = time.time()

    print(f'所需时间：{end-start}')