[人工智能]知识图谱论文阅读（十六）【AAAI2020】Knowledge-Enhanced Top-K Recommendation in Poincaré Ball

题目： Knowledge-Enhanced Top-K Recommendation in Poincaré Ball
论文链接：
代码链接：

想法

创新点

摘要

目标是更有效的利用KG，提出了一个双曲空间，可以便于学习这知识图的层次结构！
具体而言，是给KG的关于某个item的邻居增加了双曲注意力网络，此外，提出了一种自适应和细粒度的正则化机制，以自适应正则化项目及其邻近表示。

引入

将KG嵌入推荐系统中，有两种方法： Path-based和正则化方法。 path-based的可以携带高阶的连接信息，同时选取路径时要么人工，要么定义路径选取模型。但是基于正则化的方法则是设计捕捉KG结构的额外损失terms，并使用这些terms使推荐模型学习正则化。

以前方法的缺点： 首先，之前的作品都是在欧几里得空间学习KG的表示，这可能无法有效捕获已知存在于KGs的层次结构！ 其次，CKE、CFKG和RippleNet等方法在学习每个实体的表示时，并没有区分相邻实体，而是根据它们的相对重要性和信息性进行调整。 这可能导致不良的模糊信息的关系和实体不完整的理解；第三，所有的正则化的方法则会采用一个固定的参数。 我们认为正则化的程度应该是自适应的，应该根据从知识图中

Preliminaries

Problem Formulation

隐式反馈由若干user-item pairs表示， $\mathcal{D}=(u,v)?\mathcal{U}\times I$，其中$\mathcal{U}$是用户集合，$\mathcal{I}$是item集合，item知识图谱$\mathcal{G}=(h,r,t)?\mathcal{E}\times \mathcal{R}\times \mathcal{E}$能被表述成一组三元组，一个关系两个实体。 头和尾。

本文的Top-K推荐任务：给定用户$u$的训练item集合$S_u$，用户$i$的非空训练item set${\mathcal{T}}_u$（要求${\mathcal{S}}_u\cup {\mathcal{T}}_u={\mathcal{D}}_u$）和 ${\mathcal{S}}_u\cap {\mathcal{T}}_u=?$，模型必须推荐一组有序的项目${\mathcal{X}}_u$，其中$\left|{\mathcal{X}}_u\right|\le K$和${\mathcal{X}}_u\cap {\mathcal{S}}_u=?$，然后通过${\mathcal{T}}_u$和${\mathcal{X}}_u$之间的匹配评分来评估推荐的质量，比如Recall @$K$

Poincaré Ball的双曲几何

Poincaré球模型是双曲几何(Cannon et al. 1997)的五个等距模型之一，双曲几何是具有恒定负曲率的非欧几里得几何，正式上，

两点之间的距离$\mathrm{x},\mathrm{y}\in {\mathbb{B}}^d$是沿测地线(即两点之间的最短路径)测量的，由:

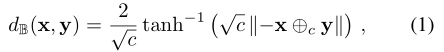
其中$\Vert ?\Vert$表明了欧几里得norm，并且${\oplus }_c$代表M?bius addition(Ganea, Bécigneul, and Hofmann 2018)

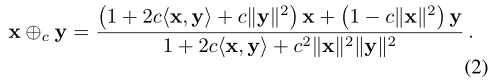
Methodology

在本节中，我们将介绍提出的模型HyperKnow，它将知识图与双曲空间中的推荐任务结合在一起。首先介绍了双曲空间中的用户偏好学习，然后使用双曲注意机制来区分KG中的item的邻居实体。接下来，我们解释了如何通过一个双层优化公式自适应地学习被推荐的内容和知识图。最后介绍了该模型的训练和预测过程。

Learning User Preference