hi各位大佬好,关于ytb可谓是无人不知无人不晓,这个玩意必然也是应知应会的题目,这是基本的问题,与FM是一样的。
For Recommendation in Deep learning QQ Second Group 102948747
For Visual in deep learning QQ Group 629530787
I'm here waiting for you?
不接受这个网页的私聊/私信!!
本宝宝长期征集真实情感经历(发在我公号:美好时光与你同行),长期接受付费咨询(啥问题都可),付费改代码。
付费咨询,专属服务,快人一步!!!
1-关于序列推荐的本质
序列推荐在本质上也是多对多问题,由多个点击的item预测未来要点击的多个item,这就是seq2seq。在翻译中不也是如此么??
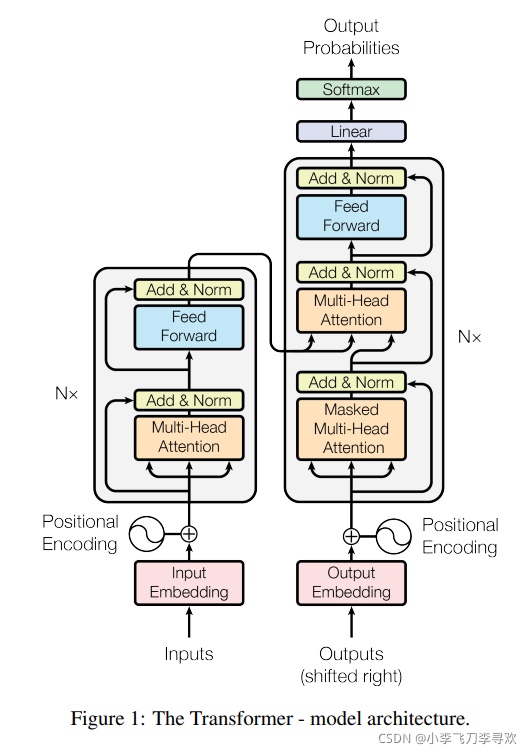
?2-几个函数
2.1tf-function中的input_signature
>>> @tf.function
... def f(x):
... return x + 1
>>> vector = tf.constant([1.0, 1.0])
>>> matrix = tf.constant([[3.0]])
>>> f.get_concrete_function(vector) is f.get_concrete_function(matrix)
False
>>> @tf.function(
... input_signature=[tf.TensorSpec(shape=None, dtype=tf.float32)])
... def f(x):
... return x + 1
>>> vector = tf.constant([1.0, 1.0])
>>> matrix = tf.constant([[3.0]])
>>> f.get_concrete_function(vector) is f.get_concrete_function(matrix)
True
get_concrete_function(*args, **kwargs) method of tensorflow.python.eager.def_function.Function instance
Returns a `ConcreteFunction` specialized to inputs and execution context.
If this `Function` was created with an `input_signature`, `args` and
`kwargs` may be omitted. With an input signature there is only one
concrete function associated with this `Function`.
An "input signature" can be optionally provided to `tf.function` to control
the graphs traced. The input signature specifies the shape and type of each
Tensor argument to the function using a `tf.TensorSpec` object. More general
shapes can be used. This is useful to avoid creating multiple graphs when
Tensors have dynamic shapes. It also restricts the shape and datatype of
Tensors that can be used:?只要输入上面的参数(shape及数据类型),那么就是指定同一个function,
2.2-rsqrt开根号后求倒数
>>> tf.math.rsqrt([3.0,0,-4.0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.57735026, inf, nan], dtype=float32)>
>>> tf.math.sqrt([3.0,0,-4.0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([1.7320508, 0. , nan], dtype=float32)>
>>> 1/tf.math.sqrt([3.0,0,-4.0])
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.57735026, inf, nan], dtype=float32)>
负数开根号为非数,非数的倒数还是非数。
2.3-增加两个维度expand_dims
>>> k
<tf.Tensor: shape=(3, 4), dtype=float32, numpy=
array([[-0.19508752, -0.24705486, -1.4569125 , -0.48979878],
[ 0.3164492 , -0.01150408, 0.45663917, -0.8849148 ],
[ 0.31029478, -1.5752182 , 1.4130656 , 0.41960722]],
dtype=float32)>
tf.expand_dims(k,[-1])
#这个用两次啊
或者
>>> k2=k[:,:,tf.newaxis,tf.newaxis]
>>> k2.shape
TensorShape([3, 4, 1, 1])
3-multi-head-attention多头attention
如果是一个头,那就是常规的attention,多个头只是增加了多个q,k,v,仅此而已。
如果单纯用多头attention是可以进行增加维度(比如dense操作)的,但如果要加残差结构,那么就必须保证维度一致,不然没法加啊。
>>> mat=MultiHeadAttention(d_model,num_heads)
>>> x.shape
TensorShape([12, 10, 16])
>>> res=mat(x,x,x,mask)
>>> res.shape
TensorShape([12, 10, 32])
>>> d_model
32
>>> num_heads
2
Encoder单层,即最上图的左边,
>>> model=EncoderLayer(num_heads,x.shape[-1],dense_dim)
>>> res=model(x,True,mask)
>>> res.shape
TensorShape([12, 10, 16])
>>> x.shape
TensorShape([12, 10, 16])
3.1-由于mask采用的是下面的形式与常见的mask可能相反,
self.masks = 1- tf.tile(mask[:,:,tf.newaxis,tf.newaxis],[1,1,self.seq_len,self.num_heads])
然后就用了一层encoder,此时仍旧比上次的最佳要差一点
item_his_eb = self.encoder(item_his_eb,True,self.masks)
item_his_eb = self.dense3(tf.transpose(item_his_eb,[0,2,1]))
self.user_eb = tf.squeeze(item_his_eb)
[0.05438987 0.28721324 0.05550319 0.09987947 0.01372705]3.2-当mask采用原来的mask(仅仅修改上面的mask,其他不改),那么如下,似乎没多大影响啊
self.masks = tf.tile(mask[:,:,tf.newaxis,tf.newaxis],[1,1,self.seq_len,self.num_heads])
[0.0543663 0.2829085 0.04441036 0.09898286 0.01082832]3.3-在3.1的基础上去掉刚开始的mask,效果变差
item_his_eb = item_list_add_pos#tf.multiply(item_list_add_pos,tf.expand_dims(mask, -1))#[B,maxlen,dim]
[0.05211236 0.27617246 0.0436714 0.09578644 0.01040524]3.4-在3.1的基础上去掉mask,反而是目前最佳的结果,说明mask在attention中没啥用啊
item_his_eb = self.encoder(item_his_eb,True,None)#self.masks)
item_his_eb = self.dense3(tf.transpose(item_his_eb,[0,2,1]))
self.user_eb = tf.squeeze(item_his_eb)
[0.05593012 0.2944682 0.06165472 0.10250784 0.01543112]4-聚合方式
我感觉从上面的试验及之前的试验,最终决定效果天花板的应该是最后一步的dense或者说pooling
这种目前暂时没有想到特别有效的聚合方式。
因此先试试gap吧,其实与mean是没有区别的。
在3.4的基础上换成gap,竟然取得最佳的结果,卧槽,那么是不是把位置信息也给平均了?
[0.0581151 0.31083053 0.09423887 0.10766441 0.02585611]因此将位置编码去掉,结果稍微差点,说明pooling还是可以的
[0.05645998 0.30347934 0.08502831 0.10482394 0.02255137]如果不去掉位置,而是将pooling换成mean,那么效果又提高了,haha
[0.05937547 0.3134265 0.09733415 0.10924349 0.02662534]那么这就有一个问题摆在面前,一维pooling与mean有啥区别么?pooling有训练的参数么?而且pooling得到的结果在faiss计算时相当慢(pooling 3s,mean-1s)
然而经过测试发现,两者结果是一样的,对于指标不同,可能是训练过程的问题,因为本就相差不大,基本上可以忽略。但对于faiss计算的快慢,我不知道咋解释了。
>>> x0=tf.random.normal([13,10,18])
>>> x0.shape
TensorShape([13, 10, 18])
>>> x2=tf.keras.layers.GlobalAveragePooling1D()(x0)
>>> x3=tf.math.reduce_mean(x0,1)
>>> np.array_equal(x2.numpy(),x3.numpy())
True
>>>
按照旧版YouTube再试下聚合方式,以及参考其取mean方式,如下,
?在本文最优的基础上发现效果更差了,woc【我怀疑是user_id搞错了,但搞错的话应该没这么高的指标啊】,这个指标与此博文对应,都是差不多的数值
item_his_eb = self.encoder(item_his_eb,True,None)
tmp = tf.concat([tf.nn.embedding_lookup(self.uid_embeddings_var,user_t1),tf.math.reduce_mean(item_his_eb,1)],axis=-1)
self.user_eb = self.dense2(tmp)
[0.03897376 0.23201779 0.05910321 0.07654342 0.01505933]直接相加的结果也不太行,
self.user_eb = tf.nn.embedding_lookup(self.uid_embeddings_var,user_t1)+tf.math.reduce_mean(item_his_eb,1)
[0.03621471 0.24466549 0.06938735 0.07664543 0.01780289]?相乘呢?。。。
[0.02392878 0.16216457 0.01828449 0.05056945 0.00450191]?既然如此,将旧版本ytb再改为新版本的聚合模式,试试,没啥提高,到此为止吧。
[0.04446743 0.24024637 0.01803327 0.08255393 0.00387843]5-多层Encoder
用多层的时候报错了,如下,这是啥玩意啊。
ValueError: Weights for model sequential_1 have not yet been created. Weights are created when the Model is first called on inputs or `build()` is called with an `input_shape`后来发现是加了dropout的原因,但为啥呢?加上了input_shape还是不对,这个暂时不要吧,哈哈
两层Encoder结果并没有提高,如下,
[0.0585502 0.3106855 0.09285575 0.10797357 0.02531075]三层也是差不多的结果,不再附。
