一、机器学习(深度学习)中的数学基础
1.线性代数:数据表示、空间变换的基础。
2.概率论(统计):模型假设、策略设计的基础。
3.最优化:求解目标函数的具体算法。
4.信息论:对于不确定性的度量,信息增益选择特征,交叉熵。
5.微积分:链式求导,泰勒展开。
6.矩阵线性变换,矩阵相乘对原始向量同时施加方向变化和尺度变化。对于特征向量,矩阵的作用只有尺度变化而没有方向变化。尺度变化系数就是特征值。
7.线性代数:秩
-
线性方程组的角度:度量矩阵行列之间的相关性。
-
数据点分布的角度:表示数据需要的最小的基的数量。
(1)数据分布模式越容易被捕捉,即需要的基越少,秩就越小。
(2)数据冗余度越大,需要的基就越少,秩越小。
(3)若矩阵表达的是结构化信息,如图像、用户-物品表等,各行之间存在一定相关性,一般是低秩的。
8.数据降维,奇异值分解,较大奇异值包含了矩阵的主要信息。
9.低秩近似,其意义保留决定数据分布的最主要的模式/方向(丢弃的可能是噪声或其他不关键信息)。比如:推荐系统,图像去噪等。

二、机器学习三要素:模型、策略、算法
(一)概率/函数形式的统一
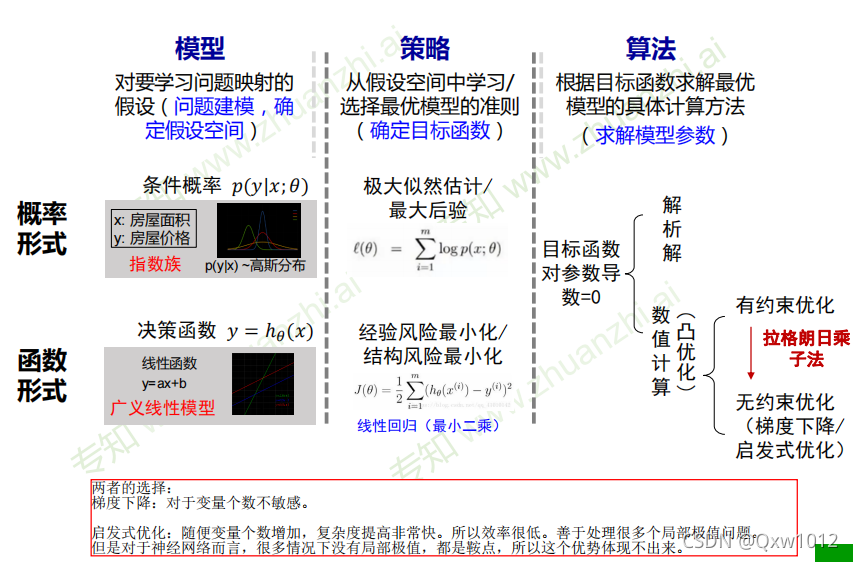
(二)“最优”的策略设计
-
策略目标:训练误差小 & 泛化错误低
-
策略设计: 无免费午餐定理,脱离具体问题,谈‘什么学习算法更好’ 毫无意义 (周志华),也就是说没有任何一个模型可以在所有的学习任务里表现最好。
-
策略设计: 奥卡姆剃刀原理,如果多种模型能够同等程度地符合一个问题的观测结果,应该选择其中使用假设最少的,也就是最简单的模型。
-
欠拟合:训练集的一般性质尚未被学习器学好,(训练误差大)。
解决方法:提高模型复杂度
● 决策树:拓展分支
● 神经网络:增加训练轮数 -
过拟合:学习器把训练集特点当做样本的,一般特点. (训练误差小,测试误差大)。
解决方法:降低模型复杂度
● 优化目标加正则项
● 决策树:剪枝
● 神经网络:early stop、dropout
● 数据增广(训练集越大,越不容易过拟合)。计算机视觉:图像旋转、缩放、剪切;自然语言处理:同义词替换;语音识别:添加随机噪声。
(三)损失函数
- 平方损失函数(回归)。
L ( y , y ^ ) = ( y ? f ( x , θ ) ) 2 L(y,\hat y)=(y-f(x,\theta))^2 L(y,y^?)=(y?f(x,θ))2 - 平均绝对值损失-L1损失(回归)
M A E = ∑ r = 1 n ∣ y i ? y i p ∣ MAE=\sum_{r=1}^n|y_i-y_i^p| MAE=r=1∑n?∣yi??yip?∣
- 交叉熵-对数损失函数(分类)。
H ( p , q ) = ? ∑ r = 1 n p ( x i ) l o g ( q ( x i ) ) H(p,q)=-\sum_{r=1}^np(x_i)log(q(x_i)) H(p,q)=?r=1∑n?p(xi?)log(q(xi?)) - 0-1损失函数(分类)。
L ( Y , f ( X ) ) = { 0 , Y?=?f(X) 1 , Y? ≠ ?f(X) L(Y,f(X)) = \begin{cases} 0, & \text{Y = f(X)} \\ 1, & \text{Y $\neq$ f(X)} \end{cases} L(Y,f(X))={0,1,?Y?=?f(X)Y??=?f(X)? - hinge loss(分类)
L ( y , f ( x ) ) = m a x ( 0 , 1 ? y f ( x ) ) L(y,f(x))=max(0,1-yf(x)) L(y,f(x))=max(0,1?yf(x))
三、频率学派 & 贝叶斯学派

