重要概念:
1 线性可分:
2 线性不可分:
图1

图2


基于二维特征空间时,有如下定义:

以上间隔确定的直线并不唯一。
支持向量机寻找的最优分类直线应满足的条件:
1 该直线分开了两类
2 该直线有最大间隔
3 该直线处于间隔中间,到所有支持向量距离相等。
线性可分情况下,支持向量机寻找最佳超平面的优化问题可以有如下表述:

在推导之前,有如下两个事实:
1

2
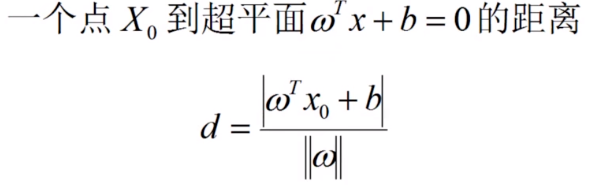
基于上述事实,有如下推导过程:
关键过程1:

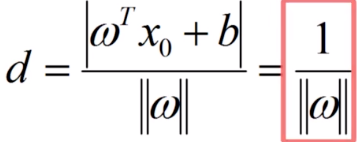
优化问题为求最大的d,转换为求最小的||w||,上述表述中加1/2,是为了后续求导方便。
可以看出这是典型的凸优化问题中的二次规划问题。
关于二次规划问题的定义:
1 目标函数是二次项,(||w||^2)
2 限制条件是一次项, (yi)
凸优化问题只有唯一的全局极值,应用梯度下降算法,可以很方便的求出。
线性不可分情况,对于以上的表述是无解的,即求不出对应的w和b,为此,需要定义松弛函数,对限制条件进行适当放松,以满足求解需要。限制条件可以改成:
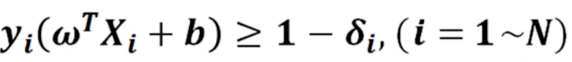
同时需要加入相应限制,防止每个δ无限制扩大。修改后最终如下: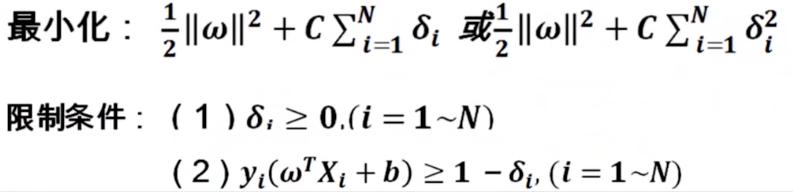
其中,比例因子C是人为设定的(需要人为事先设定的参数称为算法的超参数)。一般会选取不同超参数C,对于每个C,进行算法识别率测试,最终选定能使算法识别率达到最大的超参数C。超参数越多,算法需要手动调整的部分就越多。支持向量机是超参数很少的算法模型。
将训练样本由低维映射到高维可以增加线性可分的概率(有如下假设和定理):

将x映射为φ(x)后,以上描述又可变为: