Note
? 本笔记为笔者自学网课做的一些重要步骤和理解的记录,目的是在需要的时候可以快速回顾,并记录自己学习的一个过程。因此有些内容可能不完整,可以根据自己需求去补充相应的笔记。如果你恰好看到了我的笔记,可以配合慕课网的 《Python3入门人工智能 掌握机器学习+深度学习 提升实战能力》食用,效果更佳。
第一章 导学
1.人工智能实现方法
人工智能实现方法: 符号学习(Symbolic learning)和机器学习(Machine learning)



2.开发环境
开发环境:Python、Anaconda、Jupyter Notebook


3.基础工具包
基础工具包:Panda、Numpy、Matplotlib

4.配置环境
配置环境:下载安装python、anaconda。
在anaconda中,建议每个项目新建一个开发环境,以免造成不必要的冲突。
其中,创建新环境的语句:conda create -n env_name ,激活环境语句:conda activate env_name 。(加粗斜体***env_name***为自定义环境名称)
在新建的环境中安装Jupyter Notebook即可完成环境配置。
5.Jupyter Notebook界面优化
Jupyter Notebook界面优化:由于默认的notebook的显示非常不舒服,所以导入新主题。
-
进入网址: https://github.com/dunovank/jupyter-themes ,找到安装命令pip install jupyterthemes / conda install -c conda-forge jupyterthemes ,在当前环境的命令行下使用pip / conda对应的语句安装该主题包。
由于安装过程比较慢,可以使用一些国内的源。直接百度python源,找到一些国内镜像源:阿里/清华/豆瓣等。修改源的方法:原来的语句 + -i +源的地址,比如 pip install jupyterthemes 修改后变成 pip install jupyterthemes -i https://pypi.tuna.tsinghua.edu.cn/simple/ 。
安装完成后,测试有没有安装好,语句为: jt -h 。如果成功显示了帮助的一些东西,就证明是安好了,当然我们也可以根据帮助来使用主题,如下图。

-
推荐的配置:jt -t grade3 -f fira -fs 13 -cellw 90% -ofs 11 -dfs 11 -T
原先的主题:

现在的主题:

6.开始编码
开始编码:在notebook右上角点new新建python文件,然后在file中重命名即可
- 使用markdown编辑除代码外的内容,换行要在该行结尾处多打两个或以上空格
- 使用markdown编辑完成后运行该cell即可显示运行结果
- ctrl+回车即可快速运行选中cell
7.Python的基础语法及Pandas、Numpy、Matplotlib实操
Python的基础语法及Pandas、Numpy、Matplotlib实操(见basic_coding.ipynb),下载包依旧建议使用国内源
国内源地址
中国科技大学: https://pypi.mirrors.ustc.edu.cn/simple/阿里云: http://mirrors.aliyun.com/pypi/simple/
豆瓣(douban): http://pypi.douban.com/simple/
清华大学: https://pypi.tuna.tsinghua.edu.cn/simple/
中国科学技术大学 :http://pypi.mirrors.ustc.edu.cn/simple/
科大放两个以显示其更好
pip install numpy -i 源地址即可
Matplotlib画图总结
- 导入matplotlib,并导入需要的matplotlib下的对应子包。
- 创建并初始化图对象(包含指定图大小等初始化操作)
- 使用子包方法指定图像名称
- 使用给定坐标及子包相应方法绘图
- 使用子包方法展示图像
eg:使用Matplotlib画个折线图
#使用Matplotlib
import matplotlib
from matplotlib import pyplot as plt
#生成图的实例
fig1 = plt.figure(figsize=(5,5))
#指定图名称
plt.title('My First Matplotlib Chart')
plt.xlabel('x-axis')
plt.ylabel('y-axis')
#给定各点坐标
x = [1,2,3,4,5]
y = [2,3,4,5,7]
plt.plot(x,y)
plt.show()

使用Matplotlib绘制散点图,就把plt.plot改成plt.scatter即可
#使用Matplotlib绘制散点图
import matplotlib
from matplotlib import pyplot as plt
#让图在jupyter中直接展示出来
%matplotlib inline
#给定各点坐标
x = [1,2,3,4,5]
y = [2,3,4,5,7]
#生成图的实例
fig1 = plt.figure(figsize=(5,5))
#指定图名称
plt.title('My First Matplotlib Chart')
plt.xlabel('x-axis')
plt.ylabel('y-axis')
plt.scatter(x,y)
plt.show()

Numpy总结
Numpy的强大之处在于它可以很方便地对数组进行运算,首先要学会使用numpy构建数组,并做简单数组运算,更多运算参考官网文档。
eg:使用numpy生成俩数组,并求和。
import numpy as np
arr1 = np.eye(5)
print(type(arr1))
print(arr1)
#打印该数组维度
print(arr1.shape)

arr2 = np.ones((5,5))
print(type(arr2))
print(arr2)
#打印该数组维度
print(arr1.shape)

res = arr1+arr2
print(type(res))
print(res)
#打印该数组维度
print(res.shape)

Pandas总结
Pandas的强大之处在于它可以很方便地对数据进行加载、保存和索引。
eg1:读取csv文件,并分别索引出 x列对应的所有行数据 和 y列对应的所有行数据。
import pandas as pd
#读取csv文件
data = pd.read_csv('data.csv')
print(type(data))
print(data)

#分别索引x和y对应的所有行
x = data.loc[:,'x']
print(type(x))
print(x)
y=data.loc[:,'y']

eg2: 筛选出x<0 且 y>50的所有行
#索引切片案例:筛选出x<0 且 y>50的所有行
data1 = data.loc[:,'x'][x<0][y>50]
print(data1)

关于loc函数的用法,第一次遇到,查了一下官方文档和博客,发现这个和数据库的思想差不多,就是从所有数据中查找我们需要的子集,无非是写法不同,参考 https://blog.csdn.net/u014712482/article/details/85080864 和 https://www.jianshu.com/p/521f6e302f38。此处涉及python切片知识,特地学了一下,链接:https://www.jianshu.com/p/15715d6f4dad ,可以说是讲的很详细了,看完感觉切片的功能太强大了,以后很多操作方便多了。
最后,在做数据处理的时候会使用Pandas导入csv文件,但是处理起来并不方便,通常会将DataFrame类型转成Numpy类型,方便进行数组间的科学计算。
#常将DataFrame类型转成Numpy类型,方便处理
print(type(data))
np_data = np.array(data)
print(type(np_data))
print(np_data)

对比一下原来的csv文件,看看它的转换过程如何理解。

如图,csv转成numpy类型可以这样理解,由于数组下表具有顺序性,而csv文件的行标签也有顺序性,因此可以省略csv文件的行,直接把所有的行依次排成队列放入一维数组中,最终形成二维数组(python应该叫列表),完成转化过程。
最后关于Pandas,值得注意的是它的存储功能。
在使用Pandas加载文件数据,处理过之后,我们可能需要保存数据,这时使用 to_csv(‘保存路径’) 进行保存
eg: 对用Pandas加载进来data.csv文件的数据全部加15后得到的数据进行展示并保存
#在对数据进行处理后,通过pandas进行数据保存
new_data = data +15
#展示前5行,因为数据特别大的时候没必要全部打开
new_data.head()

new_data.to_csv('new_data.csv')
执行完该语句会发现当前ipynb文件所在目录下多了一个new_data.csv文件,打开得到保存后的数据内容。关于第一列的索引,可以参考官网文档选择性删除。

第二章 机器学习之线性回归
1.机器学习介绍
1.1什么是机器学习?
举个例子:

如图的问题,对于传统算法而言,我们给出1月工资和计算的方程(关系表达式),通过计算机可以帮我们算出结果。而对于机器学习,不需要我们在给出方程(关系表达式)了,只需要给一堆数据,计算机会自己训练出表达式并根据表达式得到结果。这显然要比传统算法更智能。
定义如下:

1.2应用场景

1.3基本框架

1.4机器学习的类别

- 监督学习:告诉计算机哪些是对的数据,哪些是错的数据,再让它训练。
- 无监督学习:不告诉计算机哪些是对的数据,直接让它训练。
- 半监督学习:也叫混合学习,只告诉计算机少量正确的数据,让它训练。
- 强化学习:根据每次的结果给计算机一个反馈(分数),让它根据反馈自动优化。


强化学习eg:机器人走路,只有一个通道,让它自己选择路径,当走到好的路径时给它+3分,走到坏的路径-3分。它就会自动寻找能获得高分的路径。
各类学习的应用场景

2.线性回归
2.1什么是回归分析?
? 对于初学者,直接讲线性回归可能会让初学者懵逼,我是谁?我在哪?我在干什么?这玩意有啥用?因此,有必要从从基本的概念入手,到底什么是回归分析?(Regression Analysis)
? 如图,下面的三个案例给出了三个问题,这三个问题都是预测问题,那我们如何去做呢?当然是去找很多样本画图找规律喽。拿第一个问题举例,根据图上样本的分布规律,我们很容易发现它是一条斜率逐渐减小的递增曲线,从而根据曲线完成预测。但是如何让计算机看懂这个图?同样地,让它找到一条合适的曲线来拟合图上的样本点。这个拟合过程就叫回归,另外两个案例同理。

? 举过例子了,下面抛出概念可能会比较容易理解了。

可以说,回归分析就是根据去拟合一条曲线,而拟合一条合适的曲线的方法就是确定该曲线对应的合适的参数。比如数据点趋于一条直线,我们就是要找到一条合适的直线y=ax+b,而确定合不合适关键就在于a和b这两个参数,因此不断调参找到合适的直线就是回归分析做的事。至于回归的种类,理解一种即可,其他原理类似。
2.2线性回归
在了解什么是回归分析后,线性回归简直太好理解了。简单来说,它就是由数据拟合一条直线的回归分析。

最后,回归问题属于机器学习中的监督学习(你告诉计算机哪些是对的样本,哪些是错的,再让它训练)
2.3回归问题求解
至此,我们已经了解了什么是线性回归,那回归问题如何求解呢?先来看一个问题

左边是问题,右边是解决方案。我们知道回归问题就是画图,根据样本点拟合一条曲线,这条曲线就是定量关系P=f(A),在得到函数之后,这个问题就是小学初中的问题了,不再赘述。
? 显然,回归问题的重点和难点是求定量关系,那如何去求?啥都别问先把图搞出来。

根据图,我们发现可以用很多曲线来拟合数据,但是这里为了简单,先从最基本的线性模型y=ax+b开始拟合,用其他曲线拟合的思想是一样的。找到合适的线性模型y=ax+b的关键是参数a和b,可以先直观地体会一下a和b对线性模型的影响。

为了找到合适的a和b,我们可以考虑从结果反推,什么样的模型是好的?当然是线离大多数点近啊!那更准确点呢?这个大牛已经研究好了,就是对于每一个样本点,算一下它与线当前纵坐标的差值的平方,再把所有的样本点所求的结果求和,取这个和的最小值,也就是右下角的公式。为了后续方便,可以在对这个结果除以2m,也就得到了我们常听的损失函数,把这个损失函数记为J。

其实除不除以2m对最后的结果都没有影响,只是为了方便后面求导计算约掉2m。
那原问题就转换成了找一个a和b,使得损失函数的值最小。
为了直观的看一下损失函数的意义和效果,可以做一个小图,放几个样本点,用两条不同的直线拟合它,观察损失函数的值以及对应的拟合效果。

表格中的x和y列为实际样本点的横纵坐标,y1’和y2’为预测的纵坐标的值,也即是拟合曲线上的预测点。计算y1’和y2’对应的损失函数得J1和J2,如下图。

显然J1<J2,而在图像上y1’显然比y2’的拟合效果好。从这个案例就可以体会出损失函数的价值。
回到原来的问题,如何确定合适的a和b从而找到最小的损失函数J?在损失函数公式中,可以把yi’=axi+b-yi带入公式,得到J与a和b的关系g,可以令J=g(a,b)。等等,这怎么有点像多元函数求极值的问题,那能用高数中的多元函数求极值的方法来求解这个问题吗?我也不清楚,先留个疑问吧,等知识丰富了再回来想这个问题。在人工智能领域提出了大名鼎鼎梯度下降法很好地解决了这个问题,它可以自动地寻找极小值。

介绍一下梯度下降法。打个比方,它的效果类似于把一个钢珠放在在一个开口向上的槽的半坡,让它自己滚动,它会晃来晃去,最终停到极小值点。而具体的实现办法就是上图的公式,当前点的横坐标为pi,那么搜索的下一个点的位置为p(i+1),然后用上图公式就能得到下一个点的坐标了,然后把p(i+1)当做当前的点,再套用上面公式算出下一个点的坐标,直到它收敛即可得到极小值点的横坐标。公式怎么来的我也不知道,肯定是大牛搞出来的,目前我的水平也不需要理解,记住会用就行了。更多有关梯度下降的细节,可以参考网上的视频和博客。
2.4线性回归实战准备
首先认识一下sklearn,一个强有力的机器学习的开源框架。

其功能非常强大,常见的算法很快就能写出来。
eg:调用sklearn求解线性回归问题?
分析: 通过上一小节,我们已经知道求解线性回归最重要的就是确定得y=ax+b中的a和b两个参数。sklearn中有相应的包,使用包里面的函数可以快速求得参数a和b。

- 导入LinearRegression包
- 新建一个LinearRegression实例lr_model
- 调用fit方法拟合模型,就可以找出参数a和b了
- 使用拟合的模型对新数据进行预测
模型评估
模型评估的指标有很多,后续章节会专门介绍,但这个小实战先简单介绍一下这三个指标

- MSE和损失函数非常像,就差一个分母的2,它越小越好。
- R^2=1-(MSE)/方差,这个原理暂时不太懂,姑且先放一放,知道它是小于1且越接近1越好。
- 画图对比y与y’,将模型可视化来评估模型好坏,比较直观。
具体的实现方法如下:

在作图时,可能需要将多个图放在一起展示,使用subplot方法即可实现,比如subplot(211)的意思就是两行1列选择第一个行。

2.5单因子线性回归实战
2.5.1准备工作
本次实战会用到如下两个csv文件

generated_data.csv文件是自己造的一个简单数据,主要用于学习起来简单方便,内容如下。

usa_housing_price.csv文件时美国一些房价及影响因素的数据,内容如下。

打开anaconda,切换到你创建学习本项目的环境,打开notebook,在对应文件夹下创建文件lr_generated_data.ipynb保存

2.5.2回顾与步骤梳理
任务:
基于generated_data.csv数据,建立线性回归模型,预测x=3.5对应的y值,评估模型表现
在前面的线性回归章节已经介绍过如何建立线性回归模型了,再温习一下步骤。
- 加载数据
- 取出数据
- 观察数据
- 使用skleran建立线性回归模型
- 使用建立的模型进行预测
- 得出线性模型y=ax+b的两个重点参数a和b
- 评价模型:MSE(均方差)、r2分数、画预测值与实际值的图看他是否逼近y=x
下面将围绕这几个步骤进行展开。
2.5.3加载数据
#加载数据
import pandas as pd
lr_data = pd.read_csv("generated_data.csv")#使用read_csv函数,非常常用,务必记住!!
lr_data.head()#显示前5行数据

pandas基本操作忘了的话,建议回第一章第7节看看,至于函数的使用,多记多百度,前期啥都不知道肯定是要记一些最常用的。
2.5.4取出数据
#取出x和y列数据
x = lr_data.loc[:,'x']
y = lr_data.loc[:,'y']
print(type(x))
print(x)
print(type(y))
print(y)

一样,loc用法也在第一章第7节,忘了回去看。一般取出数据之后,都查看一下,如果数据多的话就用head看前5行。
2.5.5观察数据
#画一下点看看数据长什么样子
from matplotlib import pyplot as plt
plt.figure()
#画直线或散点图均可
plt.scatter(x,y)
#plt.plot(x,y)
plt.show()

由于是自己造出来的完美数据,这些点正好是直线上的点。
2.5.6使用skleran建立线性回归模型
#使用sklearn建立线性回归模型
from sklearn import linear_model
lr_model = linear_model.LinearRegression()
#查看当前x、y及维度:1维
print(type(x),x.shape)
print(type(y),y.shape)

用到了sklearn下的linear_model,然后创建一个对象,后面会用对象调用函数。官方文档下都有用法,还是要过看官方文档,csdn,多百度,多记。
此处应注意x和y都是1维的,也就是向量形式。
import numpy as np
#直接使用fit会失败,因为它要求传入的x参数为二维数组,因此要将一维的x转换成二维的
x = np.array(x)
x = x.reshape(-1,1)
y = np.array(y)
y = y.reshape(-1,1)
#再次查看当前x、y及维度:2维
print(type(x),x.shape)
print(x)
print(type(y),y.shape)
print(y)

此处要将x转换成2维的,也就是转换成矩阵形式,其实y可以不用转换(这里目前还是有点小疑问,不过根据后面的实操得出的结论是这样)。另外关于reshape的用法参考 https://blog.csdn.net/u010916338/article/details/84066369 和 https://www.zhihu.com/question/52684594 。
#使用fit构建线性回归模型
lr_model.fit(x,y)

构建模型很简单,就这一个fit函数,传入x和y的坐标集,它自己就能拟合得到一个线性模型。
2.5.7使用建立的模型进行预测
#使用构建的模型预测x对应的y(应该为完美预测)
y_predict = lr_model.predict(x)
print(y_predict)

传入原始数据中的x去进行预测,由于这个数据是完美数据,模型也是完美的,因此得到的预测值肯定也是完美的(即预测点就在直线上)。但在平时处理中,数据不是完美的,所以主要是看评价模型的指标,大多数情况直接看预测结果是没意义的。
#使用构建的模型预测x=3.5时y的值
y_predict2 = lr_model.predict([[3.5]])
print(y_predict2)

当然这个也是完美预测。。。
2.5.8得出线性模型y=ax+b的两个重点参数a和b
#根据模型得出参数a和b并显示出来
a = lr_model.coef_
b = lr_model.intercept_
print(a,b)

使用这 coef_ 和 intercept_ 即可得到参数a和b,那这得到的对不对呢?看看原始数据。
选中所有的x和y(不包括这两个字母)点插入中的散点图。

右键其中一个散点,选择趋势线。

在下面勾选显示公式,可以看到公式为y=2x+5,而上面的参数a、b就是2和5,这就证明上面求得的参数是正确的。


2.5.9评价模型
评价指标的3个常用方式MSE、r2分数、画y和y_predict的图,都记住吧。
from sklearn.metrics import r2_score,mean_squared_error
#评价指标:均方差MSE和R2分数
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print(MSE,R2)

#评价指标:画图
plt.figure()
plt.plot(y,y_predict)
plt.show()


2.6多因子线性回归实战
线性回归预测房价
任务: 基于usa_housing_price.csv数据,建立线性回归模型,预测合理房价:
1、以面积为输入变量,建立单因子模型,评估模型表现,可视化线性回归预测结果
2、以income、house age、numbers of rooms、population、area为输入变量,建立多因子模型,评估模型表现
3、预测Income=65000, House Age=5, Number of Rooms=5, Population=30000,size=200的合理房价 X_test = [65000,5,5,30000,200]
与单因子线性回归类似,只是输入换成了多因子,步骤如下:
- 导入数据
- 展示数据
- 以面积为输入变量建立单因子模型
- 使用sklearn构建线性模型
- 使用模型预测房价
- 评估模型
- 画图评估
- 建立多因子模型
- 拟合线性模型
- 预测新数据
- 评估模型
- 画图评估
- 预测Income=65000, House Age=5, Number of Rooms=5, Population=30000,size=200的合理房价 X_test = [65000,5,5,30000,200]
2.6.1导入数据
#导入数据
import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
data = pd.read_csv("usa_housing_price.csv")
data.head()

2.6.2展示数据
#展示一下数据
fig = plt.figure(figsize=(15,7))
fig1 = plt.subplot(231)
plt.scatter(data.loc[:,'Avg. Area Income'],data.loc[:,'Price'])
plt.title('Income VS Price')
fig2 = plt.subplot(232)
plt.scatter(data.loc[:,'Avg. Area House Age'],data.loc[:,'Price'])
plt.title('Age VS Price')
fig3 = plt.subplot(233)
plt.scatter(data.loc[:,'Avg. Area Number of Rooms'],data.loc[:,'Price'])
plt.title('Number VS Price')
fig4 = plt.subplot(234)
plt.scatter(data.loc[:,'Area Population'],data.loc[:,'Price'])
plt.title('Population VS Price')
fig5 = plt.subplot(235)
plt.scatter(data.loc[:,'size'],data.loc[:,'Price'])
plt.title('size VS Price')
plt.show()

2.6.3以面积为输入变量建立单因子模型
#以面积为输入变量建立单因子模型
#获取X和y
X = data.loc[:,'size']
y = data.loc[:,'Price']
X = np.array(X).reshape(-1,1)
2.6.4使用sklearn构建线性模型
#使用sklearn构建线性模型
from sklearn import linear_model as lm
lr1 = lm.LinearRegression()
lr1.fit(X,y)
2.6.5使用模型预测房价
#使用模型预测房价
y_predict1 = lr1.predict(X)
print(y_predict1)

2.6.6评估模型
#评估模型
from sklearn.metrics import mean_squared_error,r2_score
MSE1 = mean_squared_error(y,y_predict1)
R2_score1 = r2_score(y,y_predict1)
print(MSE1,R2_score1)

2.6.7画图评估
#画图评估
fig6 = plt.figure(figsize=(5,5))
plt.scatter(X,y)
plt.plot(X,y_predict1,'g')
plt.show()

2.6.8建立多因子模型
#建立多因子模型
#定义X_muti和y
X_muti = data.drop('Price',axis=1)
y = data.loc[:,'Price']
X_muti.head()
#y.head()

2.6.9拟合线性模型
#拟合线性模型
from sklearn import linear_model as lm
lr_muti = lm.LinearRegression()
lr_muti.fit(X_muti,y)
2.6.10预测新数据
#预测新数据
lr_muti_predict = lr_muti.predict(X_muti)
print(lr_muti_predict)

2.6.11评估模型
#评估模型
from sklearn.metrics import r2_score,mean_squared_error
lr_muti_r2_score = r2_score(y,lr_muti_predict)
lr_muti_mse = mean_squared_error(y,lr_muti_predict)
print(lr_muti_mse,lr_muti_r2_score)

#与之前的单因子模型相比,r2分数好的多(比单子更接近1),mse小了10倍,显然该案例多因子模型更好一点
print(MSE1,R2_score1)

2.6.12画图评估
#画图评估模型
from matplotlib import pyplot as plt
fig7 = plt.figure(figsize=(8,5))
plt.scatter(y,lr_muti_predict)
plt.title("Price VS Price_predict under multiple factors")
plt.show()#从图上看,预测值和实际值的重合部分比较多,效果不错

#与单因子的对比一下
fig8 = plt.figure(figsize=(8,5))
plt.scatter(y,y_predict1)
plt.title("Price VS Price_predict under single factors")
plt.show()#oh my god 效果简直好太多了!

2.6.13预测给定参数下的合理房价
#预测Income=65000, House Age=5, Number of Rooms=5, Population=30000,size=200的合理房价 X_test = [65000,5,5,30000,200]
import numpy as np
X_muti2 = [65000,5,5,30000,200]
#将向量转为二维矩阵以便能作为参数传入predict函数
X_muti2 = np.array(X_muti2).reshape(1,-1)
print(X_muti2)

lr_muti_predict2 = lr_muti.predict(X_muti2)
print(lr_muti_predict2)


第三章 机器学习之逻辑回归
1.分类问题介绍
线性回归主要是解决一个回归问题的,而逻辑回归则是解决分类问题的。至于为什么逻辑回归有“逻辑”二字但却是解决分类问题的,我的理解是分类也是一种特殊的回归。有兴趣自行百度。
来看下分类问题的实例:




定义

分类的方法

分类任务与回归任务的明显区别

2.逻辑回归讲解
2.1分类任务
我们现在已经知道了逻辑回归是处理分类任务的,那什么是分类也很容易理解,有如下案例

如何让机器理解这个任务呢?这就要先看一下分类任务的框架是怎样的。
分为两步,第一步是先求解一个最终的结果,就是下图中的y=f(x1,x2,xn),第二步就是根据该结果来判别类别。

? 在这个看电影案例中,第一步就是y=f(x)∈{0,1} (0表示不看电影,1表示看电影),第二步就是根据f(x)的值判断类别。显然,关键在于找出f(x)。
? 为了找出f(x),可以先使用简单地线性模型看一下点的分布情况,如下图。

可以得出分布函数y=0.1364x+0.5,那基于这个分布函数很容易就能得出看电影的情况,当y>=0.5时,去看电影,否则不去。
来看一下在此情况下的预测准确率,貌似非常不错。

但其实它有很大的局限性,它不够灵活,当样本量变大以后,准确率可能会下降的很快。比如下面案例中由于一个样本点向右偏离了很多,导致线性回归函数整体偏移了很多,这显然很呆。这时逻辑回归就派上用场了。

2.2逻辑回归的分布函数
相比线性回归,逻辑回归主要的不同在于分布函数,逻辑回归的分布函数为 y=1/(1+e^(-x)) ,也叫sigmoid函数,分布函数如下。

定义

那将逻辑回归应用于看电影的案例就是如下答案

2.3多维度下的分类任务
当有高维个影响因素时,只需将sigmoid函数进行适当的替换即可。比如当影响结果的因素为二维(x1,x2)时,可以把sigmoid函数中的x替换成下图右侧的g(x),至于更高维度的,同样也是替换,只是g(x)也会更高维。

而这个g(x)就被称为决策边界,我们解决分类任务最重要的就是找到它。
同样地,找到下面这个决策边界也就是找到g(x),当g(x)中包含二次项时,也意味着他是曲线,灵活度更高,可以看出它在下面的分类问题中作用非常好。

3.逻辑回归求解

这里sigmoid函数是固定的,关键是求解g(x),也就是决策边界。而得到g(x)的关键又是得到它的参数,在后面的实战中会使用sklearn得到这几个参数。
对于逻辑回归,它的损失函数不同于线性回归的,因为它的点是离散型的,因此使用下面的损失函数。感兴趣的可以百度查查相关知识。

逻辑回归的损失函数可以合并为一个式子,如下图。有了损失函数的式子,最后求解逻辑回归的问题就转化成了求最小的损失函数了,使用梯度下降法即可。

4.实战准备
? 使用matplotlib画分类点时,要使用mask进行标记,当mask为true时是一个类别,为false又是一个不同的类别,然后在画点的时候把不同类别的点后用mask标记一下即可。

使用逻辑回归实现二分类与线性回归那块类似

下面还要了解一下得到参数theta0、theta1、theta2(一阶线性)的过程,这就是决策边界的那三个参数。如果决策边界为曲线时,那应该引入平方项,并重新构建一个字典。

模型评估方面引入准确率,比较简单。

准确率实现方法及边界曲线可视化如下

5.考试实战
**任务: ** 逻辑回归预测考试通过。
基于examdata.csv数据,建立逻辑回归模型 预测Exam1 = 75, Exam2 = 60时,该同学是 passed or failed; 建立二阶边界,提高模型准确度
导入csv文件
#read the data
import pandas as pd
import numpy as np
data = pd.read_csv('examdata.csv')
data.head()

得到X和y
此处X为2维,有两门考试嘛。y是一维,表示通过与否。
#get X and y
X = data.drop('Pass',axis=1)
y = data.loc[:,'Pass']
X1 = data.loc[:,'Exam1']
X2 = data.loc[:,'Exam2']
X2.head()

可视化数据
#visualize the data
from matplotlib import pyplot as plt
fig1 = plt.figure(figsize=(8,5))
plt.title('Exam1 VS Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
plt.scatter(X1,X2)
plt.show()

分类后的可视化
#visualize the data
from matplotlib import pyplot as plt
fig2 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('Exam1 VS Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
plt.legend([passed,failed],['pass','fail'])
plt.show()

模型构建与预测
#establish the model and fit
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(X,y)
predict1 = lr.predict(X)
print(predict1)

用准确率评估模型
#evaluate the model
from sklearn.metrics import accuracy_score
accuracy_score(y,predict1)

预测特定数据下的通过情况
#预测Exam1 = 75, Exam2 = 60时,该同学是 passed or failed
predict2 = lr.predict([[75,60]])
print('passed' if predict2==1 else 'failed')

得到决策边界的参数
#得到决策边界函数
theta0 = lr.intercept_
theta1 = lr.coef_[0][0]
theta2 = lr.coef_[0][1]
X2_new = -(theta0+theta1*X1)/theta2
可视化决策边界
#visualize the boundary
fig3 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('Exam1 VS Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
boundary = plt.plot(X1,X2_new,c='r')
plt.legend([passed,failed],['pass','fail'])
plt.show()


建立2阶边界,也就是曲线
#建立二阶边界,提高模型准确度
#get the new data
X1_2 = X1*X1
X2_2 = X2*X2
X1_X2 = X1*X2
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)
print(X_new)

构建模型并预测
lr2 = LogisticRegression()
lr2.fit(X_new,y)
predict3 = lr2.predict(X_new)
print(predict3)

用准确率评估模型
#get the accuary_score
accuracy_score(y,predict3)

对x1进行排序,使得可视化地时候决策边界是一条平滑的线
X1_new = X1.sort_values()
print(X1,X1_new)

得到二阶决策边界的参数,并通过决策边界=0的方程计算出X2的坐标
#get the new X2 inorder to draw the boundary easily
theta0 = lr2.intercept_
theta1,theta2,theta3,theta4,theta5 = lr2.coef_[0][0],lr2.coef_[0][1],lr2.coef_[0][2],lr2.coef_[0][3],lr2.coef_[0][4]
a = theta4
b = theta2+theta5*X1_new
c = theta0+theta1*X1_new+theta3*X1_new*X1_new
#print(theta0,theta1,theta2,theta3,theta4,theta5)
X2_new2 = (-b+np.sqrt(b*b-4*a*c))/(2*a)
print(X2_new2)


可视化二阶决策边界
#draw the boundary
fig4 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('Exam1 VS Exam2')
plt.xlabel('Exam1')
plt.ylabel('Exam2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
boundary2 = plt.plot(X1_new,X2_new2,c='r')
plt.legend([passed,failed],['pass','fail'])
plt.show()

6.芯片监测实战
任务: 逻辑回归预测芯片质量通过
1、基于chip_test.csv数据,建立逻辑回归模型(二阶边界),评估模型表现;
2、以函数的方式求解边界曲线
3、描绘出完整的决策边界曲线

步骤如下:
(1)加载数据
(2)可视化数据
(3)定义X和y,得到对应参数及相关数据
(4)建立模型、训练、预测
(5)评估模型
(6)找到决策边界(二阶)
(7)自定义边界函数
加载数据
#read the data
import pandas as pd
import numpy as np
data = pd.read_csv('chip_test.csv')
data.head()

获得X和y
#get X and y
X = data.drop('pass',axis=1)
y = data.loc[:,'pass']
X1 = data.loc[:,'test1']
X2 = data.loc[:,'test2']
X2.head()

可视化分类后的数据
#visualize the data
from matplotlib import pyplot as plt
fig2 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('test1 VS test2')
plt.xlabel('test1')
plt.ylabel('test2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
plt.legend([passed,failed],['pass','fail'])
plt.show()

直接建立二阶曲线边界
#建立二阶边界,提高模型准确度
#get the new data
X1_2 = X1*X1
X2_2 = X2*X2
X1_X2 = X1*X2
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}
X_new = pd.DataFrame(X_new)
print(X_new)

建立模型并预测
lr2 = LogisticRegression()
lr2.fit(X_new,y)
predict3 = lr2.predict(X_new)
print(predict3)

用准确率评估模型
#get the accuary_score
accuracy_score(y,predict3)
对x1排序以便画好边界曲线
X1_new = X1.sort_values()
print(X1_new)

获取决策边界的参数,并定义新增平方项和混合项的新字典
#get the new X2 inorder to draw the boundary easily
theta0 = lr2.intercept_
theta1,theta2,theta3,theta4,theta5 = lr2.coef_[0][0],lr2.coef_[0][1],lr2.coef_[0][2],lr2.coef_[0][3],lr2.coef_[0][4]
a = theta4
b = theta2+theta5*X1_new
c = theta0+theta1*X1_new+theta3*X1_new*X1_new
#print(theta0,theta1,theta2,theta3,theta4,theta5)
X2_new2 = (-b+np.sqrt(b*b-4*a*c))/(2*a)
print(X2_new2)

画出决策边界
#draw the boundary
fig4 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('test1 VS test2')
plt.xlabel('test1')
plt.ylabel('test2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
boundary2 = plt.plot(X1_new,X2_new2,c='r')
plt.legend([passed,failed],['pass','fail'])
plt.show()

由于求解x2的时候,只用了一个求根公式 x=(-b+sqrt(b*b-4ac))/(2*a) ,因此决策边界只有一条,想画全就同时得到求根公式的两个x即可,于是就有下面的自定义边界函数f(x)。
自定义边界函数
#自定义边界函数f(x)
def f(x):
a = theta4
b = theta2+theta5*x
c = theta0+theta1*x+theta3*x*x
boundary1 = (-b+np.sqrt(b*b-4*a*c))/(2*a)
boundary2 = (-b-np.sqrt(b*b-4*a*c))/(2*a)
return boundary1,boundary2
获得两条边界曲线的纵坐标
#获得两条边界函数test1对应的test2
line1 = []
line2 = []
for x in X1_new:
line1.append(f(x)[0])
line2.append(f(x)[1])
print(line1,line2)

画出决策边界
#draw the boundary
fig5 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('test1 VS test2')
plt.xlabel('test1')
plt.ylabel('test2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
boundary3 = plt.plot(X1_new,line1,c='r')
boundary4 = plt.plot(X1_new,line2,c='r')
plt.legend([passed,failed],['pass','fail'])
plt.show()
#线并不闭合,是因为test1的样本点太少了,可以自己制造密集一点的点来补全

此时我们发现决策曲线还是不闭合,原因是数据点不够多,那我们只需要多生成一些点再画图即可。
生成密集的点以补全决策边界曲线
X1_customize = [-0.9 + i/20000 for i in range(0,38001)]#可以参考列表解析的用法
X1_customize = np.array(X1_customize)
#获得两条边界函数test1对应的test2
line3 = []
line4 = []
for x in X1_customize:
line3.append(f(x)[0])
line4.append(f(x)[1])
print(line3,line4)

画出决策边界
#draw the boundary
fig6 = plt.figure(figsize=(8,5))
mask=y==1
plt.title('test1 VS test2')
plt.xlabel('test1')
plt.ylabel('test2')
passed = plt.scatter(X1[mask],X2[mask])
failed = plt.scatter(X1[~mask],X2[~mask],marker='^')
boundary5 = plt.plot(X1_customize,line3,c='r')
boundary6 = plt.plot(X1_customize,line4,c='r')
plt.legend([passed,failed],['pass','fail'])
plt.show()
#线已经闭合了

大工告成!终于结束了,这章学完收货颇丰~
有很多一开始没接触过的东西都自己去百度了,真的学会了很多。
第四章 机器学习之聚类
1.无监督学习
无监督学习(Unsupervised Learning)
举个例子,下列有些猫的图片,对这些图片进行分类。再无监督学习的情况下,他会自动寻找这些图片的共同点,将相似的归为一类,并不需要你告诉他哪些图片是哪一类。

其定义、优点及应用如下:

无监督和监督学习的区别就是是否给数据打上label。
比如下图是监督学习,他会使用y来代表label的情况,根据x值给该数据打上相应的y(label)值。比如给红色的类打上0的label,给蓝色的类打上1的label,分别代表0和1类。

而无监督学习则没有label项,在划分为两个类后,这两个类谁是0类谁是1类都无所谓。

聚类分析
聚类分析又称为群分析,根据对象某些属性的相似度,将其自动划分为不同的类别。
常用的聚类算法



2.Kmeans-KNN-Meanshift
2.1什么是Kmeans
KMeans Analysis也叫K均值聚类

其实这个算法很简单,就是不断地更新聚类中心的位置,直到收敛。其算法的具体步骤如下:

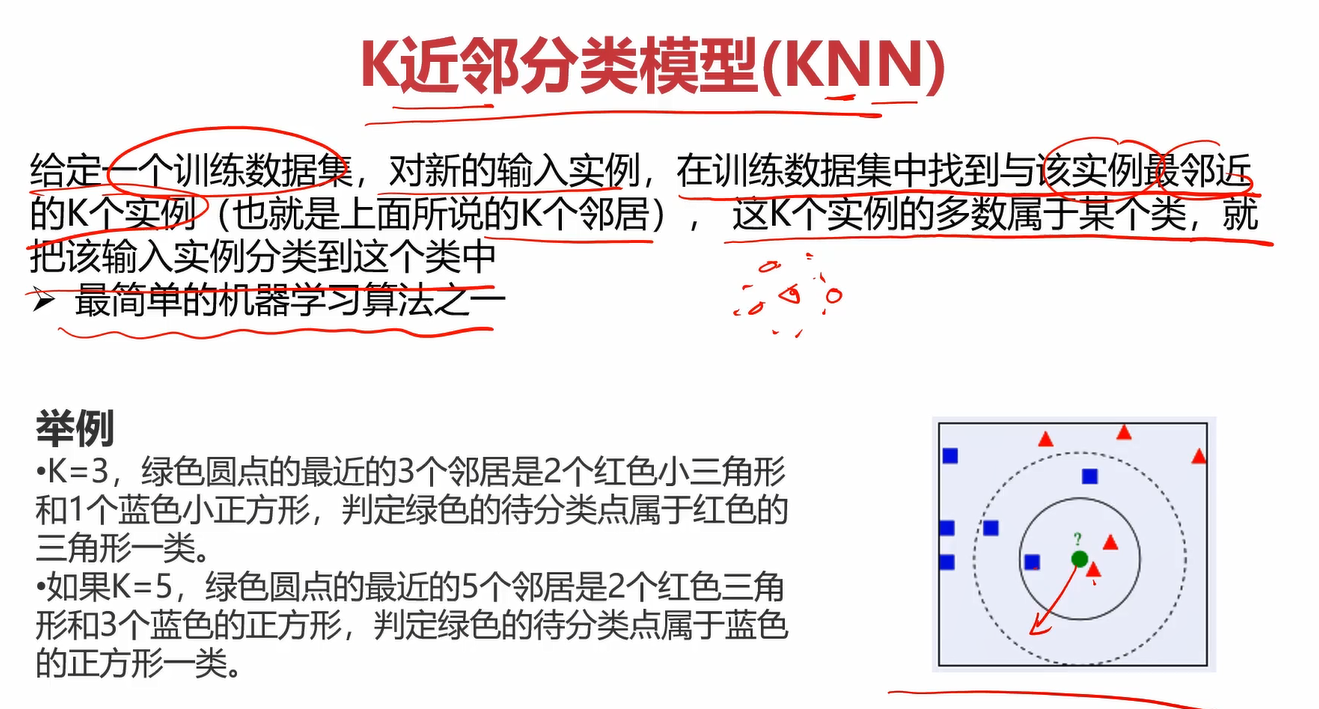
2.2什么是KNN
KNN也叫K近邻分类模型

2.3什么是Meanshift
Meanshift也叫均值漂移聚类

其算法流程为:

关于此处的每一个算法,我并没有过多的在笔记中记录。一方面是单纯使用文字很难讲解,看视频会比较好一点。另一方面是我的笔记是针对快速回忆以及重点知识的理解的,我觉得这些已经足够我回忆起来了,并且每个算法并不难理解。因此推荐第一次接触的兄弟们看看每个算法的讲解原理,再看上面几个图片就能通透很多。后面很多章节我也不会记得特别详细,毕竟这是笔记而不是讲课。
3.实战准备
3.1KMeans预备知识
在之前学习的基础上,这里模型的训练流程应该都能理解。
需要注意的就是定义KMeans对象时往里面传的参数: n_clusters=3 和 random_state=0。
n_clusters=3就是你要聚成几个类,=3说明要聚3个类。
关于random_state=0,参考了一些博客,得出如下结论:
如果你在需要设置random_state 的地方都设置好,那么当别人重新运行你的代码的时候就能得到完全一样的结果,复现和你一样的过程。如果你设置为None,则会随机选择一个种子。
那么让它=0也是为了固定种子的值,以便后续我们可以保证当前随机性的复现。

获取聚类中心点的方法为KM.cluster_centers_
准确率都会,就不说了,emmm,kmeans好像也没啥了。
哦,这里还有个要注意,由于kmeans是无监督学习,因此他没有label,分类完成是没啥问题,但分出来的类标签可能有问题,这时就需要用到校正。方法也很简单,可以画个图看看是哪几个标签打反了,使用列表校正即可,再将矫正后的数据转为numpy的array就得到正确的带标签分类结果了。

3.2Meanshift预备知识
这个挺简单地,带宽可以自动计算出来或者手动给定(一般都自动计算,因为你也不知道给多少合适)
estimate_bandwidth传入的参数X为数组,n_samples为使用的样本数,不指定,就使用所有的样本。
estimate_bandwidth(X,n_samples=500)的意思就是在X中以500个样本数据进行估算,得出合适的带宽。
最后构建模型需要传入带宽。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-OwJWBeuM-1630847148520)(C:\Users\doubleguy\AppData\Roaming\Typora\typora-user-images\image-20210831224737834.png)]
3.3KNN预备知识
KNN贼简单,定义个KNN分类器创建实例就完事~
唯一需要注意的就是训练的时候要传入y,因为他是监督学习,你需要传入对应的label。而KMeans和Meanshift是无监督学习,训练的时候就不需要label。

4.Kmeans实战
任务: 2D数据类别划分
1、采用Kmeans算法实现2D数据自动聚类,预测V1=80,V2=60数据类别;
2、计算预测准确率,完成结果矫正
3、采用KNN、Meanshift算法,重复步骤1-2
数据:data.csv
开工~
老样子,先new个新文件,名字如下(我已经弄好了)

读取数据
#读取数据
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
data = pd.read_csv('data.csv')
data.head()

定义X和y
# 定义X和y
X = data.drop('labels',axis=1)
y = data.loc[:,'labels']
y.head()

#看一下标签的分布情况(看看有多少类,每类有多少个样本)
pd.value_counts(y)

画出数据观察分布
#画出原始数据
fig1 = plt.figure(figsize=(8,6))
plt.scatter(data.loc[:,'V1'],data.loc[:,'V2'])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('unlabeled data')
plt.show()

#给原始数据打上标签
fig2 = plt.figure(figsize=(8,6))
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('labeled data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()

构建Kmeans模型
#创建Kmeans实例,使用kmeans训练模型
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3,random_state=0)
kmeans.fit(X,y)

得到簇中心
#得到簇中心
cluster_center = kmeans.cluster_centers_
print(cluster_center)

#可视化簇中心(红色点为簇中心)
fig3 = plt.figure(figsize=(8,6))
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('labeled data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.scatter(cluster_center[:,0],cluster_center[:,1])#切片操作:[行切片操作,列切片操作]
plt.show()

进行预测
#对v1=80,v2=60的数据进行分类预测
y_predict1 = kmeans.predict([[80,60]])
print('label%d' % y_predict1)
#从图上看,它应该归为label2类,但预测结果竟然为label1类,显然是有问题的

#看看对原训练数据的预测效果如何
y_predict2 = kmeans.predict(X)
#对比一下预测结果和原数据的标签
print(pd.value_counts(y_predict2),pd.value_counts(y))

计算准确率
#计算预测准确率
from sklearn.metrics import accuracy_score
print(accuracy_score(y,y_predict2))

这个准确率低的吓人,说明哪里出错了,画个图瞧瞧
#画出当前预测结果与原数据图的对比
fig4 = plt.figure(figsize=(11,4))
plt.subplot(1,2,1)
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('original data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
fig5 = plt.subplot(1,2,2)
label0 = plt.scatter(data.loc[:,'V1'][y_predict2==0],data.loc[:,'V2'][y_predict2==0])
label1 = plt.scatter(data.loc[:,'V1'][y_predict2==1],data.loc[:,'V2'][y_predict2==1])
label2 = plt.scatter(data.loc[:,'V1'][y_predict2==2],data.loc[:,'V2'][y_predict2==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('predicted data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()
#发现虽然kmeans虽然帮我们分好类了,但是标签打错了,只需要重新调整一下标签即可

原来分类虽然基本正确了,但标签打错了,进行校正。
校正
#校正预测结果的标签
predict_correct = []
#自定义一个校正函数方便校正后预测某个指定数据的结果
def check(para,lis):
for x in para:
if x==0:
lis.append(1)
elif x==1:
lis.append(2)
else:
lis.append(0)
#校正完毕
check(y_predict2,predict_correct)
print(pd.value_counts(predict_correct),pd.value_counts(y))

predict_correct = np.array(predict_correct)
type(predict_correct)
画出矫正后的图像
#画出校正后的预测分类图
#画出当前预测结果与原数据图的对比
fig6 = plt.figure(figsize=(11,4))
plt.subplot(1,2,1)
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('original data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
fig7 = plt.subplot(1,2,2)
label0 = plt.scatter(data.loc[:,'V1'][predict_correct==0],data.loc[:,'V2'][predict_correct==0])
label1 = plt.scatter(data.loc[:,'V1'][predict_correct==1],data.loc[:,'V2'][predict_correct==1])
label2 = plt.scatter(data.loc[:,'V1'][predict_correct==2],data.loc[:,'V2'][predict_correct==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('kmeans predicted data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()

矫正后再计算准确率
#计算校正后的准确率
print(accuracy_score(y,predict_correct))

效果非常不错了~
此时再对v1=80,v2=60的数据进行分类预测
#校正后,再对v1=80,v2=60的数据进行分类预测
res = []
y_predict3 = kmeans.predict([[80,60]])
#已分类完毕,对标签进行校正
check(y_predict3,res)
print('label%d' % res[0])

KMeans实战就到这了~
5.KNN 实战
KNN是有监督学习,在构建模型时,需要传入相应的标签。
在以上代码的基础上,使用KNN算法构建模型。
构建KNN模型
#使用knn算法(有监督学习,训练时需要给出标签)
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=3)
knn.fit(X,y)

使用KNN模型进行预测
#使用knn建立的模型预测V1=80,V2=60对应的类别
knn_predict1 = knn.predict([[80,60]])
print(knn_predict1)

计算KNN模型预测准确率
#计算knn模型的准确率(准确率为1,表明模型效果很好)
from sklearn.metrics import accuracy_score
knn_predict2 = knn.predict(X)
print(accuracy_score(knn_predict2,y))

准确率竟高达100%!可见KNN模型的效果非常好。
观察一下数据的分布情况
#看看knn预测结果与原始给定结果的数据分布情况(发现完全一致,表明模型效果很好)
print(pd.value_counts(knn_predict2),pd.value_counts(y))

使用KNN得到的预测结果分类与原始数据的分类结果完全一致,说明KNN的效果非常好。
画出当前KNN模型
#画图看看knn模型的效果
#画出当前预测结果与原数据图的对比(完全一致,效果非常好)
fig8 = plt.figure(figsize=(11,4))
plt.subplot(1,2,1)
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('original data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
fig9 = plt.subplot(1,2,2)
label0 = plt.scatter(data.loc[:,'V1'][knn_predict2==0],data.loc[:,'V2'][knn_predict2==0])
label1 = plt.scatter(data.loc[:,'V1'][knn_predict2==1],data.loc[:,'V2'][knn_predict2==1])
label2 = plt.scatter(data.loc[:,'V1'][knn_predict2==2],data.loc[:,'V2'][knn_predict2==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('knn predicted data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()

如图,不仅图形的分布和原始数据一致,连标签也没有像Kmeans那样错乱,这样就不用再进行校正的步骤了。这是理所当然的,因为你的在创建KNN模型的时候就把对应的标签数据传进去了。
6.MeanShift实战
在前面的基础上,我们可以开始着手构建MeanShift模型了。
计算MeanShift模型要用的带宽
#使用meanshift算法(优先计算出带宽,也即球的半径)
from sklearn.cluster import estimate_bandwidth
bw = estimate_bandwidth(X,n_samples=500)
print(bw)

这里构建注意,在构建MeanShift模型的时候,要先给出他的带宽。可以自己给定带宽,也可以使用sklearn里面的方法自动估算带宽。一般来说我们不知道给多少合适,所以都是使用自动估算的方法。这里就是先把带宽自动计算出来,关于estimate_bandwidth方法,自己查阅把,应该不需要细说了~
构建MeanShift模型
#使用自动计算出的带宽构建模型
from sklearn.cluster import MeanShift
meanshift = MeanShift(bandwidth=bw)
meanshift.fit(X)#无监督不用传入标签

预测
#使用meanshift模型进行预测(结果不正确,说明构建模型有问题,可以看下结果标签与原始标签的分布对比情况)
meanshift_predict1 = meanshift.predict([[80,60]])
print(meanshift_predict1)

预测结果是0类,显然不对,V1=80,V2=60的数据点应该是2类。
观察数据分布
meanshift_predict2 = meanshift.predict(X)
print(pd.value_counts(y),pd.value_counts(meanshift_predict2))
#经过对比发现,meanshift模型的0类和2类标签正好打反了,解决方法同上面的kmeans校正

画图进一步观察错误
#可以画图看看错在哪了(由图得0类和2类标签反了)
#画出当前预测结果与原数据图的对比
fig8 = plt.figure(figsize=(11,4))
plt.subplot(1,2,1)
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('original data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
fig9 = plt.subplot(1,2,2)
label0 = plt.scatter(data.loc[:,'V1'][meanshift_predict2==0],data.loc[:,'V2'][meanshift_predict2==0])
label1 = plt.scatter(data.loc[:,'V1'][meanshift_predict2==1],data.loc[:,'V2'][meanshift_predict2==1])
label2 = plt.scatter(data.loc[:,'V1'][meanshift_predict2==2],data.loc[:,'V2'][meanshift_predict2==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('meanshift predicted data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()

由图可知,数据分类大致正确了,但是label打的不对,改正方法同KMeans,进行校正即可。
对label进行校正
#对meanshift预测的结果进行校正
meanshift_correct = []
for i in meanshift_predict2:
if i==0:
meanshift_correct.append(2)
elif i==1:
meanshift_correct.append(1)
else:
meanshift_correct.append(0)
meanshift_correct = np.array(meanshift_correct)
print(meanshift_correct)

查看校正后的数据分布
#校正后看下数据分布情况是否一致了(一致说明校正完成)
print(pd.value_counts(y),pd.value_counts(meanshift_correct))

由图发现,校正完数据分布已经恢复正常了。
画出校正后的数据图
#不放心的话就画图看看(完全一致,没有任何问题)
#画出当前预测结果与原数据图的对比
fig8 = plt.figure(figsize=(11,4))
plt.subplot(1,2,1)
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('original data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
fig9 = plt.subplot(1,2,2)
label0 = plt.scatter(data.loc[:,'V1'][meanshift_correct==0],data.loc[:,'V2'][meanshift_correct==0])
label1 = plt.scatter(data.loc[:,'V1'][meanshift_correct==1],data.loc[:,'V2'][meanshift_correct==1])
label2 = plt.scatter(data.loc[:,'V1'][meanshift_correct==2],data.loc[:,'V2'][meanshift_correct==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('meanshift predicted data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()

如图,显然校正成功,效果也是非常不错的~
准确率
最后看一下MeanShift的准确率
#看看meanshift的准确率(非常高了)
print(accuracy_score(meanshift_correct,y))
 rrect.append(2) elif i==1: meanshift_correct.append(1) else: meanshift_correct.append(0) meanshift_correct = np.array(meanshift_correct) print(meanshift_correct) ```
rrect.append(2) elif i==1: meanshift_correct.append(1) else: meanshift_correct.append(0) meanshift_correct = np.array(meanshift_correct) print(meanshift_correct) ```

查看校正后的数据分布
#校正后看下数据分布情况是否一致了(一致说明校正完成)
print(pd.value_counts(y),pd.value_counts(meanshift_correct))

由图发现,校正完数据分布已经恢复正常了。
画出校正后的数据图
#不放心的话就画图看看(完全一致,没有任何问题)
#画出当前预测结果与原数据图的对比
fig8 = plt.figure(figsize=(11,4))
plt.subplot(1,2,1)
label0 = plt.scatter(data.loc[:,'V1'][y==0],data.loc[:,'V2'][y==0])
label1 = plt.scatter(data.loc[:,'V1'][y==1],data.loc[:,'V2'][y==1])
label2 = plt.scatter(data.loc[:,'V1'][y==2],data.loc[:,'V2'][y==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('original data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
fig9 = plt.subplot(1,2,2)
label0 = plt.scatter(data.loc[:,'V1'][meanshift_correct==0],data.loc[:,'V2'][meanshift_correct==0])
label1 = plt.scatter(data.loc[:,'V1'][meanshift_correct==1],data.loc[:,'V2'][meanshift_correct==1])
label2 = plt.scatter(data.loc[:,'V1'][meanshift_correct==2],data.loc[:,'V2'][meanshift_correct==2])
plt.xlabel('V1')
plt.ylabel('V2')
plt.title('meanshift predicted data')
plt.legend([label0,label1,label2],['label0','label1','label2'])
plt.show()

如图,显然校正成功,效果也是非常不错的~
准确率
最后看一下MeanShift的准确率
#看看meanshift的准确率(非常高了)
print(accuracy_score(meanshift_correct,y))
