[人工智能]特征选择与降维

特征选择与降维可以说其本质目的是相同的，首要的一个目的就是为了应对维度灾难。随着以后所需处理的数据越来越大，可以直观的感受到样本的特征数呈现直线性的增长。特征选择与降维就是通过一定的算法来选择更为合适的、更具有代表性的的特征来替代原有的高维特征。总的来说，有这样的两个好处
1：极大避免维度灾难问题
2：往往能够去除一些不相关特征，针对我们的任务可以选择更为合适的特征。(特征选择)

特征选择

特征选择主流处理方法有三类，其中最为常用的是前两类处理方式
1：过滤式
2：嵌入式
3：包裹式

过滤式

过滤式首先是针对于数据的处理方法，相当于是先对数据进行处理然后再将处理后的数据送入模型进行训练。过滤式一般有以下两种方法。
1：方差选择法：低方差过滤
2：相关系数法

1：低方差过滤
低方差过滤的思想十分简单直观，首先要明确一点，机器学习中学习的是数据的分布情况，并非对数据的单个数值感兴趣。方差能够较好的衡量一组数据中数据的离散情况。低方差过滤就是将多个特征分布的方差较小删去，保留方差较大的特征。比如其中多维特征呈现【1，1，1，…，1】或者彼此之间方差的差距很小，那该多维特征对于机器来说就没有太大意义，保留一组，其余删去就可。

from sklearn.feature_selection import VarianceThreshold
from sklearn.datasets import load_wine

data = load_wine().data
print(data.shape) #原数据13维
transfer = VarianceThreshold(threshold=10)
data = transfer.fit_transform(feature)
# 输出特征选择后的数据维度信息
data.shape

2：相关系数法
其实仔细看上述的输出结果可知，假设1,2,3列方差很接近，呈现一致性的分布情况。但我们不能去人为的控制去除哪两行，只能由算法来决定。相关系数法则赋予了我们自主选择去除哪行的权力。通过计算两列之间的相关系数根据相关系数的大小进而来选择留下或者删除哪些数据信息。
2-1：皮尔逊相关系数

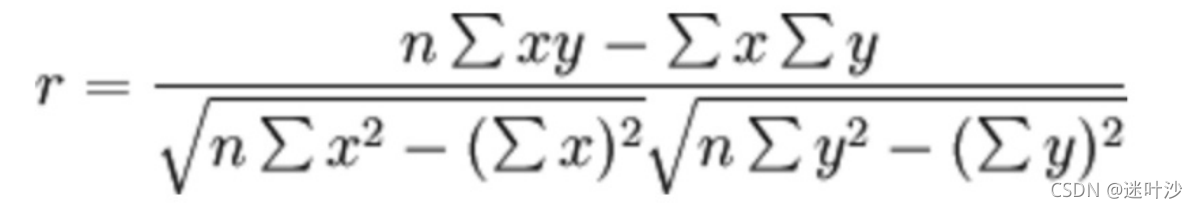
其中n代表样本数，x,y分别代表该数据集的两组特征

from scipy.stats import pearsonr

# 计算前两列特征的相关系数
# pearsonr返回一个元组，第一个数据代表两列特征之间的相关系数，第二个数粗略的表示了不相关系统产生具有皮尔逊相关性数据集的概率(不需要考虑)
score = pearsonr(feature[0],feature[4])

相关系数因子处于【-1，+1】之间，一般我们将|score[0]|<0.4称之为低度相关，0.4≤|score[0]|<0.7称之为显著性相关，
0.7≤|score[0]称之为高度线性相关

2-2：斯皮尔曼相关系数

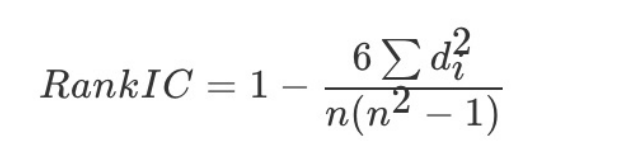
其中n代表等级个数，di代表等级差。举一个栗子
编号			身高		身高排序		年龄		年龄排序		排序等级差
1			190			1		23			3			2
2			170			3		24			4			1
3			155			4		30			5			1
4			180			2		19			1			1
5			152			5		20			2			3
排列等级差：两列特征排序差的绝对值

from scipy.stats import spearmanr
# 计算两列特征之间的斯皮尔曼系数
# 返回同皮尔逊系数基本一致，只需要关乎返回元祖的第一个数值，代表着二者之间的一个相关系数，取值在【-1,1】之间
score = spearmanr(feature[0],feature[1])

嵌入式

嵌入式顾名思义，嵌入吗。就是将特征选择过程与学习训练过程融为一体。其实在前面的经典机器学习算法中我们已经接触到了好几种嵌入式特征选择的方法。如：
1：决策树：根据信息增益，基尼指数等进行特征选择
2：正则化：L1正则化
3：深度学习中的卷积操作，也是有针对性的选择某些局部特征
正则化与L1，L2正则(点我，点我！！！)

包裹式

包裹式最大的特点是依据最终模型的学习性能作为准则来确定特征集的筛选，相当于是为该模型量身打造的数据特征。(量身打造往往就会造成模型的泛华性能可能较差，比较适合专任务专用的情景)经典的有LVW特征选择方法。这种方法在我们日常的使用中并不常见，因此感兴趣的去搜索下了解即可。

降维

降维是直接通过一定的算法来筛选原始特征，进一步的压缩特征空间，减少维度，避免维度灾难和没有意义的庞大重复性质的计算。主流方法有以下两种：
1：LDA
2：PCA（kernel PCA）

1-1：LDA（Linear Discriminant Analysis）

LDA本质上是一种给予监督学习的降维、分类算法。侧重于分类，因为每个数据带有标签。就是将高维空间上的点投影到低维空间上，通过已有的标签，根据算法选定不同的投影方向，最终找到一种更适合分类的空间。

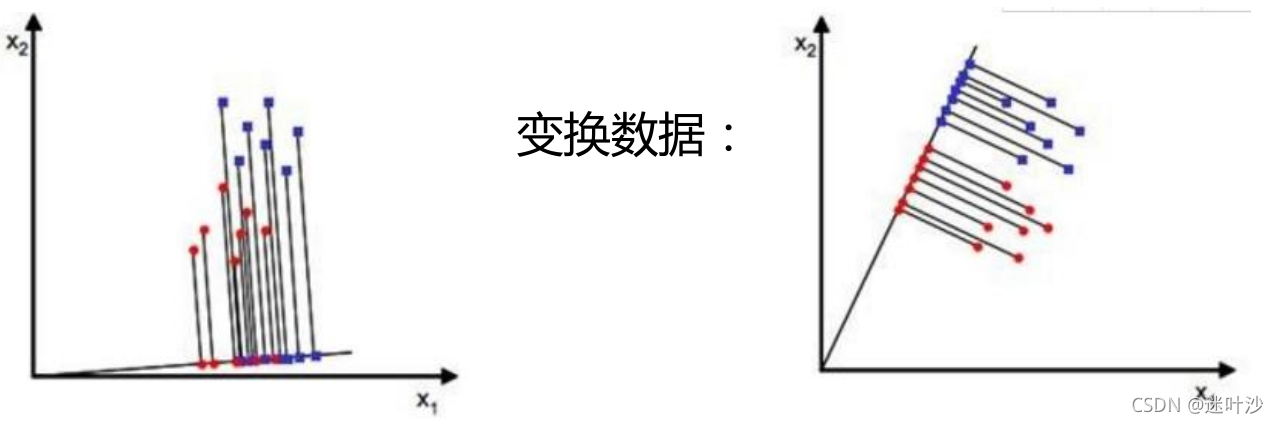
如上图所示，在二维空间中。为了达到我们所需的降维结果，我们可以做最简单的投影，将这些二维的点投影到一条直线上，
如上图左右两幅图所示，根据投影方向的不同，最终我们产生的降维后类别分类效果也有很大的差异，上右很明显
呈现了完美的分类效果。而上左投影后的效果仿佛更差，所以数据点集中在一起，更加难以区分。因此，lda其实就是
在帮助我们如何确定 y=Wx这样一个超平面，尽可能完美的实现我们降维后区分度增强的目标。
LDA算法目标：类内距离越近越好，类间距离远越越好

每维特征均值$u_i=\frac{1}{n}{\sum }_{x\in w_i}x$

投影之后的均值$u_i^{‘}=\frac{1}{n}{\sum }_{y\in w_i}y=\frac{1}{n}{\sum }_{x\in w_i}{w}^{T}x=w^T{u}_i$

总体均值$u=\frac{1}{n}{\sum }_{i\in n}{x}_i$

类间距离$dis0={\sum }_{i=1}^k|u_i^{‘}?u{|}^2,k:$类别数

from sklearn.datasets import load_wine

dataset = load_wine()
feature = dataset.data
target = dataset.target

# 计算每类的每个特征的均值
meanvalues = list()
for i in range(len(np.unique(target))):
    meanvalues.append(np.mean(feature[target==i],axis=0))
# 计算类间散射矩阵Sb
# 计算样本总体平均值
overall = np.mean(feature,axis=0).reshape(13,-1)
Sb = np.zeros((13,13))
for i,j in enumerate(meanvalues,1):
    mean = j.reshape(13,-1)
    # 获取类别中总的样本数
    n = feature[target==i,:].shape[0]
    # 类间距离由每个类内中间点与整体数据均值差来度量
    Sb+=n*(mean-overall).dot((mean-overall).T)

类内距离：每个数据减去均值的平方$s_i^2={\sum }_{y\in w_i}(y?u_i^{‘}{)}^2={\sum }_{x\in w_i}(w^{T}x?w^T{u}_i{)}^2={\sum }_{x\in w_i}{w}^T(x?u_i)(x?u_i{)}^{T}w$

我们将${\sum }_{x\in w_i}(x?u_i)(x?u_i{)}^T$称之为散列矩阵

总的类内距离$dis={\sum }_{i=1}^k{\sum }_{x\in w_i}{w}^T(x?u_i)(x?u_i{)}^{T}w$

令$Sw=所有散列矩阵之和$

$dis1=w^{T}Sww$

# 计算类内散射矩阵Sw
Sw = np.zeros((13,13))
for i,j in enumerate(meanvalues,1):
    mean = j.reshape(13,-1)
    class_inner = np.zeros((13,13))
    for k in feature[target==i,:]:
        sample_value = k.reshape(13,-1)
        class_inner += (sample_value-mean).dot((sample_value-mean).T)
    Sw += class_inner

目标函数$J(w)=\frac{w^{T}Sbw}{w^{T}Sww}$
是一个无约束性的问题，可以采用拉格朗日乘子法或者直接求导，本质都是一样的
化简后$S{w}^{?1}Sbw=\lambda w$,所以w就是$S{w}^{?1}Sb$矩阵对应的特征向量所构成的矩阵

eigenvalues,eigenvectors = np.linalg.eig(np.linalg.inv(Sw).dot(Sb))

# 获取eigen列表
eigen = [(np.abs(i),j) for i,j in zip(eigenvalues,eigenvectors)]
# 根据特征值进行排序，方便选取前d个最大的特征向量
eigen.sort(key=lambda x:x[0],reverse=True)

# 保留两维特征,特征值为复数形式我们保留实部
w = np.hstack((eigen[0][1][:,np.newaxis].real,
              eigen[1][1][:,np.newaxis].real))
x_lda  = feature.dot(w)

或者直接采取sklearn封装好的LDA算法

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

lda = LDA(n_components=2)
x_lda = lda.fit_transform(feature,target)
colors = ['r', 'b', 'g']
markers = ['+', 'x', 'o']

colors = ['r', 'orange', 'y']
markers = ['+', 'x', 'o']

for l, c, m in zip(np.unique(target), colors, markers):
    plt.scatter(x_lda[target == l, 0],
                x_lda[target == l, 1] ,
                c=c, label=l, marker=m)

plt.legend(loc='lower right')
plt.show()

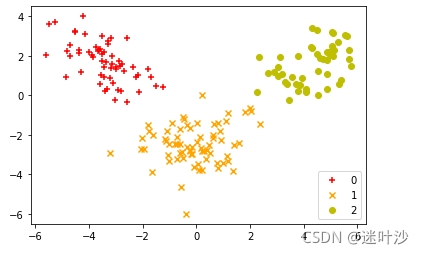
2-1:PCA（Principal Component Analysis）

PCA即我们常见的主成分分析方法，关注于数据之间的方差问题，最终使用样本间协方差来进行衡量。首先先简单说一下什么是主成分
主成分需要满足以下三个条件：
假设数据集$D=(x_1,x_2,...,x_n)$,其均值为$u$
定义一种映射变换$y_i={\alpha }_i^{T}x={\alpha }_{1i}{x}_1+{\alpha }_{2i}{x}_2+...+{\alpha }_{ni}{x}_n$
到这里学过矩阵论或者线代的应该明白了，这其实没有任何新的知识，就是一个矩阵的基变换，记得矩阵论上应该定义的是$y=Cx$,C就是基变化矩阵，这里一致。
条件1：系数向量${\alpha }_i^T$是单位向量，点积为1
条件2：映射后变量$y_i$两两之间相互正交，互不相关，也就是协方差$cov(y_i,y_j)=0$
条件3：$y_1$是所有映射变量中关于x线性变化方差最大的，$y_2$是与$y_1$（也就是与$y_1$正交）不相关x的线性变换方差最大的，其余的依次类推。(还是线代，矩阵论的老知识，有点最大线性无关向量组的味道)
这样我们称$y_i$为第i主成分

知道了主成分的概念，再加上我们目标是降维，换句话说就要要构造一种映射关系，使得可以使高维数据转变为低维数据。还是一个$y=wx$的问题，如何确定一组基，使得可以将高维数据转化为地位数据上。在LDA中通过类间、类内距离的度量来确定投影方向，那么PCA中如何来选定这样的一组方向也就是一组基呢？PCA中最直观的想法就是希望投影后的投影值尽可能的分散，也就是方差要大。为啥方差要大呢？方差大代表信息的分类越不相同，包含样本分布更多信息。

至此，先捋一捋要满足的条件。首先满足最开始三条要求，两两之间协方差为0，然后核心还要有方差来度量性能的好坏。既要有协方差还要有方差，那么协方差矩阵自然而然就要出来了。

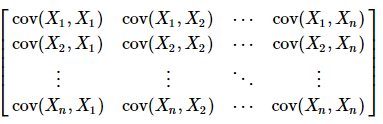
协方差矩阵计算公式：$cov(X_i,X_j)=\frac{1}{n?1}{\sum }_{i=1}^n(x_i?\bar{x}{)}^2=\frac{1}{n}X{X}^T,X:$样本矩阵，$Q^{?1}=Q^T$

这里向大家提一个问题，为什么协方差除以的是（n-1）而不是n呢？这个要是明白了，才是真的懂得了样本方差的真正含义
如果不太理解，可以点击我查看呦(点击查看样本方差)

上述协方差矩阵很完美的包含了自身方差与两两之间的协方差，天然是一个实对称矩阵，根据上述要求协方差为0 ，也就是说仅存在对角线元素。
矩阵论接着出来，实对称矩阵Q ?1=Q (T)，QCQ(T)=?,实对称矩阵可以转化为对角矩阵，n行n列实对称矩阵一定有n个单位正交特征向量，
因此Q就是我们要求的基，可以选定最大的d个特征值构造特征矩阵，从而将特征从n为降低至d维

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

dataset  = load_boston()
dataset.data.shape
features = dataset.data
target = dataset.target
# 先看下数据情况
pd.DataFrame(features,columns=dataset.feature_names)
# 数据分割
x_train,x_test,y_train,y_test = train_test_split(features,target,test_size=0.8,random_state=123)
# 特征工程
## 数据归一化(中心化)
standard = StandardScaler()
x_train = standard.fit_transform(x_train)
x_test = standard.transform(x_test)
# 计算协方差
cov = np.cov(x_train.T)
# 对协方差矩阵进行特征值分解
eigenvalues,eigenvectors = np.linalg.eig(cov)
# 根据特征值的数值大小的占比进行绘图
total = np.sum(eigenvalues)
occupy = [i/total for i in list(eigenvalues)]
plt.figure(figsize=(4,4),dpi=100)
plt.pie(x=occupy,labels=dataset.feature_names,autopct="%1.1f%%")

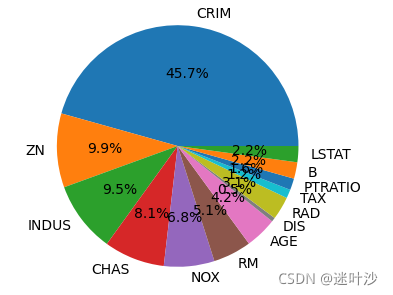
# 由上述可知，2维特征占据了其中的绝大部分信息，因此我们选择将特征由13维降至2维
# 选取特征值最大的前四维对应的特征值与特征向量
eigen = [(eigenvalue,eigenvectors[i]) for i,eigenvalue in enumerate(eigenvalues)]
# 按照特征值从大到小依次进行排序
eigen.sort(key=lambda x:x[0],reverse=True)
# 取前两个特征值对应的特征向量
w = np.hstack((eigen[0][1][:,np.newaxis],eigen[1][1][:,np.newaxis]))
# wx
x_train_pca = x_train.dot(w)
x_test_pca = x_test.dot(w)

from sklearn.linear_model import LinearRegression,SGDRegressor

# estimator  = LinearRegression()
esstimator = SGDRegressor(loss="huber")
# x_train.shape
# estimator.fit(x_train_pca,y_train)
estimator.fit(x_train,y_train)

estimator.score(x_train_pca,y_train)
# estimator.score(x_train,y_train)

y_pred = estimator.predict(x_train_pca)
# y_pred = estimator.predict(x_train)

ax = plt.gca()
# ax.plot(x_train_pca[:,0],y_pred,alpha=0.3)
ax.plot(y_pred,label='预测值')
ax.scatter(x=[i for i in range(len(y_train))],y=y_train,color="red",alpha=0.4)
# ax.scatter(x=[i for i in range(len(y_train))],y=y_pred,color="y",alpha=0.4)

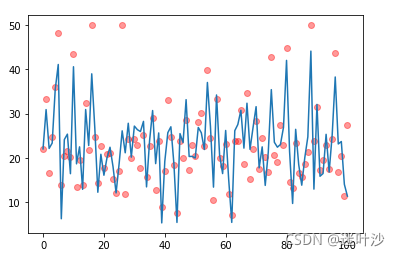
简单方法，直接调用sklearn封装的PCA算法

pca = PCA(n_components=2)
feature = pca.fit_transform(features)

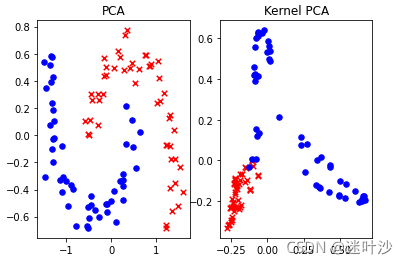
2-2：kernel PCA

核化PCA，其实和SVM中的核函数一致。就是有些数据本身在低纬情况下不可分，我们通过核函数将其扩展到高维空间或许就变得很容易划分。
回忆下SVM的核函数$K(x_i,x_j)=\phi (x_i)\phi (x_j)$,由于等式右边计算复杂繁琐，因此我们只需要找出一个核函数K即可大大简化计算进程。核PCA与PCA相比其实就多了一步，就是想使用核函数将数据投影到一个高维空间，然后再进行PCA。

from sklearn.decomposition import KernelPCA
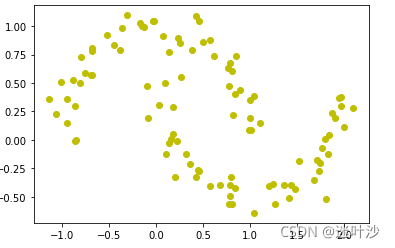
from sklearn.datasets import make_moons

# 创建月牙型数据
X,y = make_moons(n_samples=100,noise=0.1,random_state=111)
plt.figure()
plt.scatter(X[:,0],X[:,1],color="y")

pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
ker_pca = KernelPCA(n_components=2,kernel="rbf",gamma=10)
x_pca = ker_pca.fit_transform(X)
fig,ax = plt.subplots(nrows=1,ncols=2)
ax[0].scatter(X_pca[y==0,0],X_pca[y==0,1],color="red",marker="x",s=30)
ax[0].scatter(X_pca[y==1,0],X_pca[y==1,1],color="blue",marker="o",s=30)
ax[0].set_title("PCA")
ax[1].set_title("Kernel PCA")
ax[1].scatter(x_pca[y==0,0],x_pca[y==0,1],color="red",marker="x",s=30)
ax[1].scatter(x_pca[y==1,0],x_pca[y==1,1],color="blue",marker="o",s=30)
plt.show()