学习视频:[中英字幕]吴恩达机器学习系列课程
学习资料: https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
文章目录
1. 引言
1. 监督学习Supervised Learning

监督学习指的就是我们给算法一个数据集。这个数据集由“正确答案”组成。在房价的例子中,我们给了一系列房子的数据,我们给定数据集中每个样本的正确价格,即它们实际的售价然后运用学习算法,算出更多的正确答案。(回归Regression问题)

这里举的例子是依据肿瘤的尺寸来确定肿瘤是恶性还是良性。(分类Classification问题) 但往往分类依据的特征不止一个。例如:

我们加入了年龄作为评价的指标。显然我们可以加入很多的指标来让我们的分类更加的合理。(后续会介绍:SVM支持向量机)
2. 无监督学习Unsupervised Learning

上一个数据集中每条数据都已经标明是良性或恶性肿瘤。所以,对于监督学习里的每条数据,我们已经清楚地知道,训练集对应的正确答案,是良性或恶性了。
而在无监督学习中,我们已知的数据,不同于监督学习的数据的样子,即无监督学习中没有任何的标签。
针对数据集,无监督学习就能判断出数据有两个不同的聚集簇。这是一个,那是另一个。无监督学习算法可能会把这些数据分成两个不同的簇。所以叫做聚类(Clustering)算法。
2. 单变量线性回归 Linear Regression with One Variable
2.1 模型展示

线性回归算法:很好理解,根据已有的数据集来进行线性拟合,在给出一个x的值来预测y。

典型的监督学习实例,我们将训练集的数据输入到学习算法中,学习算法会拟合出一个函数?。? 代表 hypothesis(假设),因此 ? 根据输入的 𝑥值来得出 𝑦 值,𝑦 值对应房子的价格 因此,? 是一个从𝑥到 𝑦 的函数映射。
可以写成: ?𝜃(𝑥) = 𝜃0 + 𝜃1𝑥,
2.2 代价函数 Cost Function
函数构建出来了,那么是怎么确定参数 𝜃0 和 𝜃1的呢?
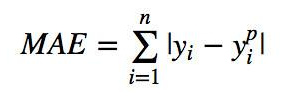
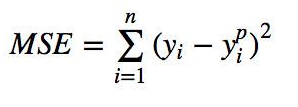
MAE 为绝对平均误差,可以反映出模型的准确性,MSE为均方误差,可以反映出模型的鲁棒性。

2.3 代价函数的直观理解

假设 𝜃0 为0,每一个 𝜃1对应了一个取值, 𝜃1=0时,损失J(0)=(1^2 + 2^2 + 3^2)/6。依次作点可得到右图,于是我们选择代价函数最低的值作为 𝜃1 和最优值。
当然,我们真正需要的是一种有效的算法,能够自动地找出这些使代价函数 𝐽 取最小值的参数 𝜃0 和 𝜃1 来。
2.4 梯度下降 Gradient Descent
梯度下降是一个用来求函数最小值的算法,我们将使用梯度下降算法来求出代价函数 𝐽(𝜃0, 𝜃1) 的最小值。
梯度下降背后的思想是:开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛),计算代价函数,然后我们寻找下一个能让代价函数值下降最多的参数组合。

学习率的设置要求很高,设置过低的话,需要很久才能达到全局最优点;设置过高的话,容易震荡达不到最优解。

而当你设置完成学习率后,就不需要再改动了。后一项的偏导会随着斜率的降低而减小,直到达到最优解时减小为0。
值得指出的是,梯度下降并未穷尽组合,因而无法确定是局部最优还是全局最优。如下图:

2.5 梯度下降的线性回归
将上述两种方法合在一起,简单的求偏导。

3. 多变量线性回归 Linear Regression with Multiple Variables
3.1 多维特征 Multiple Features
映衬上面所说的,我们将特征的类别增多,就构建了一个多变量的模型。

4.2 多变量梯度下降 Gradient Descent for Multiple Variables
不过是未知变量变多了而已。


4.3 特征缩放 Feature Scaling和学习率 Learning Rate
以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000 平方英尺,而房间数量的值则是 0-5,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。 如右图。

4.4 特征和多项式回归 Polynomial Regression
举了两个例子


通常我们需要先观察数据然后再决定准备尝试怎样的模型。
注:如果我们采用多项式回归模型,在运行梯度下降算法前,一定要进行特征缩放。
5. 逻辑回归 Logistic Regression
5.1 分类Classification

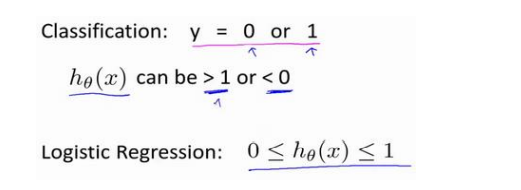
很明显可以看出来,如果我们使用线性回归解决分类问题。当尺寸过大时,可以看到y明显大于1了。但我们的标签是离散的0,1。
综上,线性回归并不是解决分类问题的好方法。
5.2 假说表示
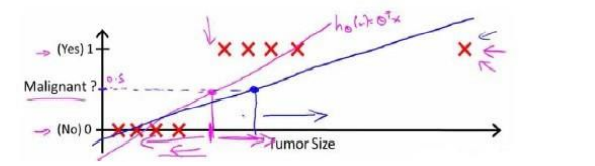
只看粉紫色的线:
根据线性回归模型我们只能预测连续的值,然而对于分类问题,我们需要输出 0 或 1。于是规定如下:
当?𝜃(𝑥) >= 0.5时,预测 𝑦 = 1。
当?𝜃(𝑥) < 0.5时,预测 𝑦 = 0 。
但当我们引入一个极端数据后,回归线变成了蓝色的:
此时在使用0.5作为阈值来预测肿瘤是良性还是恶性便不合适了。因该调小一点。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在 0 和 1 之间。 逻辑回归模型的假设是: ?𝜃(𝑥) = 𝑔(𝜃𝑇𝑋) 其中: 𝑋 代表特征向量。𝑔 代表逻辑函数,(logistic function)是一个常用的逻辑函数为 S 形函数(Sigmoid function),公式为:
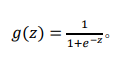


?𝜃(𝑥)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1 的可能性(estimated probablity),即 ?𝜃(𝑥) = 𝑃(𝑦 = 1|𝑥; 𝜃)
例如,如果对于给定的𝑥,通过已经确定的参数计算得出?𝜃(𝑥) = 0.7,则表示有 70%的几率𝑦为正向类,相应地𝑦为负向类的几率为 1-0.7=0.3
总结:因为线性回归的预测是一个连续的解。但是分类问题通常是离散的解。因此,将线性回归输出的连续解加以sigmoid进行标准化,结合预测的规定,使得输出得结果符合离散的分类指标,进而进行分类。
5.3 判定边界 Decision Boundary
在逻辑回归中,我们预测:
当?𝜃(𝑥) >= 0.5时,预测 𝑦 = 1。
当?𝜃(𝑥) < 0.5时,预测 𝑦 = 0 。
根据上面绘制出的 S 形函数图像,我们知道当
𝑧 = 0 时 𝑔(𝑧) = 0.5
𝑧 > 0 时 𝑔(𝑧) > 0.5
𝑧 < 0 时 𝑔(𝑧) < 0.5
又 𝑧 = 𝜃𝑇𝑥 ,
即:𝜃𝑇𝑥 >= 0 时,预测 𝑦 = 1
𝜃𝑇𝑥 < 0 时,预测 𝑦 = 0

𝜃和x应该都是列向量,这样𝜃𝑇*x才是目标函数。

生成的决策边界就是上图的分隔线。
5.4 代价函数 CostFunction
根据线性回归的确定最优参数的方法,我们也同样希望梯度下降法可以用来求解该函数的参数最优解。


5.5 简化CF和梯度下降
找出一种稍微简单一点的方法来写代价函数:



如果有n个特征,则𝜃为一个1*n的列向量,并且同时更新所有𝜃的值。

现在,如果你把这个更新规则和我们之前用在线性回归上的进行比较的话,你会惊讶地发现,这个式子正是我们用来做线性回归梯度下降的。
那么,线性回归和逻辑回归是同一个算法吗?要回答这个问题,我们要观察逻辑回归看看发生了哪些变化。实际上,假设的定义发生了变化。
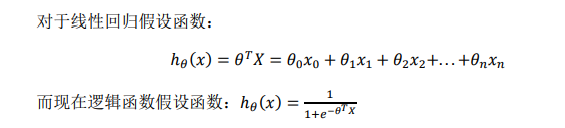
因此,即使更新参数的规则看起来基本相同,但由于假设的定义发生了变化,所以逻辑函数的梯度下降,跟线性回归的梯度下降实际上是两个完全不同的东西。
5.6 多类别分类:一对多 Multiclass Classification_ One-vs-all

我们先从用三角形代表的类别 1 开始,实际上我们可以创建一个,新的"伪"训练集,类型 2 和类型 3 定为负类,类型 1 设定为正类,我们创建一个新的训练集,如下图所示的那样,我们要拟合出一个合适的分类器

同理,对其余两个数据簇做同样的操作,我们就可以得到3个分类机。

6. 正则化 Regularization
6.1 过拟合 Overfitting

优化方式:
① Reduce number of features
(1)人工选择保留主要的特征(2)模型选择算法
② Regularization
保持所有特征,但减少量级和参数
6.2 代价函数 CostFunction
上面的回归问题中如果我们的模型是:
?𝜃(𝑥) = 𝜃0 + 𝜃1𝑥1 + 𝜃2𝑥2^2 + 𝜃3𝑥3^3 + 𝜃4𝑥^4
因为高次项产生了过拟合的产生,所以在一定程度上限制𝜃3,𝜃4,可以修改代价函数,对高次项系数设置一点惩罚。

6.3 正则化的线性回归 Regularized Linear Regression

6.4 正则化的逻辑回归 Regularized Logistic Regression

和之前的回归和代价函数对比一下:

可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令𝜃值减少了一个额外的值。
