开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 图形 2.4 传统经验光照模型详解（PBR光照计算公式介绍） -> 正文阅读

[人工智能]图形 2.4 传统经验光照模型详解（PBR光照计算公式介绍）

参考视频：
图形 2.4 传统经验光照模型详解
 GAMES101-现代计算机图形学入门-闫令琪 P15
参考资料：
PBR-learnopengl
彻底看懂PBR/BRDF方程-知乎
 辐射强度、辐亮度、辐照度——一文搞定
 辐射照度、辐射强度、光照度、发光强度（差异以及如何相互转换）（易懂讲解）
【基于物理的渲染（PBR）白皮书】（一）开篇：PBR核心知识体系总结与概览
 【实时渲染】菲涅尔反射率
 PBR以及在Disney和UE渲染模型中的使用
 Adopting a physically based shading model这篇文章提供了大量的论文参考
 Physically Based Shading at Disney
Real Shading in Unreal Engine 4

作业

1.能量守恒在光照模型中的作用
PBR（基于物理的渲染）是对现实近似模拟的渲染技术，旨在物理上合理地模拟光照效果，因此效果往往比非pbr渲染要好
PBR模型前置理论基础：微表面理论，能量守恒，菲涅尔反射

微表面理论

微表面理论认为任何平面都是由极小的“微平面组成”

在微观层面上没有任何表面是完全光滑的，但鉴于这些微表面足够小，我们无法在每个像素的基础上区分它们，我们用一个“粗糙度”参数来估计微表面的粗糙度。再根据微表面的粗糙度，我们可以计算出微平面法线m与向量h一样的微平面的比例（这个比例具体如何计算后文会解释），这个h（halfway vector）也是blinn-phong模型使用到的半角向量，h的计算方式如下图（l:表面指向光源方向 v:表面指向视线方向）
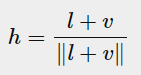
在这里插入图片描述
从下图中可以看到只有法线等于h的微平面才能使光线反射到视线上。因此只要知道出与向量h一样的微平面的比例，就可以知道有多少微平面对观察者观察到的颜色有贡献

粗糙度越大镜面反射范围越大，更暗；越小反射范围越小，越亮

微平面理论近似的遵循能量守恒定律：出射光的能量不能大于入射光的能量。（从上图也能看出，高光范围小更亮，范围大更暗）所以遵循能量守恒定律是为了让场景看起来更符合物理，更真实

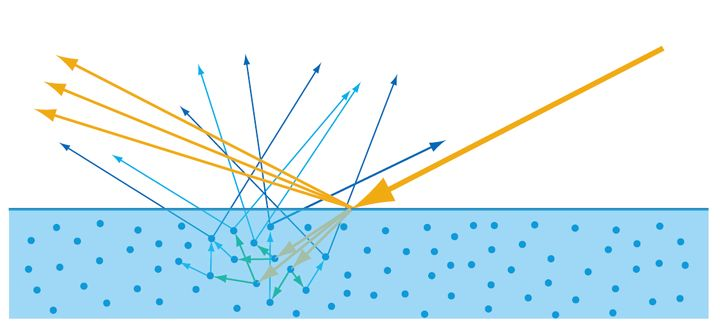
微平面理论说明光线在交界点处会在多个方向上产生反射和折射光。

菲涅尔反射

想象观察一个湖面，远看（入射角大）树的倒影（反射）很清晰，近看（入射角小）湖面下的鱼（折射）清晰。可见随着入射角增大（从近到远看），光的反射率单调上升，折射率单调下降。更容易看到物体表面上其他物体的倒影而很难看到物体内部的情况

菲涅尔公式则描述了一束光经过两个介质交界面分裂成反射光和折射光时，反射光与折射光占原光线的比例。（图中可正可负的意思是正负号与如何定义光线的正方向有关）
值得注意的是，折射光进入介质内部后可能会再次发生反射和折射，这部分被称为“次表面散射”，这些光部分会被吸收，部分会再次离开物体表面散射出去，形成漫反射。着色器用次表面散射可以以牺牲性能为代价显著改善皮肤，蜡或大理石等材料的视觉效果

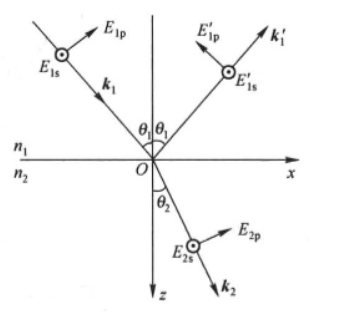
rs是反射光的垂直分量，rp是反射光的水平分量，ts是折射光的垂直分量，tp是折射光的水平分量

对于自然光，s波和p波的能量相等，因此自然光的反射率 $R_n=\frac{1}{2}(R_s^2+R_p^2)=\frac{1}{2}[\frac{sin^2(θ_1-θ_2)}{sin^2(θ_1+θ_2)}+\frac{tan^2(θ_1-θ_2)}{tan^2(θ_1+θ_2)}]$
当光线入射角趋近于0°（垂直于介质表面）时，有（n为折射率）
$\frac{tanθ_1}{tanθ_2}\approx\frac{sinθ_1}{sinθ_2}\approx\frac{θ_2}{θ_1}=n$
此时 $R_n=\frac{1}{2}(R_s^2+R_p^2)=(\frac{n-1}{n+1})^2$
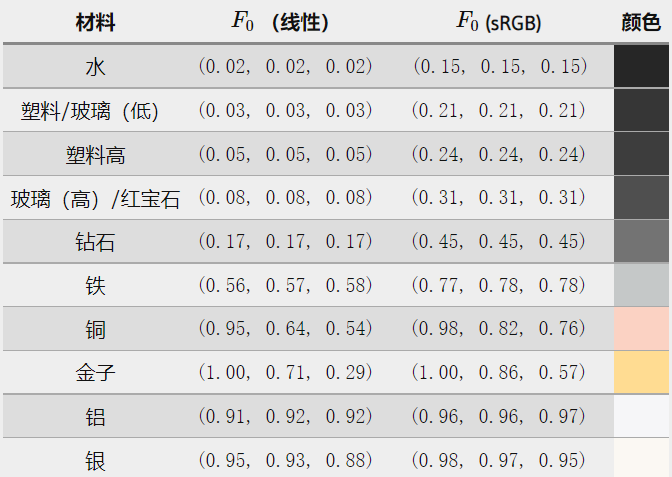
接近0°入射角时的菲涅尔反射率Rn（表示反射光占原光线的比例）被记作F0我们可以用上式，根据折射率（也称IOR）计算F0
不同材质其F0不同（线性和sRGB指色彩空间）,如下图所示

下图展示了不同波长和不同入射角下玻璃，铜和铝的菲涅尔反射率

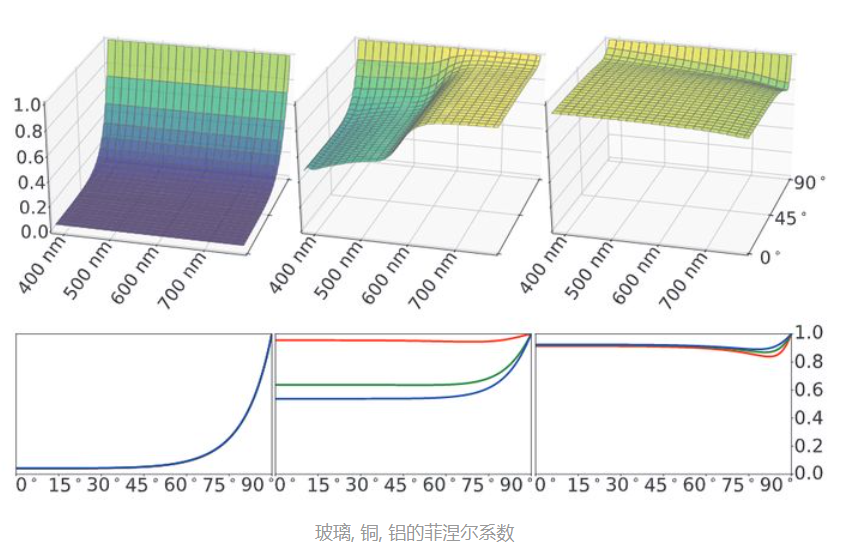
结合以上两图我们可以发现金属和非金属的菲涅尔反射有很大差异：

1.金属

·菲涅尔反射率会受到波长影响，需要引入复数来表示反射率，因此用Fresnel-Schlick近似(下文会介绍)时需要用rgb三个值（且这三个值不同，体现对不同光有不同的吸收率）表示
·反射率大部分在0.5和1之间，说明金属吸收了大部分折射光，其颜色主要是由镜面反射决定的

2.非金属（也被称为电介质）

·菲涅尔反射率与波长无关，因此F0只用一个值（一般取0.04）就能表示
·反射率几乎接近0，说明非金属的颜色主要是由漫反射（也就是折射光引起的次表面散射）决定的
（注意这里的漫反射和镜面反射是从微观角度上考虑的，看光线是反射光还是次表面散射光来区分，而平时说的漫反射和镜面反射从宏观上观察物体是否光滑来区分）

也许有人就会产生疑惑：根据微平面理论，直接反射光方向是多种多样的，那为什么这部分光不算漫反射而算镜面反射呢？
1.漫反射和镜面反射本质上都是光线，我们平时说的漫反射和镜面反射是从宏观角度观察物体，看物体表面是否光滑（光线是否集中），也就是根据结果来决定光线是镜面反射还是漫反射；而在PRB模型中，从微观角度观察光线，看光线是直接反射，还是次表面散射，也就是根据光线的路径决定光线是镜面反射还是漫反射
2.结合实际代码来理解，我们在像素着色器中计算BRDF，这里一个像素可以看作一个微元（一个微元有许多微平面），且拥有唯一一个法线，这个法线就代表这所有微平面法线的平均值，也就是说大体上微平面的法线都是与微元的法线一致，因此直接反射光主要集中在对称方向，且集中程度与粗糙度有关（可以看到当粗糙度变大，镜面反射的结果实际上就是我们从宏观角度所说的“漫反射”），所以用镜面反射描述直接反射光是比较精确的

reflectance equation反射比方程/渲染方程

该方程是目前模拟光的视觉效果的最佳模型，具体如下

该方程描述了一个极小的微元表面接受光照后发出的光的功率。让我们先来看看这些字母分别代表什么

p:辐射功率。指单位时间内辐射源所发射的总辐射能
单位瓦

ω:ωi表示入射光线（l），ω0表示出射光线（v），注意等号右边要积分的微元指的是立体角

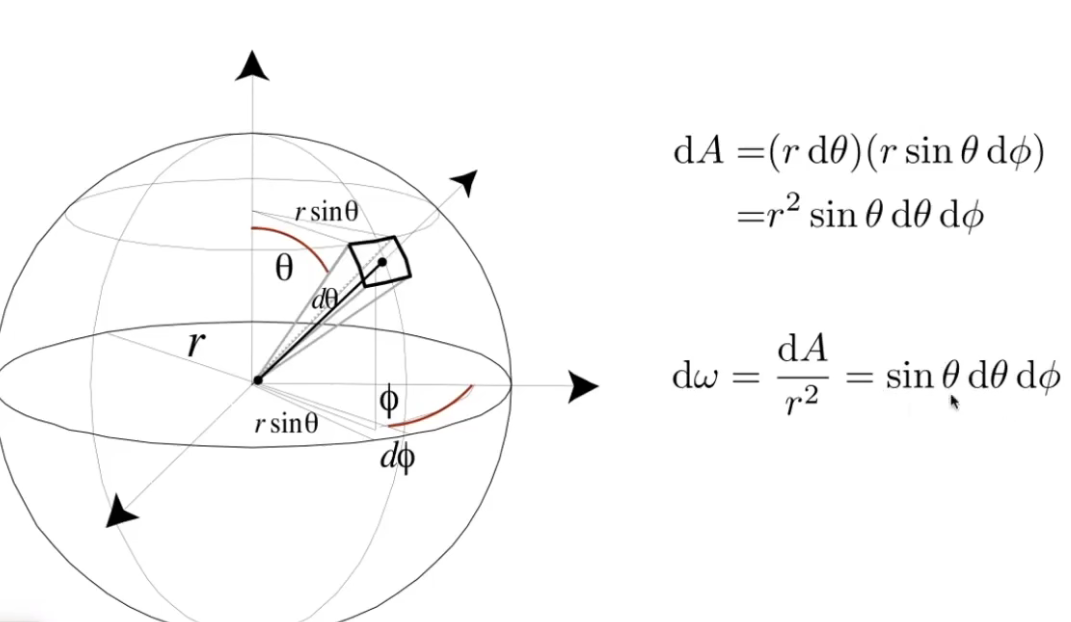
dω:立体角，是站在某一点的观察者测量到的物体大小的尺度
锥体的立体角大小定义为：以锥体的顶点为球心作球面，该锥体在球表面截取的面积与球半径平方之比，
单位球面度（一整个球的球面度为4π）
计算方式见下图

?

L:辐射亮度(radiance)，简称辐亮度。指面辐射源在单位时间内通过垂直面元法线方向n上单位面积、单位立体角上辐射出的能量，即辐射源在单位投影面积上、单位立体角内的辐射通量
计算方式：L=ddΦ/(dAdΩ·cosθ)，θ为立体角(solid angle)与法线之间的夹角
单位瓦/(球面度·米^2)
辐射亮度表示面辐射源上某点在一定方向上的辐射强弱的物理量

?

Φ:辐射通量。指单位时间内通过某一截面的辐射能
单位瓦(焦耳/秒)

E:辐射照度(Irradiance)，简称辐照度。指接收物体的单位表面积上接收到的辐射功率
单位瓦/米^2
计算方式见下图

?

下图直观地展示了这些物理量的区别和联系

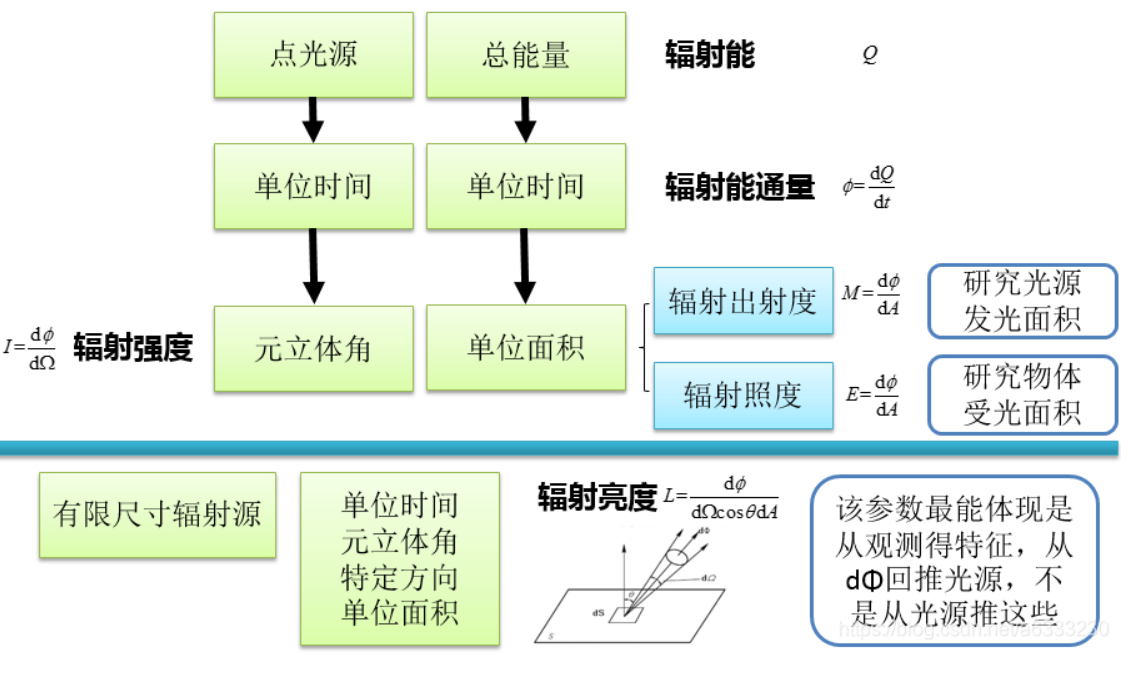
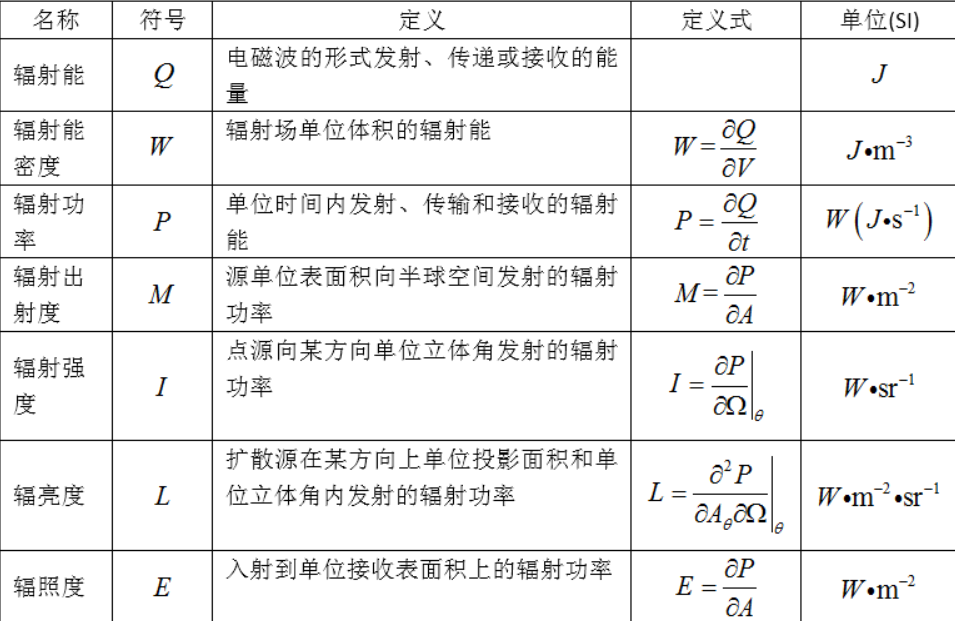
（注意这里的辐亮度计算中分母的dA已经是投影面积，与上面的微元计算公式L=ddΦ/(dAdΩ·cosθ)不同，后者的da是光源上的微元面积因此要乘cosθ，以将其转换到垂直于光线的平面，即与上图介绍辐射亮度的图中黄色平面平行）

了解了这些字母的含义之后我们再回看渲染方程

该方程本质上告诉我们，给定在物体（物体接受光照后发出光也能看作辐射源）上一点A和入射光的信息，就能计算出射光的辐亮度
·L0表示A点出射光的辐亮度
·fr表示出射光辐亮度和入射光辐照度的比例函数
fr有多种形式的函数可以模拟，大体分为如下几种
1.BRDF（双向反射分布函数）：仅处理受光面，且不考虑次表面散射（因为漫反射属于次表面散射，所以严格地讲只是简单地考虑次表面散射）。适合不透明材质。本文只介绍BRDF
2.BTDF（双向透射分布函数）：仅处理背光面，且不考虑次表面散射。
3.BSDF（双向散射【反射+透射】分布函数）：处理受光面和背光面，且不考虑次表面散射。适合透明度比较高的材质。
4.BSSRDF（双向散射表面反射率分布函数）：处理受光面和背光面，考虑次表面散射，适合半透明材质，云，玉石，牛奶等。

·ωi表示入射光线光线方向l），w0表示出射光线（特指视线方向v）
·Li表示A点入射光的辐亮度，与fr函数相乘，再乘上n·ωi即可得到出射光的辐亮度L0
·n·ωi指入射光线和法线之间的夹角的余弦值，用于将入射光的辐亮度Li转换为辐照度E
·∫Ω dωi则是入射光半球的积分（因为光不可能同时照亮微元的两个面，所以是半球而不是整个球，这里的光并没有指定光源的种类，只要是从微元的正半球照射进来的光线都要考虑），可以理解为对入射半球上所有的ωi进行累加
fr的推导见彻底看懂PBR/BRDF方程 2. BRDF到底是啥?
接下来讨论怎么具体表示BRDF（fr函数）
BRDF分为diffuse（漫反射）和specular（镜面反射）两项

1.diffuse BRDF（漫反射）

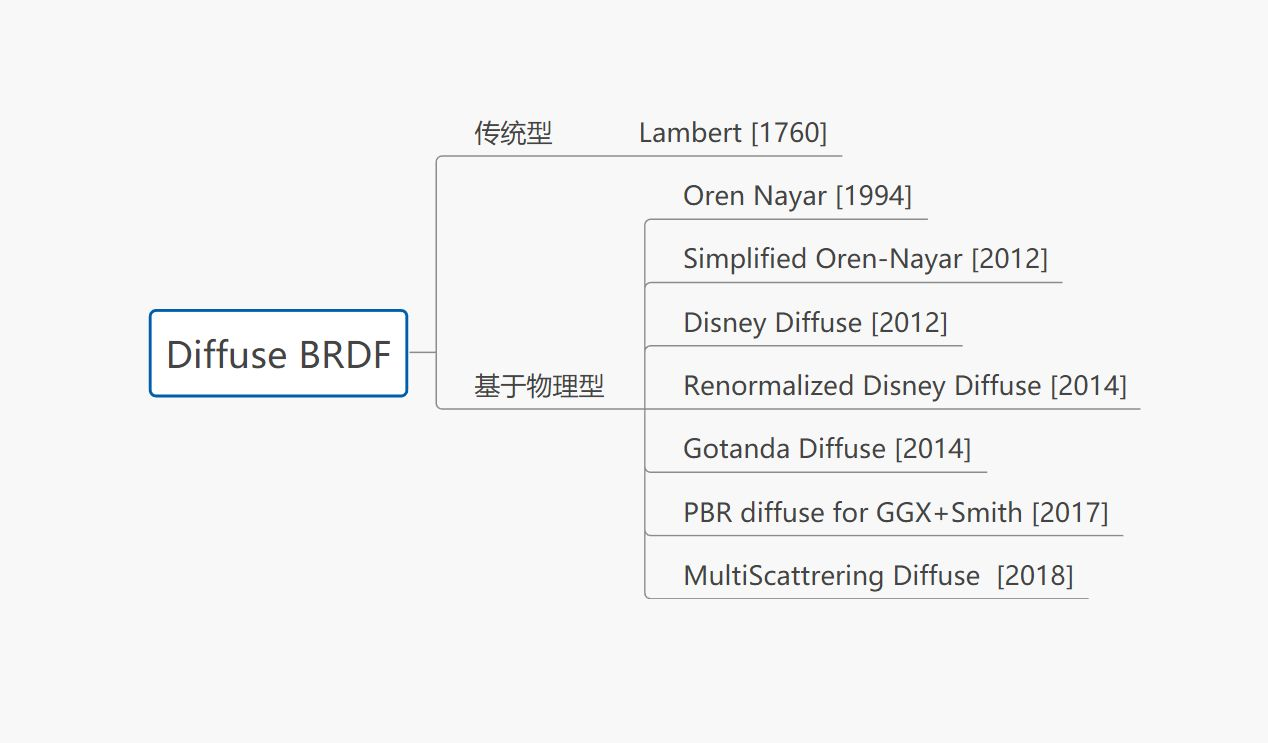漫反射的计算方法大体分为两种，基于经验（如Lambert（朗伯/兰伯特））和基于物理。

1.Lambert diffuse
Lambert diffuse适用于朗伯辐射体：辐射源各方向上的辐射亮度不变，辐射强度随观察方向与面源法线之间的夹角θ的变化遵守余弦规律。
表达式如下:

$f_{lambert}=\frac{C_{diffuse}}{π}$
（Cdiffuse是材质本身的颜色，也被称作albedo（反射率）/basecolor（基础色）/surfaceColor（表面颜色））
正向推导：

可能会有人感到疑惑：这个Lambertian好像和我们说的兰伯特漫反射（n·l）不一样，但是我们令fr=c/π代回到反射比方程中，可以发现积分后π就被抵消掉了，而且乘上后面的n·ωi正好就是传统的lambert漫反射光照模型。因此我们可以把分母看作一个为了满足能量守恒定律而引入的归一化因子

2.Disney diffuse

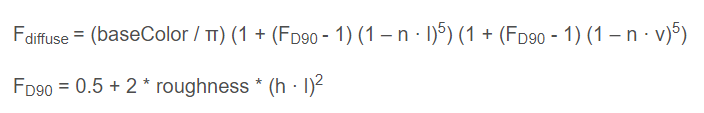
FD90指的是法线和视线呈90°时的菲涅尔反射率

2. specular BRDF（镜面反射）

目前业界广泛采用的基于微表面理论的Microfacet Cook-Torrance BRDF模型，公式如下（l:表面指向光源方向，v:表面指向视线方向，h:半角向量（微平面法线），n:微元法线）：
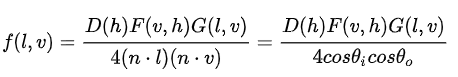
在这里插入图片描述

（推导见[彻底看懂PBR/BRDF方程-知乎 7.镜面反射的BRDF如何推导？]）(https://zhuanlan.zhihu.com/p/158025828)

可以看到该公式由分子的三个符号和分母的一个归一化因子组成，其中分子的DFG各代表微平面表面特性的一个近似描述的函数

D：Normal distribution function（NDF）法线分布函数

法线分布函数表示法线与半角向量方向相同的点微平面占微元的比例
目前常用的是Disney的Trowbridge-Reitz（各向同性的GGX）模型，其中α是控制参数，这里α通常表示roughness^2（由roughness粗糙度对α进行映射，当然令α=roughness也没问题，毕竟roughness是手动控制的参数）（粗糙度在0-1之间，越大越粗糙）
在这里插入图片描述
GGX优点：1.成本低廉 2.更长的拖尾显得更自然

其他NDF模型（m是微平面法线，这里指半角向量h）
在这里插入图片描述

F：Fresnel equation菲涅尔方程

菲涅尔方程表示反射到视线方向上的光占入射光的比例，菲涅尔方程是一个相当复杂的方程，一般我们用Fresnel-Schlick近似表达菲涅尔反射率F
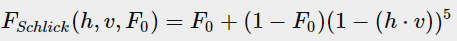
在这里插入图片描述
其中h是半角向量（也就是微平面的法线），v是入射光方向矢量,h·v用于求入射角的余弦值,F0是接近0°入射角时的菲涅尔反射率（上文介绍过如何求F0）
ue4在2013siggraph上给出了这个形式的略微优化版本
lut

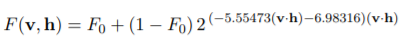
G：Geometry function几何函数（阴影遮罩函数）

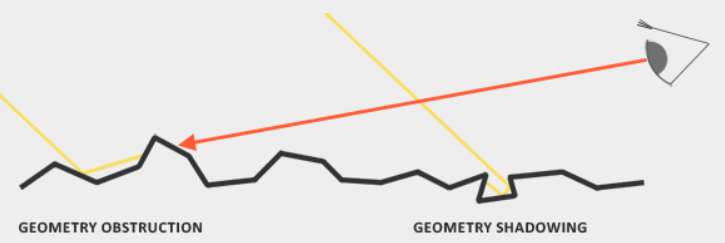之前讲微平面理论的时候提到过只有法线等于h的微平面才对brdf做出贡献,但是法线等于h的微平面中可能会有一部分发出的反射光被其他微平面给阻挡，而几何函数就是描述法线等于h且未被遮蔽的微平面占微元的百分比。

1.Schlick-GGX模型
Schlick-GGX模型是GGX和Schlick-Beckmann的的结合：
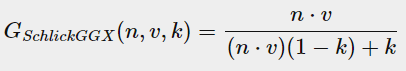
在这里插入图片描述
其中K是对α（注意α与roughness的转换可能因引擎而异，下图的α实际上就是指roughness）的重新映射，与场景使用直接照明还是IBL（基于图像的照明，后文介绍环境光时会介绍）有关，这里反射率方程用于描述直接光，取(α+1)^2/8
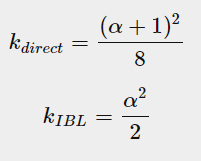
在这里插入图片描述
考虑到视线方向的几何遮挡和光方向矢量的几何阴影，我们根据Smith方法来包含两者得到最终的G值（Gsub指的就是Gschlick-GGX）：

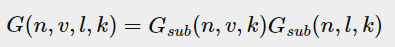
这个模型也是ue在siggraph2013 ue 第29幅图也提到过

2.Cook-Torrance模型
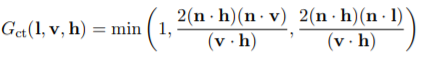
在这里插入图片描述
3.Implict

想了解更多的diffuse和specular模型计算方式可以参考这两篇
UE4中的基于物理的着色（一）
镜面反射BRDF模型(Specular BRDF)及实现效果

将漫反射与镜面反射合并

Cook-torrance模型提供了一种方案（据learnopengl所述）
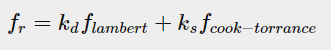
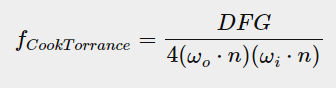
在这里插入图片描述

其中 ωi表示入射光向量(l)，ω0表示出射光向量(v)，kd是漫反射系数，ks是镜面反射系数（菲涅尔反射率），kd=1-ks（考虑到能量守恒。kd和ks表示入射光照射到物体表面微元后分配给漫反射和镜面反射的比例）
考虑到F实际隐含了Ks（F表示在v方向上的镜面反射光占入射光的比例，所以F包含了Ks），因此代入的过程中Ks应该删去，实际公式如下：
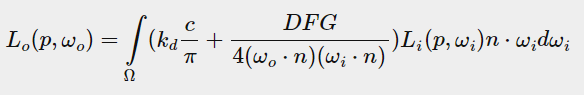
在这里插入图片描述
·对于电介质，kd=1（尽管理论上应该是取1-F0但ue4也取1），F0一般取（0.04，0.04，0.04）就能代表大部分电介质的特性。
·对于导体/金属，我们引入了一个metalness（金属度）可控参数来对F0进行插值：
? ? ? ? ? ? ? ? ? ? ? ? ? F0 = mix((0.04,0.04,0.04), albedo, metalness)
? ? ? ? ? ? ? ? ? ? ? ? ? kd=1-metalness
（可以看到metalness=0时F0=0.04（等价于电介质），metalness=1的时候则采用金属自身的反射率（F0）且没有漫反射）

总结：直接光照就是上面的反射率公式，对于物体表面上的一个微元。给定微元法线正向的半球上所有的入射光的功率，我们可以得到物体在接收入射光后最终在视线方向上发出的光的功率。
在实际代码编写中，如果用反射率方程计算直接光照，环境光照另外单独计算，我们可以使用如下等价公式来简化只有直接光照的反射率方程：（中间的运算符表示对两边的矩阵或向量中的每个一一对应的元素直接相乘，Clight指光源颜色）
在这里插入图片描述
解析：Clight光源颜色与波长相关，波长与能量成反比，在相同时间内，能量与功率成正比，所以这里的L0（V）可以看作最终物体表面微元的颜色
翻译如下：

环境光

除了直接光以外我们还需要环境光（来自环境其他物体的光，默认等同于间接光），在传统经验光照模型中我们用一个常数来代替，在PBR中我们用反射率方程更精确地描述环境光对物体的影响（环境光与直接光很大的区别是，直接光方向是确定的，而环境光方向是来自四面八方其他物体的反射光的）
在这里插入图片描述
先介绍环境光照的表示形式
我们需要一种方式来表示来自各个方向的环境光的辐亮度（假设各个方向的环境光照都是来自无穷远处的）
1.球谐函数：详细介绍
2.球形高斯：详细介绍（中文翻译版本：SG Series Part 2: 球形高斯基础）
我们可以用一张图片来记录这些球形函数，这种图片叫做环境贴图
1.经纬度贴图
2.球形贴图
3.立方体贴图
（更具体的介绍请参考这篇）

了解环境光照的表示形式后我们再来看环境光影响物体的表达式

环境光的反射率方程与直接光照的一样
在这里插入图片描述
可以看到漫反射和镜面反射可以拆分，于是变成如下形式

环境光的漫反射与镜面反射需要用到预计算的贴图来存储信息，因此也被称为IBL（基于图像的光照），接下来我们分别详细讨论。

环境光-漫反射

对于漫反射部分，将常数移到外面，得到如下形式：
在这里插入图片描述
在直接照明-漫反射中，因为入射光线是确切知道方向的，所以很容易求出射光方向的辐亮度L0。但是环境光-漫反射中，对于每一个微元而言，来自周围环境的入射光不是唯一的。每个入射光方向wi都可能会有辐射，所以求解积分很复杂，这也给我们提出了两个要求：
1.需要一个方法来检索任何wi方向的环境光辐射度
2.求解积分必须实时快速
下面重点介绍一种解决方案–立方体贴图
·1.立方体贴图（cube mapping）
立方体贴图是事先预计算来自各个方向入射光的辐亮度Li，并存储到一张立方体贴图中（一个纹素对应一个出射光方向ω0）。
预计算方式：
对于每一个出射光ω0，我们构建一个正向的半球，在其中离散的取大量不同方向的入射光ωi并采样，然后求平均，得到的结果作为出射光ω0的辐照度，将出射光方向作为索引，结果以颜色值的形式存储在立方体贴图中

因此这张立方体贴图也被称为辐照度环境贴图（irradiance map，也有把Irradiance Environment Mapping翻译成辉度环境映射的，明显要么瞎翻译，要么故意翻译成高级词汇反而失去了可读性）
（辐射方程还依赖于辐照度环境贴图的中心位置p，在场景中不同的位置得到的辐照度环境贴图不一样。渲染引擎通过在整个场景中放置反射探针（reflection probes）来解决此问题，每个反射探针计算其自身周围环境的辐照度贴图。这样，对于任意位置处的辐照度就可以通过离其最近的几个反射探头的辐照度的插值来得到。现在我们假设总是从辐照度环境贴图的中心位处采样，不考虑插值的事情）
下图是立方体环境贴图和其生成的立方体辐照度贴图的实例（尽管特别像高斯模糊但并不是直接模糊处理）

具体如何生成？
参考：
我们把方程转换成如下形式：
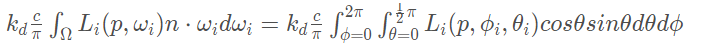
在这里插入图片描述

将积分转换为离散的累加和形式，n2对应不同的θ，n1对应不同的φ

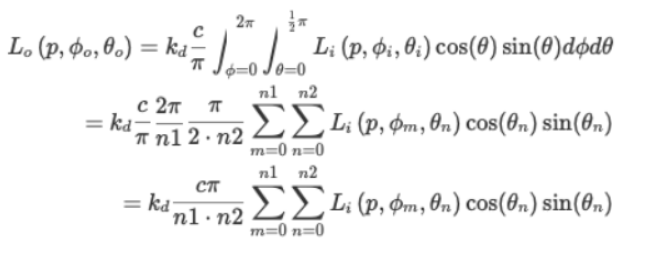
所以我们规定采样步长dθ和dφ就能对环境贴图进行采样，示例代码如下（来自LearnOpenGL学习笔记—PBR：IBL）：

============================Vertex   Shader=======================
#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texcoord;
layout (location = 3) in vec3 color;

out vec3 worldPos;

uniform mat4 viewMatrix;
uniform mat4 projectMatrix;

void main(){
	worldPos = position;
	gl_Position = projectMatrix * viewMatrix * vec4(position,1.0f);
}    
============================Fragment Shader=======================
#version 330 core
out vec4 FragColor;
in vec3 worldPos;

uniform samplerCube environmentMap;

const float PI = 3.14159265359;

void main()
{		
	// 世界向量充当原点的切线曲面的法线，与WorldPos对齐。
	// 给定此法线，计算环境的所有传入辐射。
    vec3 N = normalize(worldPos);

    vec3 irradiance = vec3(0.0);   
    
    // 计算切线空间
    vec3 up    = vec3(0.0, 1.0, 0.0);
    vec3 right = normalize(cross(up, N));
    up = normalize(cross(N, right));
       
    float sampleDelta = 0.025;
    float nrSamples = 0.0;
    for(float phi = 0.0; phi < 2.0 * PI; phi += sampleDelta)
    {
        for(float theta = 0.0; theta < 0.5 * PI; theta += sampleDelta)
        {
            // 球面到笛卡尔（在切线空间中）
            vec3 tangentSample = vec3(sin(theta) * cos(phi),  sin(theta) * sin(phi), cos(theta));
            // 切线空间到世界空间
            vec3 sampleVec = tangentSample.x * right + tangentSample.y * up + tangentSample.z * N; 

            irradiance += texture(environmentMap, sampleVec).rgb * cos(theta) * sin(theta);
            nrSamples++;
        }
    }
    irradiance = PI * irradiance * (1.0 / float(nrSamples));
    
    FragColor = vec4(irradiance, 1.0);
}

创建一个cube，将上述顶点着色器应用于该cube，则cube的6个面就是辐照度环境立方体贴图的6个面

·2.球谐函数SH（球谐函数还没看懂，这里给出一些参考资料）
参考：球谐光照——球谐函数
 Chapter 10. Real-Time Computation of Dynamic Irradiance Environment Maps（GPU Gems2）

·3.球形高斯SG
参考：SG Series Part 2: Spherical Gaussians 101
球谐函数与球形高斯的原理与立方体贴图本质上差不多，是用不同的方法存储光照信息

环境光-镜面反射

镜面反射部分如下：
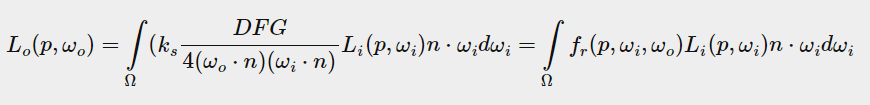
在这里插入图片描述
ks实际上不是一个常数，它取决于入射光方向ωi和视线方向v(ω0)（实际计算中因为F隐含了ks所以ks要删去，但是learnopengl在这里写的是ks，你可以把ks当作F来理解，菲涅尔系数取决于入射光方向ωi和视线方向v）。同样因为对各个方向的ωi和v进行积分过于复杂所以无法实时计算。Epic对此提出了一种解决方案，在做出一定妥协的情况下，为了实时计算的目的对镜面反射部分进行预卷积，这种方法被称为分解求和近似（Split Sum Approximation）
·分解求和近似
该方面将镜面反射积分拆解成两个单独的积分。左边称为预过滤环境贴图（Pre-filtered environment map），右边则是BRDF（环境光光BRDF描述镜面反射的部分），下面分别介绍。
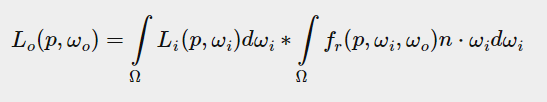
在这里插入图片描述
等式的右边也可以表示成累加和的形式

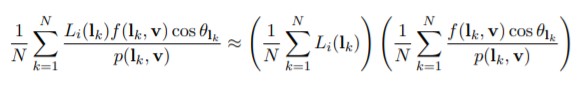
1.预过滤环境贴图（Pre-filtered environment map）

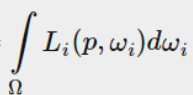
预过滤环境贴图跟辐照图贴图类似，是预先卷积计算过的环境贴图，但预过滤环境贴图考虑到了粗糙度（roughness）的影响。为了体现不同的粗糙度级别，环境贴图会使用更为分散的入射光向量（也叫采样向量）计算卷积以产生更模糊的镜面反射，我们将不同粗糙度的计算结果存入mipmap的不同级别中，如下图所示
在这里插入图片描述

生成预过滤环境贴图（重点：如何选择采样向量？）：
先引入几个概念（只是简单介绍，详细了解的话直接点击打开超链接）
大数定律（Law of Large Numbers）：简单理解为一个概率为P的事件做n次实验，实验次数越多，事件发生的频率越接近于概率P
蒙特卡洛积分（Monte Carlo）：用一组满足分布律f(x)的若干随机数对被积函数在积分区间内采样。蒙特卡洛积分建立在大数定律的基础上，式子如下
（f(x)是被积函数，pdf就是生成的样本的概率密度函数，N是采样次数，每一次采样得到一个xi带入式子中）
在这里插入图片描述
重要性采样（Importance Sampling）：蒙特卡洛积分选取的随机数（也叫采样点）集中在被积函数中对积分贡献较高的区域，而不是积分区间内均匀分布。这样选取可以减小方差，收敛速度快。

了解上面这些概念之后，我们再来看下面这幅图
在这里插入图片描述
可以看到镜面反射的波瓣尺寸随着粗糙度增加而变大。由于大多数光线都会集中在微平面法线向量h为中心的波瓣中，因此我们采样的光线（生成的样本向量）也应该满足这个规律（集中在波瓣中而不是像计算漫反射那样均匀取样本），这也被称为重要性采样

下面是ue中预过滤环境贴图的代码（R是镜面反射向量）
在这里插入图片描述
可以看到epic在此处令N=V=R，这是因为在卷积预过滤环境贴图的时候我们并不知道视线方向V，这的确意味着当我们从下图所示的角度观察时不会获得很好的镜面反射效果，但这通常被认为是合理的折衷方案

代码中Hammersley函数是生成随机数序列的一种方法，可以得到在[0,1]之间均匀分布的随机数序列（生成点在采样空间分布的均匀程度称作差异度Discrepancy，Hammersley属于低差异度序列），下面给出具体实现代码：(来自learn opengl)

float RadicalInverse_VdC(uint bits) 
{
    bits = (bits << 16u) | (bits >> 16u);
    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}

重要性采样的函数如下（Phi:φ，H：将球面坐标转换为笛卡尔坐标系）：
在这里插入图片描述

2.环境镜面反射BRDF
环境镜面反射与环境漫反射求解思路相同，也是对大量入射光进行采样来预计算光照信息
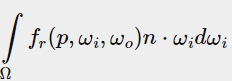
在这里插入图片描述
其中

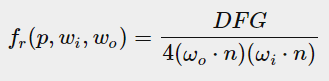
这个卷积要求我们同时考虑到入射角（n·ω0），表面粗糙度（影响fr中G和D项）和菲涅尔系数F0（与入射光矢量ω0）,对3个变量卷积实在复杂，但是我们可以对方程做点变换，先试着将F项移出方程
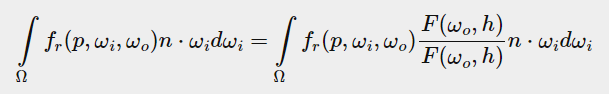
在这里插入图片描述
将分母移到fr下

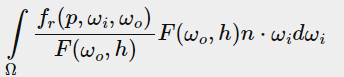
F项根据之前讲过的 Fresnel-Schlick计算

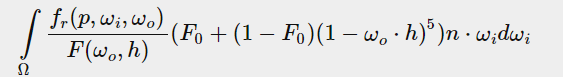
为了式子看上去更简洁，我们用α表示（1-ω0·h）^5，之后再变形

我们可以把最后一行式子拆成两项

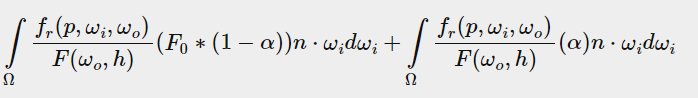
重新把α替换回来

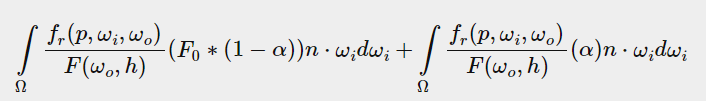
我们把fr/F替换成一个新的fr，这个新的fr已经不含菲涅尔项F了；同时我们把F0常数移到积分外面，最终式子如下
在这里插入图片描述
这条函数形如F0*a+b,因此我们称左边积分为F0_Scale（缩放系数）,右边积分为F0_bias（偏移）。根据这条函数，我们就可以计算每一个像素（微元）的环境光镜面反射值，返回类型为float2/vec2，我们以颜色的形式（scale当作r，bias当作g）存储在一张贴图上，用roughness和 NdotV表示纹理索引/位置（这张贴图被称为2D LUT/2D查找纹理,也叫BRDF混合贴图（BRDF integration map））。示例图和代码实现如下（来自learn opengl，UE实现的方法是一样的）
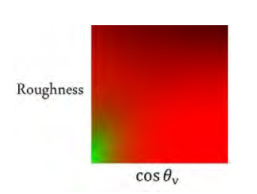
在这里插入图片描述

vec2 IntegrateBRDF(float NdotV, float roughness)
{
    vec3 V;
    V.x = sqrt(1.0 - NdotV*NdotV);
    V.y = 0.0;
    V.z = NdotV;

    float A = 0.0;
    float B = 0.0;

    vec3 N = vec3(0.0, 0.0, 1.0);

    const uint SAMPLE_COUNT = 1024u;
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);//normalize(reflect(-V, H));

        float NdotL = max(L.z, 0.0);
        float NdotH = max(H.z, 0.0);
        float VdotH = max(dot(V, H), 0.0);

        if(NdotL > 0.0)
        {
            float G = GeometrySmith(N, V, L, roughness);
            float G_Vis = (G * VdotH) / (NdotH * NdotV);
            float Fc = pow(1.0 - VdotH, 5.0);

            A += (1.0 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    A /= float(SAMPLE_COUNT);
    B /= float(SAMPLE_COUNT);
    return vec2(A, B);
}


// ----------------------------------------------------------------------------
float GeometrySchlickGGX(float NdotV, float roughness)
{
    // G_ShclickGGX(N, V, k) = ( dot(N,V) ) / ( dot(N,V)*(1-k) + k )
    float a = roughness;
    float k = (a * a) / 2.0;

    float nom   = NdotV;
    float denom = (NdotV * (1.0 - k) + k) + 0.0001f;//防止分母为0

    return nom / denom;
}
// ----------------------------------------------------------------------------
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

这里解释一下float G_Vis = (G * VdotH) / (NdotH * NdotV) 是怎么来的
首先这里的G_Vis根据公式其实指的就是去除F项后的fr，fr=G·D/（4·NdotH · NdotV）根据重要性采样的公式，还需要除掉pdf（概率密度函数），在这里pdf=D·NdotH/（4·VdotH）(参考UE4文档，代入即可得到G_Vis

别忘了之前在介绍直接光G项的时候提到过，K值与粗糙度α的关系，因此这里用IBL的方式计算环境光的时候，k=（α^2）/2
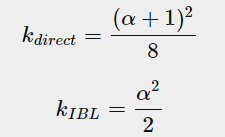
在这里插入图片描述
总结：在计算环境光BRDF项时，由于要对入射角（n·ω0，代码中的NdotV），表面粗糙度roughness（影响fr中G和D项）和菲涅尔系数F0(与入射光矢量ω0)三个变量积分（补充：尽管roughness与被积微元dω0没关系，但是每一个像素可能都有不同的粗糙度，因此在积分中也要考虑不同roughness的影响）过于复杂，因此采用预计算的方式，得出不同入射角、不同粗糙度下F0的值，将这些信息存储在一张贴图（称为LUT查找纹理）中。
在使用时，我们用NdotV和roughness对这张LUT采样，最终环境光BRDF的值为F0*LUT.r+LUR.g
————————
得到预过滤环境贴图与环境光BRDF项后，将两者相乘得到环境光-镜面反射值（这里的SpecularColor就是指F0），最终基于IBL的环境光-镜面反射的代码如下
在这里插入图片描述