[人工智能]吴恩达·Machine Learning || chap12 Support Vector Machines简记

12-1 Optimization objective

Alternative view of logistic regression

$$h_{\theta }(x)=\frac{1}{1+e^{?{\theta }^{T}x}}$$

If $y=1$,we want $h_{\theta }(x)\approx 1,{\theta }^{T}x?0$

If $y=0$,we want $h_{\theta }(x)\approx 0,{\theta }^{T}x?0$

? Cost of example:$$?(y\log h_{\theta }(x)+(1?y)\log (1?h_{\theta }(x)))$$$$=?y\log \frac{1}{1+e^{?{\theta }^{r}x}}?(1?y)\log (1?\frac{1}{1+e^{?{\theta }^{r}x}})$$

Support vector machine

Logistic regression:
$$mi{n}_{\theta }\frac{1}{m}[\sum _{i=1}^m{y}^{(i)}(?\log h_{\theta }(x^{(i)})+(1?y^{(i)})(?\log (1?h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
support vector machine:

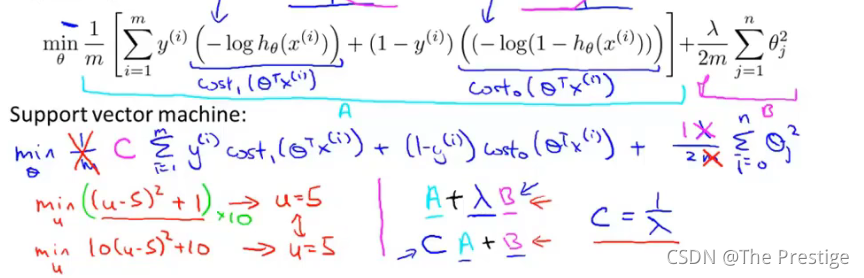
$$mi{n}_{\theta }C\sum _{i=1}^m[y^{(i)}{cost}_1({\theta }^T{x}^{(i)})+(1?y^{(i)}){cost}_0({\theta }^T{x}^{(i)})]+\frac{1}{2}\sum _{i=1}^n{\theta }_j^2$$

SVM hypothesis
$$mi{n}_{\theta }C\sum _{i=1}^m[y^{(i)}{cost}_1({\theta }^T{x}^{(i)})+(1?y^{(i)}){cost}_0({\theta }^T{x}^{(i)})]+\frac{1}{2}\sum _{i=1}^n{\theta }_j^2$$
Hypothesis:

$h_{\theta }(x)=\{\begin{array}{l}1if{\theta }^{T}x\ge 0\\ 0otherwise\end{array}$

12-2 Large Margin Intuition

Support Vector Machine

if $y=1$,we want $\theta^Tx\ge1\quad(\text{not just $\ge$ 0})$

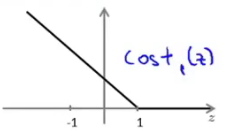
if $y=0$,we want $\theta^Tx\le-1\quad(\text{not just $<$ 0})$

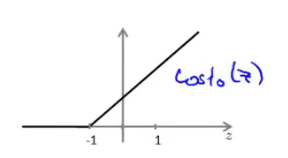
SVM Decision Boundary

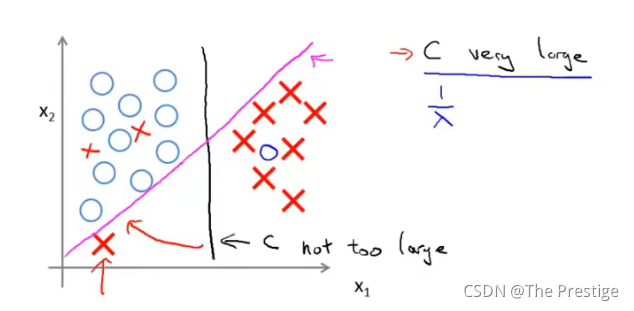
SVM Decision Boundary: Linearly separable case

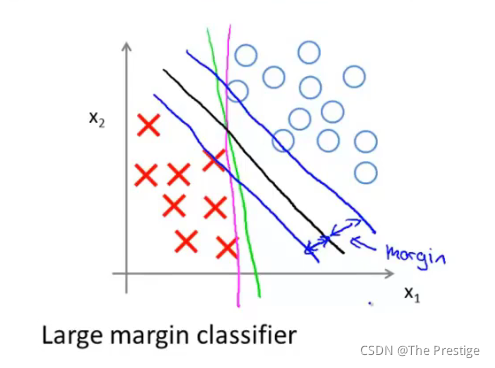
Large margin classifier in presence of outliers

12-3 The mathematics behind large margin classification (optional)

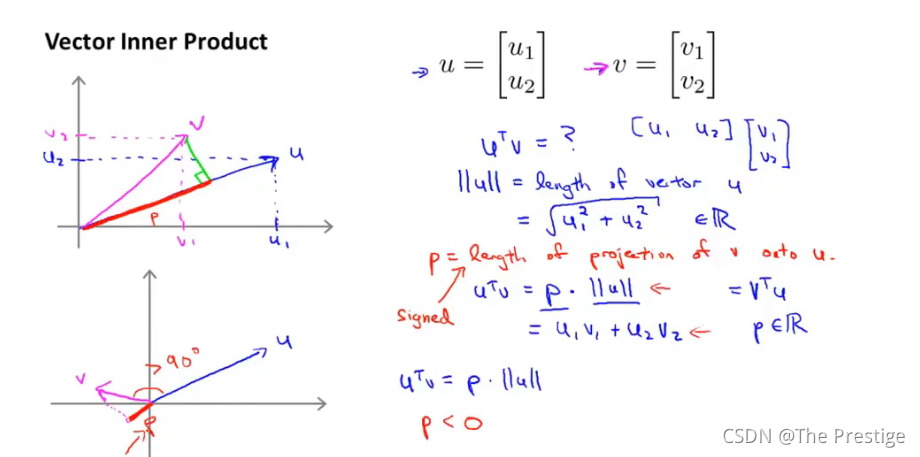
Vector Inner Product 向量内积

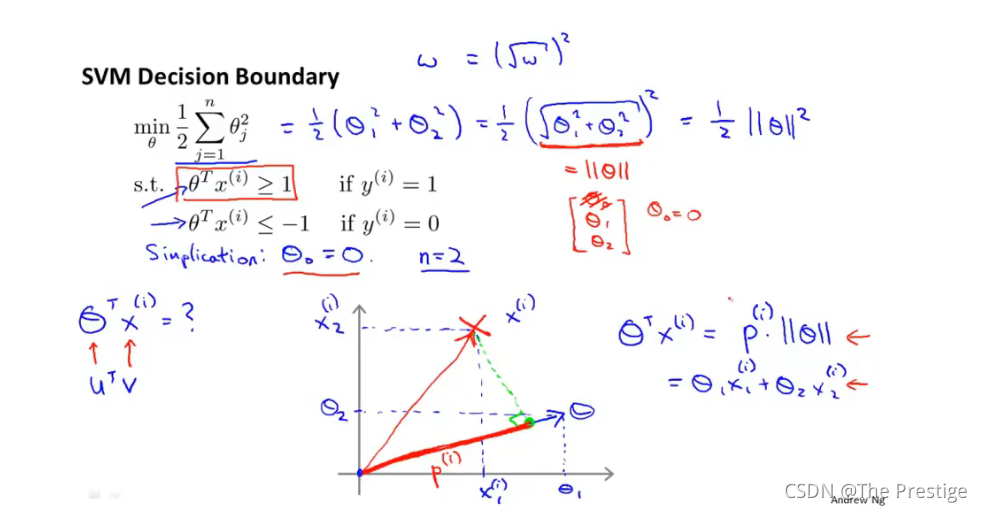
SVM Decision Boundary

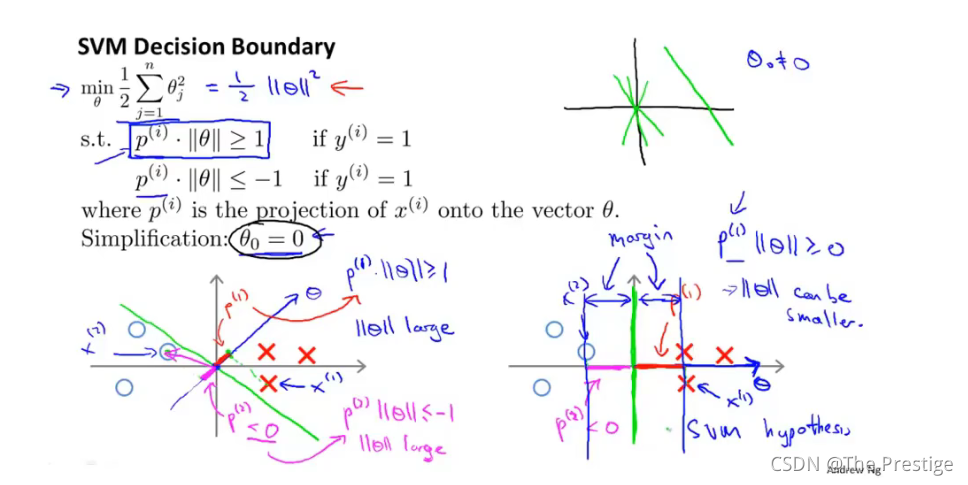
12-4 Kernels I

核函数

Non-linear Decision Boundary

predict y=1 if $${\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1{x}_2+{\theta }_4{x}_1^2+{\theta }_5{x}_2^2+?\ge 0$$

$h_{\theta }(x)=\{\begin{array}{l}1if{\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1{x}_2+?\ge 0\\ 0otherwise\end{array}$

Given x,compute new feature depending on proximity to landmarks $l^{(1)},l^{(2)},l^{(3)}$

Kernels and Similarity

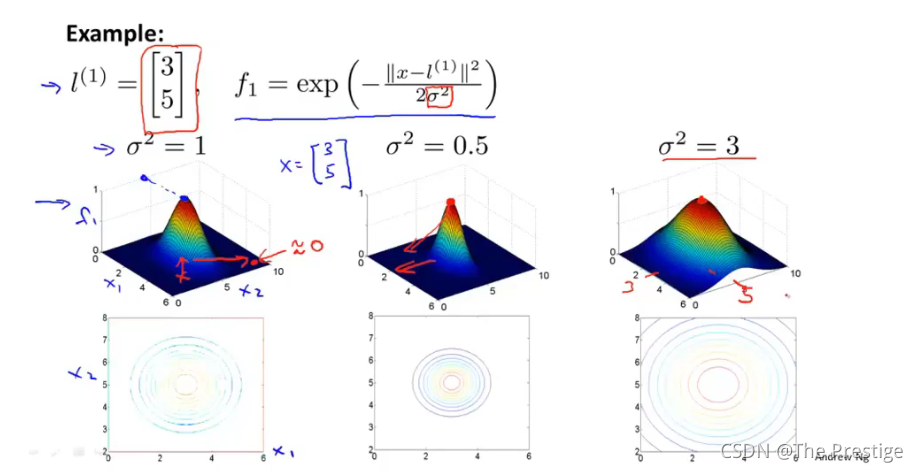
$f_1=similarity(x,l^{(1)})=exp(?\frac{||x?l^{(1)}|{|}^2}{2{\sigma }^2})=\exp (?\frac{{\sum }_{j=1}^n(x_j?l_j^{(1)}{)}^2}{2{\sigma }^2})$

$Ifx\approx l^{(1)}:$$f_1\approx 1$

$Ifxiffarfrom{l}^{(1)}:$$f_1\approx 0$

12-5 Kernels II

Choosing the landmarks

SVM with Kernels

Given $$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),?,(x^{(m)},y^{(m)})$$

choose $$l^{(1)}=x^{(1)},l^{(2)}=x^{(2)},?,l^{(m)}=x^{(m)}$$

Given example x:

? $\begin{array}{l}{f}_1=similarity(x,l^{(1)})\\ f_2=similarity(x,l^{(2)})\\ ?\end{array}$

For training example $(x^{(i)},y^{(i)})?f^{(i)}$

Hypothesis: Given x,compute features $f\in {\mathbb{R}}^{m+1}$

Predict “y=1” if ${\theta }^{T}f\ge 0$

Training:$mi{n}_{\theta }C{\sum }_{i=1}^m[y^{(i)}{cost}_1({\theta }^T{f}^{(i)})+(1?y^{(i)}){cost}_0({\theta }^T{f}^{(i)})]+\frac{1}{2}{\sum }_{i=1}^n{\theta }_j^2$

SVM parameters:

$C(=\frac{1}{\lambda })$.

Large C: Lower bias, high variance.(small $\lambda$)
Small C: Higher bias, low variance.($large\lambda$)

${\sigma }^2$

Large ${\sigma }^2$: Features $f_i$; vary more smoothly. Higher bias, lower variance.

Small ${\sigma }^2$: Features $f_i$; vary less smoothly. Lower bias, Higher variance.

12-6 Using an SVM

Use SVM software package (e.g. liblinear, libsvm, …) to solve for parameters $\theta$

Need to specify:

Choice of parameter C

Choice of kernel (similarity function):

? E.g. No kernel (“linear kernel”)

${\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3+?\ge 0?nlarge,msmall$

? predict:“y=1” if ${\theta }^{T}x\ge 0$

? Gaussian kernel:

$f_i=exp(?\frac{||x?l^{(i)}|{|}^2}{2{\sigma }^2}),where{l}^{(i)}=x^{(i)}$

? Need to choose ${\sigma }^2$

Kernel (similarity) functions:

function f= kernel(x1,x2)
	f=exp((-abs(x1-x2)^2)/(2*(sigma^2)))
return

Note: Do perform feature scaling before using the Gaussian kernel

=[](#4-3 Gradient descent in practice I: Feature Scaling)

Other choices of kernel

Note: Not all similarity functions similarity(x, l) make valid kernels (Need to satisfy technical condition called"mercer’s Theorem"to make sure SVM packages’ optimizations run correctly, and do not diverge)

Many of-the-shelf kernels avaliable:

• Polynomial kernel:$k(x,l)=(x^{T}l{)}^2,(x^{T}l+1{)}^3,(x^{T}l+5{)}^4$
• More esoteric: String kernel, chi-square kernel, histogram intersection kernel

Multi-class classification

Logistic regression vs. SVMS

m=number of features($x\in {\mathbb{R}}^{n+1}$), m =number of training examples
If n is large(relative to m)
Use logistic regression, or SVM without a kernel (“linear kernel”)

If n is small, m is intermediate:
Use SVM with Gaussian kernel

If m is small, m is large:
Create/add more features, then use logistic regression or SVM without a kernel

Neural network likely to work well for most of these settings, but may be slower to train