遗传算法是优化类问题的经典智能算法。本篇将介绍遗传算法的基本概念以及利用遗传算法来求解单目标规划模型。
达尔文进化论的基本思想
遗传算法的设计是受到达尔文进化论的启发。先看下面这张图的几个基本概念。
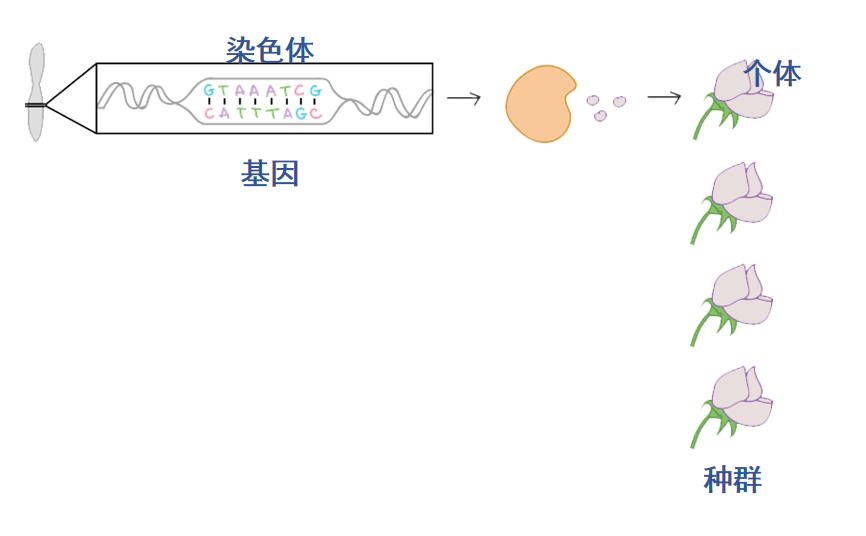
一些花构成一个种群。
每朵花被称为个体。
每个个体内有染色体,染色体上有基因。
通过自然选择,种群内最适合环境的花朵将有更大的概率生存下来,适合环境的程度称作适应度,适应度低的个体将在进化中不断淘汰。
遗传算法的步骤
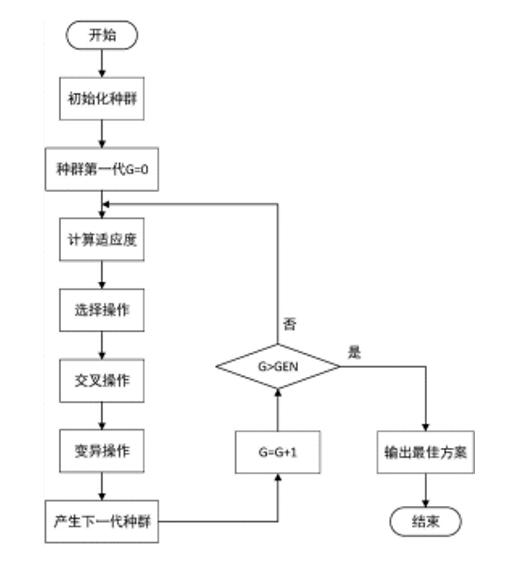
初始化种群
生成固定数量的个体构成种群,每个个体的基因随机赋值。
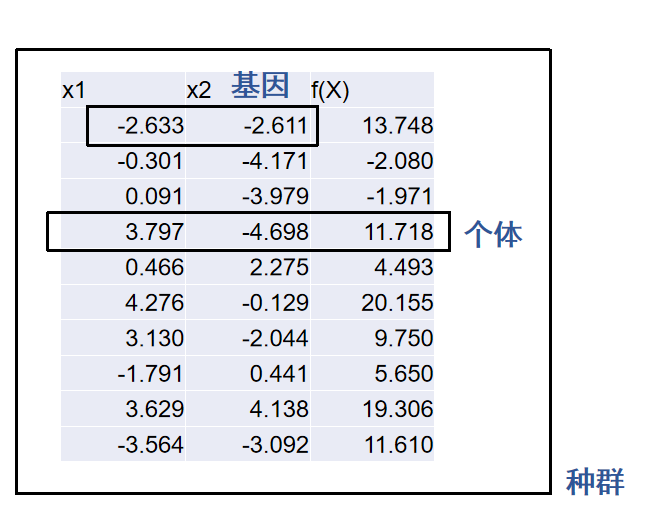
选择操作
选择操作:从旧个体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代。
通过轮盘赌的方法来进行选择。
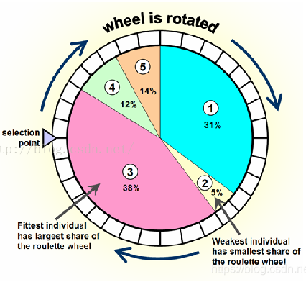
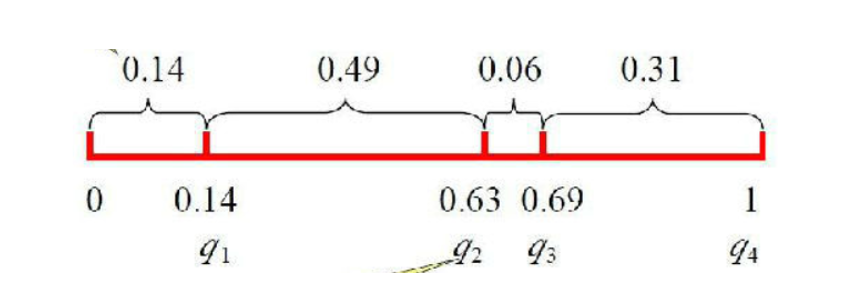
个体适应度占总体适应度的概率,就是该个体被选择的概率。

交叉操作
交叉操作:从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。
采用实数交叉,第k个染色体ak和第l个染色体al在j位的交叉操作方法为,b为[0, 1]随机数:
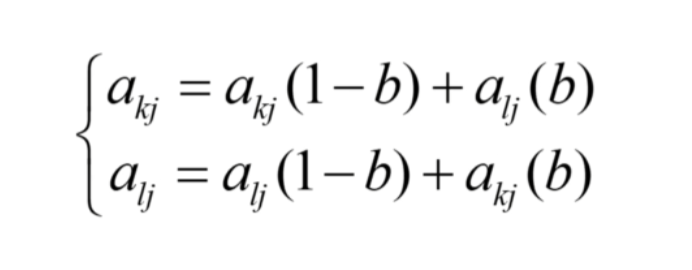
变异操作
变异操作:从种群中随机选择一个个体,选择个体中的一点进行变异以产生更优秀的个体。
第i个个体的第j个基因aij进行变异操作的方法为,r为[0,1]随机数,gen为当前迭代次数,genmax为最大迭代次数:
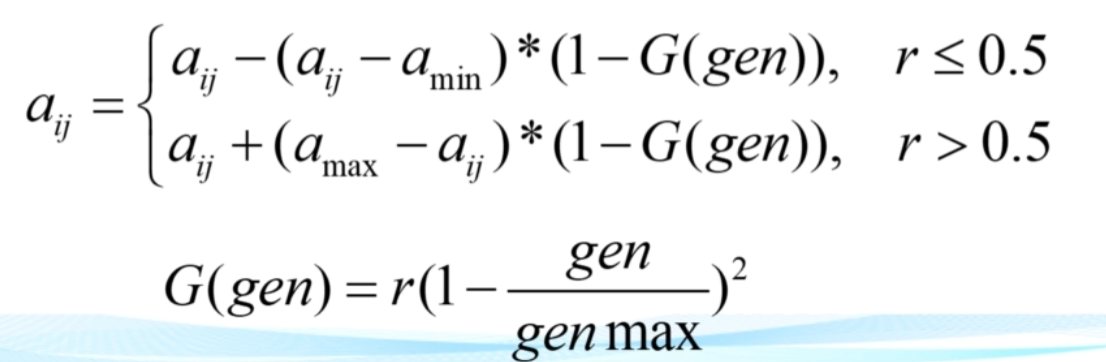
注:交叉操作和编译操作的公式不唯一,主要是这种思想,这里仅为一种可行的函数表示方法。
matlab实现遗传算法
例题 MCM2020B

文件结构
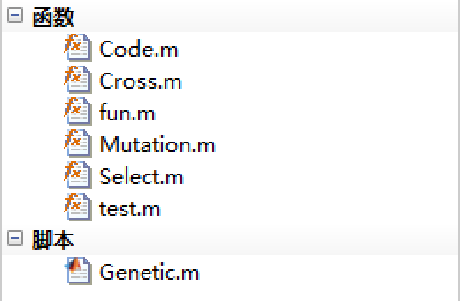
目标函数fun.m
function y = fun(x)
y = 1 / (62.17 * x(2) * sqrt(2 * x(2) * x(1) * sqrt(x(3))) * exp(x(4)));
Sdown = (sqrt(3) / 4) * x(1) ^ 2 * 6;
Sup = x(3) * Sdown;
V = (1 / 3) * x(2) * (Sup + Sdown + sqrt(Sup * Sdown));
if V <= 1 && V >= 0.01
y = y;
else
y = y + 10000;
end
生成随机数 Code.m
function y = fun(x)
y = 1 / (62.17 * x(2) * sqrt(2 * x(2) * x(1) * sqrt(x(3))) * exp(x(4)));
Sdown = (sqrt(3) / 4) * x(1) ^ 2 * 6;
Sup = x(3) * Sdown;
V = (1 / 3) * x(2) * (Sup + Sdown + sqrt(Sup * Sdown));
if V <= 1 && V >= 0.01
y = y;
else
y = y + 10000;
end
判断是否超出边界 test.m
function flag = test(lenchrom, bound, code)
flag = 1;
[n, ~] = size(code);
for i = 1 : n
if code(i) < bound(i, 1) || code(i) > bound(i, 2)
flag = 0;
end
end
选择操作Select.m
function ret = Select(individuals, sizepop)
individuals.fitness = 1 ./ (individuals.fitness);
sumfitness = sum(individuals.fitness);
sumf = individuals.fitness ./ sumfitness;
index=[];
for i = 1 : sizepop
pick = rand;
while pick==0
pick = rand;
end
for j = 1 : sizepop
pick = pick - sumf(j);
if pick < 0
index = [index, j];
break;
end
end
end
individuals.chrom = individuals.chrom(index, :);
individuals.fitness = 1 ./ individuals.fitness(index);
ret = individuals;
交叉操作Cross.m
function ret = Cross(pcross, lenchrom, chrom, sizepop, bound)
for i = 1 : sizepop
pick = rand(1, 2);
while prod(pick) == 0
pick = rand(1, 2);
end
index = ceil(pick .* sizepop);
pick = rand;
while pick == 0
pick = rand;
end
if pick > pcross
continue;
end
flag = 0;
while flag == 0
pick = rand;
while pick == 0
pick = rand;
end
pos = ceil(pick .* sum(lenchrom));
pick = rand;
v1 = chrom(index(1), pos);
v2 = chrom(index(2), pos);
chrom(index(1), pos) = pick * v2 + (1 - pick) * v1;
chrom(index(2), pos) = pick * v1 + (1 - pick) * v2;
flag1 = test(lenchrom, bound, chrom(index(1), :));
flag2 = test(lenchrom, bound, chrom(index(2), :));
if flag1 * flag2 == 0
flag = 0;
else
flag = 1;
end
end
end
ret = chrom;
变异操作Mutation.m
function ret = Mutation(pmutation, lenchrom, chrom, sizepop, pop, bound)
for i = 1 : sizepop
pick = rand;
while pick == 0
pick=rand;
end
index = ceil(pick * sizepop);
pick = rand;
if pick > pmutation
continue;
end
flag = 0;
while flag == 0
pick = rand;
while pick == 0
pick = rand;
end
pos = ceil(pick * sum(lenchrom));
v = chrom(i, pos);
v1 = v - bound(pos, 1);
v2 = bound(pos, 2) - v;
pick = rand;
if pick > 0.5
delta = v2 * (1 - pick ^ ((1 - pop(1) / pop(2)) ^ 2));
chrom(i, pos) = v + delta;
else
delta=v1 * (1 - pick ^ ((1 - pop(1) / pop(2)) ^ 2));
chrom(i, pos) = v - delta;
end
flag = test(lenchrom, bound, chrom(i, :));
end
end
ret = chrom;
主函数Genetic.m
clc
clear
maxgen = 500;
sizepop = 500;
pcross = 0.6;
pmutation = 0.01;
lenchrom = [1, 1, 1, 1]; %这里修改变量个数
bound = [0.2, 0.8; 0.1, 0.6; 0.01, 1; 0.01, 0.25]; %这里修改变量约束范围
individuals = struct('fitness', zeros(1, sizepop), 'chrom', []);
avgfitness = [];
bestfitness = [];
bestchrom = [];
for i = 1 : sizepop
individuals.chrom(i,:) = Code(lenchrom, bound);
x = individuals.chrom(i, :);
individuals.fitness(i) = fun(x);
end
[bestfitness, bestindex] = min(individuals.fitness);
bestchrom = individuals.chrom(bestindex, :);
avgfitness = sum(individuals.fitness) / sizepop;
trace=[];
for i = 1 : maxgen
individuals = Select(individuals, sizepop);
avgfitness = sum(individuals.fitness) / sizepop;
individuals.chrom = Cross(pcross, lenchrom, individuals.chrom, sizepop, bound);
individuals.chrom = Mutation(pmutation, lenchrom, individuals.chrom, sizepop, [i, maxgen], bound);
for j = 1 : sizepop
x = individuals.chrom(j, :);
individuals.fitness(j) = fun(x);
end
[newbestfitness, newbestindex] = min(individuals.fitness);
[worestfitness, worestindex] = max(individuals.fitness);
if bestfitness > newbestfitness
bestfitness = newbestfitness;
bestchrom = individuals.chrom(newbestindex, :);
end
individuals.chrom(worestindex, :) = bestchrom;
individuals.fitness(worestindex) = bestfitness;
avgfitness=sum(individuals.fitness) / sizepop;
trace = [trace; avgfitness, bestfitness];
end
figure
plot((1 : maxgen)', trace(:, 1), 'r-', (1: maxgen)', trace(:, 2), 'b--');
title(['函数值曲线 ' '终止代数=' num2str(maxgen)], 'fontsize', 12);
xlabel('进化代数', 'fontsize', 12);
ylabel('函数值', 'fontsize', 12);
legend('各代平均值', '各代最佳值', 'fontsize', 12);
ylim([-0.5, 5])
disp('函数值 变量');
disp([1 / bestfitness, x]);
实际使用
实际运用时,只需修改目标函数、变量个数及约束条件。
