导语
现如今随着大数据时代的到来,加速了人工智能领域的发展,而现在人工智能最主流的方式就是深度学习,虽然现在有很多深度学习框架 TensorFlow、PyTorch、Keras等等,但是真正掌握到深度学习的核心知识不是仅仅是学会怎样使用框架,而是更应该了解框架背后的源码以及搭建框架的整个思维过程,这样在以后又有新的技术或是当前框架的更新迭代才可以更好的适应新的发展。
——
毕竟人工智能在当代属于前沿技术,那么也就是说还有很多待完善的地方,随着时代的不断发展,当前技术也会不断的更新,有些知识会被淘汰甚至原本对的会变成错的。那么我们就要通过学习了解人工智能发展中始终不变的思维,以及不同时代的主要方法,去了解每一种方法的特性以及有点和在当下的局限性。正如霍金所说,我们在做的是不断推翻前人的工作。只有具备足够的知识储备才能够去深入去推翻。
所以从底层入手,手撸一遍代码。
从0开始
我大概会分为3-5篇来写,过程可能不会很详细,但是会从最基本的开始,那么还是会用波士顿房价作为案例来讲解其中的一些部分。实际上呢我的一个学习笔记的整理,如果有什么错误的话或者有补充的部分也欢迎大家私信我纠正或是交流讨论。
引例
在我们的科学研究和科学活动当中,基本上可以分为三类问题
- 描述性
- 因果推理
- 未来预测
而我们在做的工作就是通过当前的数据情况,去归纳统计出一个规律或模型,然后通过模型作为判断未知情况的依据。也就是说我们所作的工作可以归类为未来预测类。
案例
用波士顿房价预测为例,我们是通过当前的一些数据和房价,进行规律统计和模型训练,进而的得出对未知房价的预测。
(这里代码我就直接贴图了,如果有想要代码的同学可以在我之前的文章中找到波士顿房价预测的代码案例)
- 开始还是现进行数据导入和数据分析
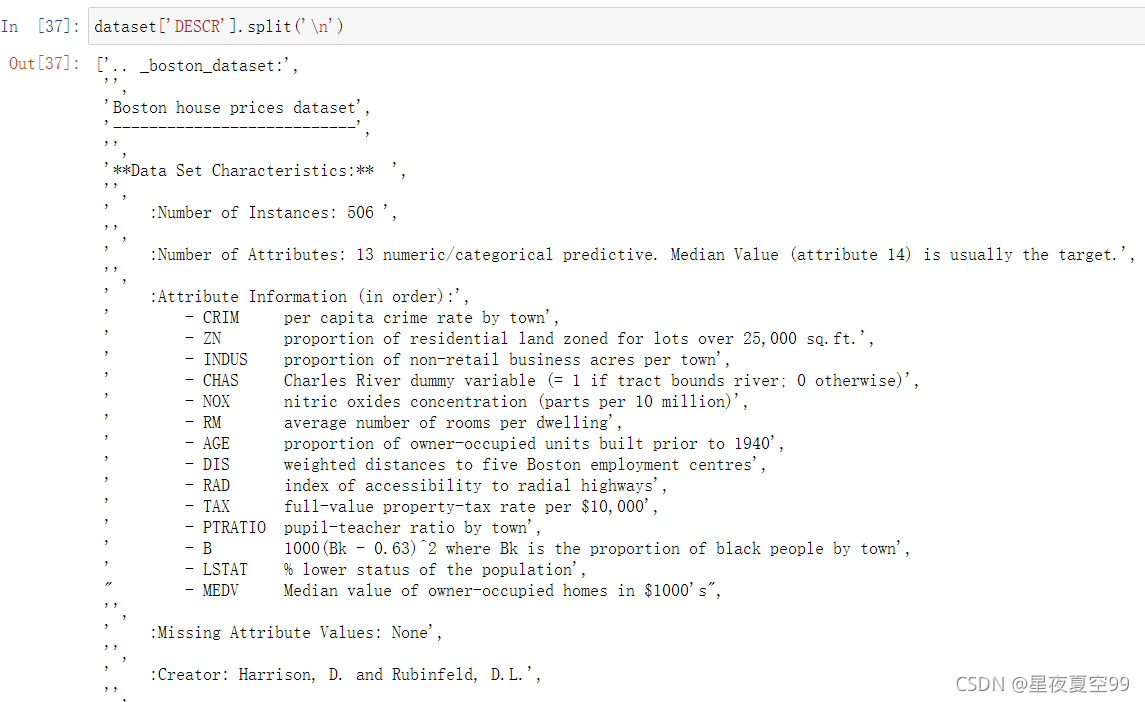
然后根据我们的实际应用情况假设一个场景,假设现在你我就是销售,那么我们就要根据顾客所提出的要求,给出一个波士顿地区大致的房价。为了先简化一下问题我们就先使用RM这个参数或者书影响因素,因为可以从下图中可以看到RM(也就是卧室数量)与价格正相关性最大,所以就先使用RM。实际上这也是特征工程中很重要的一项工作,找到重要特征,RM就是一个重要特征。
下图是表示各个特征与价格的相关性,关于相关性的概念可以在《概率论与数理统计》中协方差那一节找到
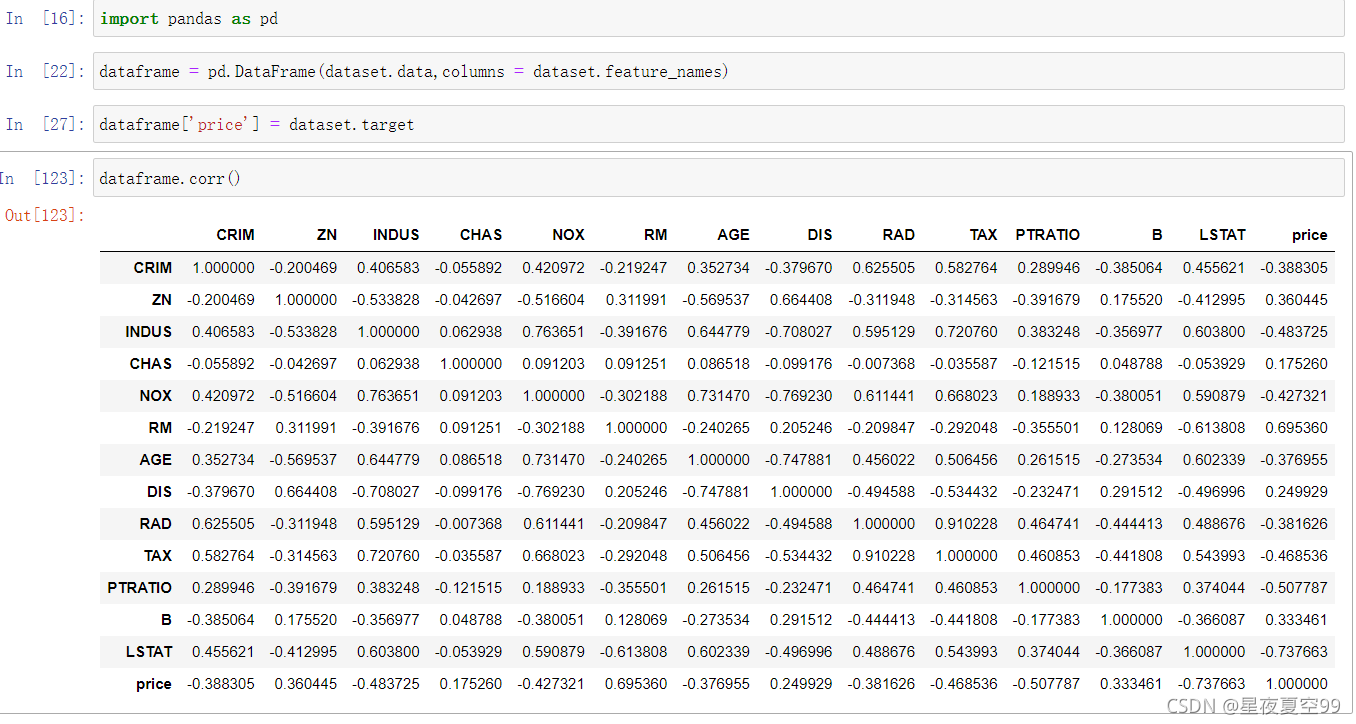
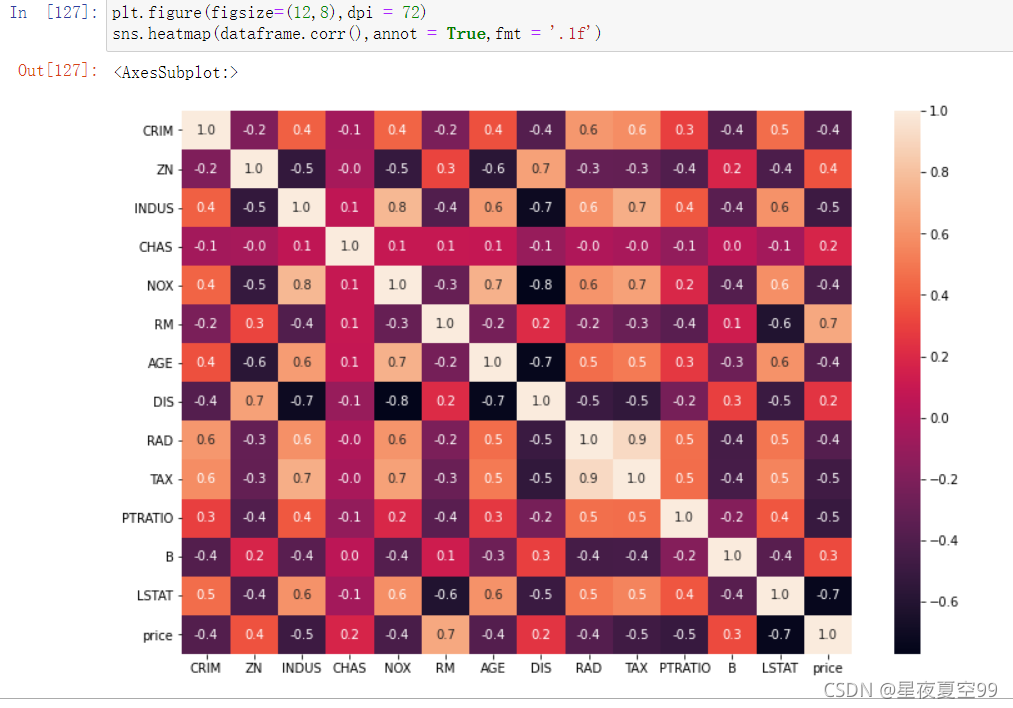
预测方法
现在通过数据我们已经知道RM是影响最大的因素,那么简化问题,我们就假设价格只与RM有关,那么我们应该怎么去预测价格呢???
方法一:KNN
首先,当我们卖房有人咨询的时候,客户给出了一个要求,我们首先要做的是,先去检查已有的案例中是否存在,也就是查询工作。无疑转化为哈希表的形式(python中的字典),查询的速度是最快的。
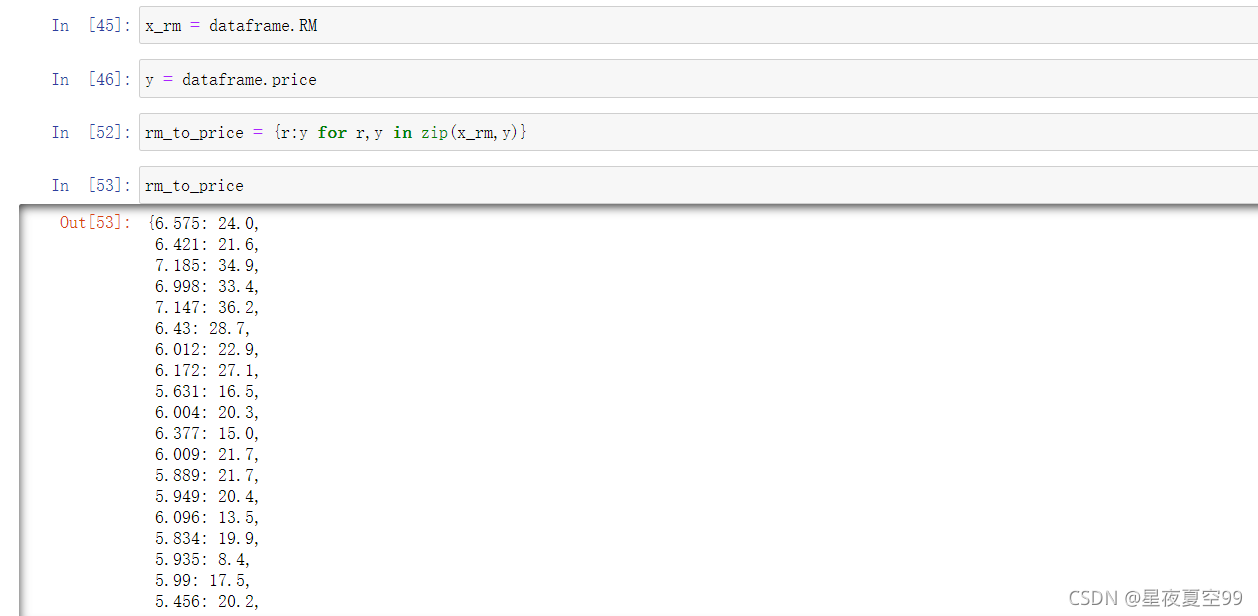
但是呢随着我们卖房的数量越来越多,咨询的人也就越来越多,有一些人问到的情况可能是在我们所查询的表中没有的,那么这个时候我就需要给出一个大致的价格。
当我们用查阅的方法找不到结果时就用临近的数据来进行预估是最方便的。比如说7个卧室是40W,9个卧室是45W,那么8个卧室就是40W-45W那么取平均就是42.5W。代码部分展示如下

这里简单解释一下代码,含义是取query_x附近最近的三个点的平均数。
# 这里我创建一个字典举例
person_and_age = {
'jill' : 24,
'pansy': 30,
'heath': 21,
'jan' : 26,
'dan' : 24,
'crise': 41
}
sorted(person_and_age.items(), key = lambda e:e[1])
#代表根据值来排序
>>>[('heath', 21),
('jill', 24),
('dan', 24),
('jan', 26),
('pansy', 30),
('crise', 41)]
sorted(person_and_age.items(), key = lambda e:(e[1]-25)**2)
#代表距离年龄25最近的值排序,也可以用abs()函数代替 **2 效果是一样,都是为了取正数
>>>[('jill', 24),
('jan', 26),
('dan', 24),
('heath', 21),
('pansy', 30),
('crise', 41)]
np.mean([p for x, p in sorted(history_price.items(), key = lambda x_y:(x_y[0] - query_x)**2)[:3]])
# 该式含义就是选取距离query_x最近的3个数取平均值
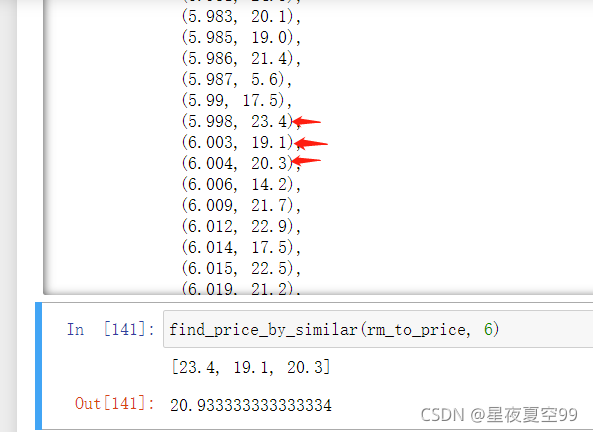
可以看到我要预测6卧室数量的价格,但是表中没有,就选取距离6最近的三个值取平均价格最后得出的结果
那么这个就是KNN(K-Neighbor-Nearest )算法也叫做K近邻,可以发现不论是在理解还是实现又或者结果的预测情况其实都是比较好的一个算法。但是呢他的一个弊端就是当数据量非常庞大的时候,运行速度非常慢,而且KNN只是对于数据中边界内的预测效果比较好,对于边界外的效果就可能会远远偏离实际值。
方法二
KNN的主要问题是速度,那么我们能不能去找到一个方法或者是一个模板,只要给出数据就可以马上反馈结果,其实不难想到,这就是一种映射关系,那么思路就是取拟合一个函数,只要知道系数是什么,输入x就可以得到我们所需的y。
因为x与y的相关系数比较接近于1 ,我们可以设函数 y = kx - b来拟合
那么如何得到最优的k 和 b就是接下来的问题
l
o
s
s
=
1
n
∑
i
∈
N
(
y
i
?
y
i
^
)
2
loss = \frac{1}{n} {\sum_{i \in N}(y_i - \hat{y_i})^2}
loss=n1?i∈N∑?(yi??yi?^?)2
y
^
代
表
的
是
预
测
值
,
y
是
实
际
值
\hat y代表的是预测值,y是实际值
y^?代表的是预测值,y是实际值(在统计学中通常会在预测变量上加 ^ 来表示)
设置一个loss函数,当实际值减去估计值等于0时就说明我们拟合的模型达到了最好的效果,当然达到0几乎时不可能的,所以loss值越小越好
所以说Loss()函数就可以当作我们检验模型可靠性的一个标准
当我们有了参照标准之后,计算k,b就相对简单了
1. 直接使用微积分来计算
y
^
=
k
^
x
+
b
^
\hat y = \hat k x + \hat b
y^?=k^x+b^
l
o
s
s
=
1
n
∑
i
∈
N
(
y
i
?
(
k
^
x
i
+
b
^
)
)
2
loss = \frac{1}{n} {\sum_{i \in N}(y_i - (\hat{k}x_i + \hat{b}))^2}
loss=n1?i∈N∑?(yi??(k^xi?+b^))2
=
>
l
o
s
s
a
i
m
=
A
k
2
+
B
k
+
C
=> loss_{aim} = Ak^2 + Bk +C
=>lossaim?=Ak2+Bk+C
如上式过程我们最终可以得到
l
o
s
s
a
i
m
loss_{aim}
lossaim?可以看到这是一个二次函数,那么可以很轻易的通过
?
b
2
a
-\frac{b}{2a}
?2ab? 得到最优k值,然后带入数据就可以得到b。
数学方法固然简单明了,但是我们知道如果函数过于复杂的时候,其实求导就是一个非常困难的过程,甚至于说无法求导。而在我们的实际过程中影响一个结果的因素是多维的,而且远不止简单的线性关系,所以说该方法,其实并不是一个非常合适的方法。
2. 使用随机模拟的方法来求解最优k,b(蒙特卡洛模拟)
import random
var_max,var_min = 100,-100
k,b = random.randint(var_min,var_max), random.randint(var_min,var_max)
min_loss = float('inf')
best_k, best_b = None,None
def model(x, k ,b):
return x * k + b
total_times = 10000
for t in range(total_times):
k, b = random.randint(var_min,var_max), random.randint(var_min,var_max)
loss_ = loss(y,model(x_rm , k ,b))
if loss_< min_loss:
min_loss = loss_
best_k, best_b = k, b
print(f'在{t}时刻找到了更好的k:{best_k} b:{best_b}')
>>>在0时刻找到了更好的k:17 b:67
在1时刻找到了更好的k:4 b:-61
在2时刻找到了更好的k:3 b:-42
在15时刻找到了更好的k:3 b:-31
在63时刻找到了更好的k:7 b:-33
在134时刻找到了更好的k:18 b:-92
在250时刻找到了更好的k:12 b:-48
在499时刻找到了更好的k:4 b:1
在635时刻找到了更好的k:7 b:-18
在774时刻找到了更好的k:13 b:-59
在1772时刻找到了更好的k:7 b:-21
在5629时刻找到了更好的k:9 b:-35
其中的x就是RM,y是price
但是在训练中我们可以发现一个问题就是,随着最优k,b的更新次数增加,找到更好的k,b就需要更长的时间。这需要很多的时间成本,而且更重要的是我们只是相较于之前的模型进行了优化,但是优化了多少我们并不清楚,以及还有进行多少次数,这些都是未知数。简单的理解就是通过计算机帮助我们瞎猜,但是我们却没有一个停止猜的标准,所以说这种方式是很糟糕的一种方式。
3.梯度下降
梯度这个概念大家其实可以在高等数学(下)在方向导数那一节可以找到学习一下,或者可以从B站搜一下吴恩达老师的视频,讲解也是比较详细的。
我简单讲解一下

从方法一可以知道最低点就是最优的k值,所以我们的任务就是无限向最低点逼近如果说我们用当前随机一个点减去它的导数,就会一直向它逼近。
当然也要在导数前加上一个合适系数,不然就会造成下面的效果,不停的震荡。
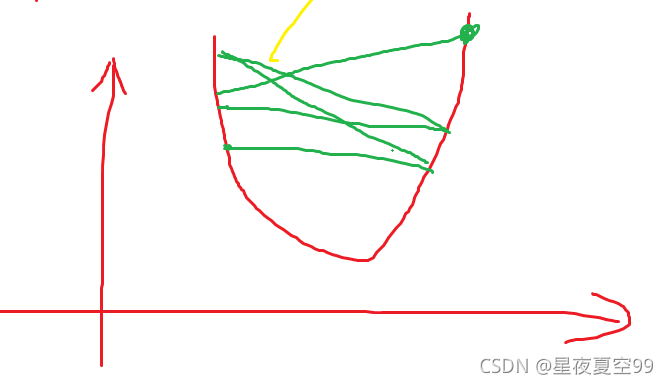
所以表达式为
?
k
n
+
1
=
k
n
+
?
1
?
l
o
s
s
?
k
n
\star{k_{n+1}} = k_n + -1 \frac{ \partial{loss}}{\partial{k_n}}
?kn+1?=kn?+?1?kn??loss?
?
b
n
+
1
=
b
n
+
?
1
?
l
o
s
s
?
b
n
\star{b_{n+1}} = b_n + -1 \frac{ \partial{loss}}{\partial{b_n}}
?bn+1?=bn?+?1?bn??loss?
def loss(y,yhat):
return np.mean((np.array(y) - np.array(yhat)) **2)
def partial_k(x,y,k,b):
return 2 * np.mean((y - (k * x +b)) * (-x))
def partial_b(x,y,k,b):
return 2 * np.mean((y - (k * x +b)) * (-1))
var_max,var_min = 100,-100
k,b = random.randint(var_min,var_max), random.randint(var_min,var_max)
min_loss = float('inf')
best_k, best_b = None,None
total_times = 500
alpha = 1e-4
for t in range(total_times):
k = k + (-1) * partial_k(x_rm,y,k,b) * alpha
b = b + (-1) * partial_k(x_rm,y,k,b) * alpha
loss_ = loss(y, model(x_rm,k,b))
if loss_< min_loss:
min_loss = loss_
best_k, best_b = k, b
print(f'在{t}时刻找到了更好的k:{best_k} b:{best_b}')

可以从运行结果上看每一次的loss值都是在递减的,而且是很明确的是梯度在不断的下降,也就是说在不断的逼近最优值,只要设置合适的学习率以及一个合适标准,我们就可以得到一组比较好的模型。
我们现在用的办法就是叫做梯度下降(Gradien Descent)。使用梯度下降一个好处就是,这种方式是以肉眼可见的方式在不断逼近最优解。
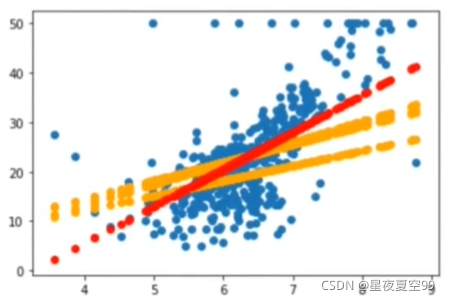
可以看到每次的曲线效果都是在不断变好的
这也是当前深度学习的核心内容,也就是说深度学习做的就是通过梯度下降的方式得到一组最优解。