用`numpy`实现最简单的前馈神经网络——神经网络架构篇

基础知识

梯度（高等数学）、矩阵运算（线性代数）、numpy(ndarray)、python基础语法
目录
1. 神经网络架构
2. 神经网络建立
  
  先用比较简单的正向传播建立好框架，再用反向传播改变算法
3. 实例：学习mnist手写数字数据集

神经网络架构

矩阵
拟合
梯度

矩阵运算

我们可以把矩阵看作一个特殊的函数，它的作用是将长度为n的向量（如下图 $\bold{A}$ ）转化为长度为m的向量（如下图 $\bold{Z}$ ）。

将输入看作一个包含n个元素的向量，就可以通过多次矩阵运算转化为长度为m的输出了。

虽然此时输入矩阵（ $\bold{A}$ ）在变换矩阵（ $\bold{W}$ ）的右侧，但是这是可以改变的，在mnist学习实例中我就会将 $\bold{A}$ 放在 $\bold{W}$ 左侧（当然此时m和n会发生一些变化）。
$\begin{pmatrix} w_{11} & w_{12} & \cdots & w_{1n} \\ w_{21} & w_{22} & \cdots & w_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ w_{m1} & w_{m2} & \cdots & w_{mn} \\ \end{pmatrix} \cdot \begin{bmatrix} a_{1} \\ a_{2} \\ \vdots \\ a_{n} \\ \end{bmatrix} + \begin{pmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{m} \\ \end{pmatrix} = \begin{bmatrix} z_{1} \\ z_{2} \\ \vdots \\ z_{m} \\ \end{bmatrix}$

$\bold{W}_{m \times n} \cdot \bold{A}_n + \bold{B}_m= \bold{Z}_m, \\ F(\bold{A}_n) = \bold{Z}_m.$

在Python中，使用矩阵进行向量化编程也是加快学习速度的必要手段

拟合——深度学习的目的

最简单的拟合——线性回归

我们在中学中曾经学习的用一系列数据对来得出一条线性拟合曲线，还使用了最小二乘法。事实上，深度学习做的也是类似的事情。
$\hat{y} = ax+b.$

深度学习中的拟合

不同的是深度学习中不仅需要线性的拟合，也需要非线性的拟合。（这很正常因为自然界很多事不是线性的）

因此我们需要引入非线性的函数来变换向量，就需要激活函数（下图 $\alpha$ 就是一种激活函数），因为如果只有线性的函数的话，就不可能获得非线性的拟合。

$y^{(i)}=\alpha(x^{(i)}_1 w_1+x^{(i)}_2 w_2 + \dots + x^{(i)}_n w_n + b^{(i)}), \\ \alpha(z) = \frac{1}{1+e^{-z}}.$

$\text{provided f(x) and g(x) is linear,} \\ \text{it's easy to get that f(g(x)) is linear}$

同时我们需要一个标准来衡量拟合的贴合度，就得到了损失函数

均方误差函数
$\ell^{(i)}(a, b) = \frac{1}{2} \left(\hat{y}^{(i)} - y^{(i)}\right)^2, \\ \ell(a, b) =\frac{1}{n} \sum_{i=1}^n \ell^{(i)}(a, b) =\frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(ax^{(i)} + b - y^{(i)}\right)^2.$

交叉熵损失函数
$\ell^{(i)} = \frac{1}{N}L_{(i)}=-\frac{1}{N}\sum_i[y^{(i)} \cdot \log(\hat y^{(i)})+(1-y^{(i)} ) \cdot \log(1-\hat y^{(i)})].$

平均损失最小——梯度下降法

和线性回归中相同，要使拟合最贴合，就是在给定输入（A）时，调整参数（W、B）使损失函数最小。
$w^?_1,w^?_2,\dots,w^*_n,b^?=argmin\{?(w_1,w_2,\dots,w_n,b)\}.$

使用高等数学的知识，要如何使某个函数取得最小值呢？

画图？求极值点再求最小值点？可惜的是这些方法在这里都行不通（想想那复杂的表达式和万亿计的自变量吧）

最小二乘法也是求损失函数最小值的一种方法

因此我们只能退而求其次，求得一个局部最小值，希望也能拟合得不错，这也就是梯度下降法（偏导数求最小值法）。

让自变量不断沿着梯度的反方向移动，就能获得极小值
$f(x,y)=x^2+y^2, \\ (\Delta x, \Delta y) = ?η (\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}).$

在jupyter notebook中运行如下代码

%matplotlib notebook

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

import numpy as np
from pprint import pprint

def f(x, y):
    """待求函数"""
    return x ** 2 + y ** 2

def grad(func, *args):
    """求梯度"""
    h = 1e-6
    args = list(args)
    grad = [None for _ in range(len(args))]
    for i, arg in enumerate(args):
        args[i] = arg + h
        f1 = f(*args)
        args[i] = arg - h
        f2 = f(*args)
        args[i] = arg
        grad[i] = (f1 - f2) / 2 / h
    return grad

fig = plt.figure()
ax = Axes3D(fig)

# 图像范围
a = np.arange(-50, 50, 0.1)
b = np.arange(-50, 50, 0.1)

# 作出完整图像
X, Y = np.meshgrid(a, b)
Z = f(X, Y)

# 记录每一步的x, y, z值
xs = [50]
ys = [43]
zs = [f(xs[-1], ys[-1])]

step_length = 0.03  # 学习率，每一步的步长
step_num = 50 # 学习次数

for _ in range(step_num):
    x = xs[-1]
    y = ys[-1]
    dx, dy = grad(f, x, y)  # 变化量
    x -= dx * step_length
    y -= dy * step_length
    xs.append(x)
    ys.append(y)
    zs.append(f(x, y))

ax.scatter3D(xs, ys, zs, cmap="Blues")  # 散点图
ax.plot_surface(X, Y, Z, cmap="rainbow")  # 三维曲面

pprint(list(zip(xs, ys, zs)))

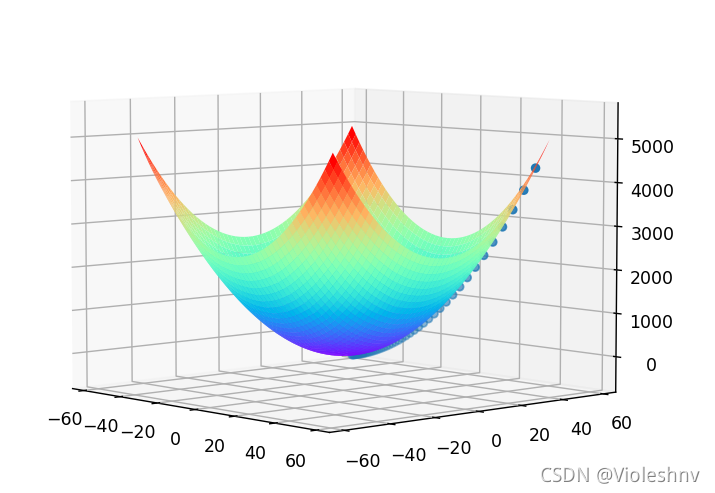
梯度下降法求x^2 + y^2极小值

可以看到蓝点一步步的走向极小值。

当然，局部最小值就是极值点，这种方法有可能会陷入某个极小值，错过了最小值。（可以尝试修改一下代码来看看这种情况，比如更改代求函数和学习率）

反向传播和链式法则

反向传播法其实就是利用链式法则用更快的方法求偏导数。但和正向一样使用梯度下降来求损失函数最小值
$\text{forward propagation: } \Delta x = \frac{?f}{?x} = \lim_{h \to 0} \frac{f(x+h)-f(x-h)}{2h}, \\ \text{back-propagation: } \Delta x = \frac{?f}{?x}=\prod(\frac{?f}{?y},\frac{?y}{?x}).$

激活函数和损失函数的选择

def sigmoid(x):
    """激活函数"""
    return 1 / (1 + np.exp(-x))


def cross_entropy_error(result, labels):
    """损失函数"""
    return -(np.sum(np.log(result[np.arange(labels.size), labels] + 1e-5)))


def soft_max(x):
    """输出函数"""
    t = np.exp(x - x.max())
    y = np.sum(t, axis=1).reshape(t.shape[0], 1)
    return t / y