[人工智能] 线性回归：优化函数(1)—

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 线性回归：优化函数(1)——最小二乘法优化 -> 正文阅读

[人工智能]线性回归：优化函数(1)——最小二乘法优化

最小二乘法（Ordinary Least Square, OLS）是用数学公式直接求解线性回归方程的参数的方法。以最简单的一元线性回归为例，公式6-4中显示一系列的X值可以求出一系列的预测值Y’，的目的是使得每一对预测的Y’和Y之间的误差(Y- Y’)最小化。由于误差有正误差有负误差，为了避免彼此抵消，需要使用误差的平方来衡量。虽然绝对值也可以避免误差抵消，但是绝对值的代数计算性不如平方好，不便于求微分。二乘表示平方，最小二乘法就表示求误差平方和最小的方法。在这里插入图片描述
现在我们来用代码手工的实现出一个线性回归模型按照最小二乘法优化的线性回归方程。

import pandas as pd

# 读取鲍鱼信息
Abalone = pd.read_csv('AbaloneAgePrediction.txt',header=None)

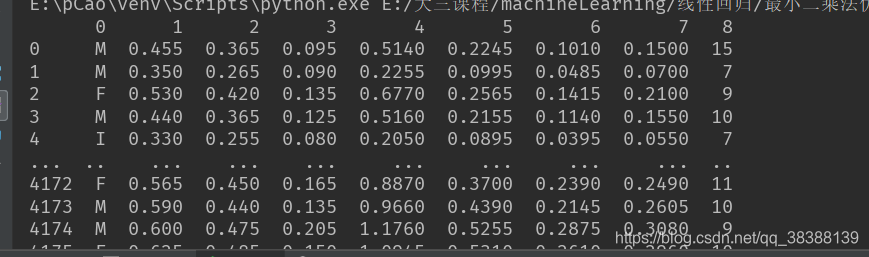
在这里插入图片描述
可以看到他是一个没有列名的DataFrame,根据信息修改他的列名,用.corr()方法查看他的相关度。

Abalone.columns=['Sex', 'Length', 'Diameter', 'Height','Whole weight', 'Shucked weight',
                 'Viscera weight','Shell weight', 'Rings']  # 根据信息修改他的列名

print(Abalone.corr())

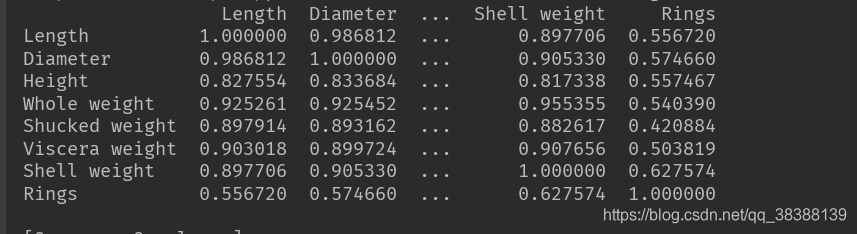
在这里插入图片描述
可以看到Rings和Shell weight的相关度最高。所以我们只取这两列(我们只是想看看最小二乘法的原理,就只取两列来进行验证)

AbaloneRing = Abalone[['Shell weight','Rings']]   # 根据相关性取两列

根据上面的公示图。我们可以知道我们要算的是：
c =（壳重-壳重平均值）*（鲍鱼年龄-鲍鱼年龄平均值）的累加和 /（壳重-壳重平均值）的平方的累加和
b = 鲍鱼年龄平均值-c*壳重的平均值
我们针对这个公式写个函数


def least_square_method(arg,arg2):
    c = ((arg-arg.mean())*(arg2-arg2.mean())).sum()/((arg-arg.mean())**2).sum()
    b = arg2.mean()-c*arg.mean()
    return c,b

使用


c,b=least_square_method(AbaloneRing['Shell weight'],AbaloneRing['Rings'])

print(c,b)

输出
在这里插入图片描述
验证：我们用sklean中的LinearRegression来对该数据进行一个拟合验证


from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(AbaloneRing[['Shell weight']],AbaloneRing['Rings'])  # 数据需要一个（-1，1）形状的数据
print(model.coef_,model.intercept_)   # 输出系数和截距

在这里插入图片描述
这个LinearRegression所使用的优化函数就是最小二乘法优化

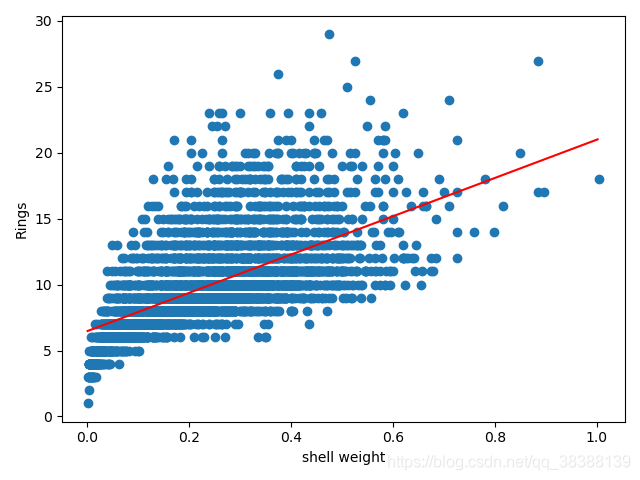
我们可以画图的形式查看这些数据与用最小二乘法公式画出来的线的联系


import numpy as np
import matplotlib.pyplot as plt
x=np.arange(AbaloneRing['Shell weight'].min(),AbaloneRing['Shell weight'].max())
y=x*c+b
plt.scatter(AbaloneRing['Shell weight'],AbaloneRing['Rings'])
plt.plot(np.arange(AbaloneRing['Shell weight'].min(),AbaloneRing['Shell weight'].max()),y,color = 'red')
plt.ylabel('Rings')
plt.xlabel('shell weight')
plt.show()

在这里插入图片描述
这只是一个一元参数的回归模型，如果想构建一个多元参数的线性回归模型。那么就要进行推导了。其实我也不会，但是好在有直接的公式

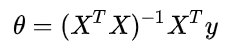
我们只需要把这个公式表达出来就行了

def least_square_method(arg,arg2):
    X = np.hstack([np.ones((len(arg), 1)), arg])

    formula= np.linalg.inv(X.T.dot(X)).dot(X.T).dot(arg2)  # np.linalg.inv 矩阵求逆
    b = formula[0]     # 截距
    c = formula[1:]   # 参数

    return c,b

print(least_square_method(AbaloneRing[['Shell weight','Diameter']],AbaloneRing['Rings']))


from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(AbaloneRing[['Shell weight','Diameter']],AbaloneRing['Rings'])  # 数据需要一个（-1，1）形状的数据
print(model.coef_,model.intercept_)   # 输出系数和截距