一、简介
- 无监督聚类算法的目标是基于表示空间的距离度量来发现数据中的语义类别;
- 近期聚类研究主要集中在将深度学习和聚类集成在一起,这些方法尽管对聚类有所改善,但在具有大量簇的复杂数据上表现仍不尽如人意;主要原因是在聚类开始时,需要不同类别会存在一定的重叠;
- 实例级别的对比学习(Instance-CL)近期在自监督领域实现了巨大的成功。本质上,Instance-CL会在分散不同实例的同时,也隐式地将相似实例聚集在一起。因此,可以利用对比学习的这个性质,将聚类时重叠的样本分开;
- 论文提出了聚类算法 SCCL(Supporting?Clustering?with?Contrastive?Learning) \text{SCCL(Supporting Clustering with Contrastive Learning)} SCCL(Supporting?Clustering?with?Contrastive?Learning),该方法联合优化聚类损失函数和实例级对比学习;
- 论文在短文本聚类上评估了 SCCL \text{SCCL} SCCL,结果显示 SCCL \text{SCCL} SCCL在绝大多数数据集上超过了 SOTA \text{SOTA} SOTA方法,准确率上升3%-11%,归一化互信息上升4%-15%;
二、算法 SCCL \text{SCCL} SCCL
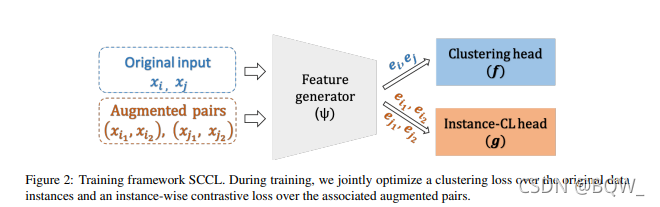
? 论文的目标是开发一个能够利用Instance-CL优点的聚类算法。下图是 SCCL \text{SCCL} SCCL的整体框架,由三个部分组成。其中一个神经网络 ψ ( ? ) \psi(\cdot) ψ(?)负责将输入数据映射至表示空间,然后跟两个不同的头 g ( ? ) g(\cdot) g(?)和 f ( ? ) f(\cdot) f(?),分别用于对比损失函数和聚类损失函数。
? 模型的数据是由原始数据和增强数据组成。具体来说,对于随机采样的一个batch B = { x i } i = 1 M \mathcal{B}=\{x_i\}_{i=1}^M B={xi?}i=1M?,为 B \mathcal{B} B中的每一个实例生成一对增强数据。最终返回一个增强batch B a \mathcal{B}^a Ba,大小为 B a \mathcal{B}^a Ba,即 B a = { x ~ i } i = 1 2 M \mathcal{B}^a=\{\tilde{x}_i\}_{i=1}^{2M} Ba={x~i?}i=12M?。
2.1 实例级对比学习
? i 1 ∈ { 1 , … , 2 M } i^1\in\{1,\dots,2M\} i1∈{1,…,2M}表示增强数据集 B a \mathcal{B}^a Ba中任意实例, i 2 ∈ { 1 , … , 2 M } i^2\in\{1,\dots,2M\} i2∈{1,…,2M}是增强数据集 B a \mathcal{B}^a Ba中另一个实例,这两个增强实例均来自 B \mathcal{B} B中的同样实例。将 x ~ i 1 , x ~ i 2 ∈ B a \tilde{x}_{i^1},\tilde{x}_{i^2}\in\mathcal{B}^a x~i1?,x~i2?∈Ba作为正实例,将 B a \mathcal{B}^a Ba中的其他 2 M ? 2 2M-2 2M?2样本作为负实例。令 z ~ i 1 \tilde{z}_{i^1} z~i1?和 z ~ i 2 \tilde{z}_{i^2} z~i2?为头 g g g对应的输出,即 z ~ j = g ( ψ ( x ~ j ) ) , j = i 1 , i 2 \tilde{z}_j=g(\psi(\tilde{x}_j)),j=i^1,i^2 z~j?=g(ψ(x~j?)),j=i1,i2。
? 通过下面的损失函数拉近
x
~
i
1
\tilde{x}_{i^1}
x~i1?和
x
~
i
2
\tilde{x}_{i^2}
x~i2?的距离,并拉远与
B
a
\mathcal{B}^a
Ba中其他样本间的距离。
l
i
1
I
=
?
l
o
g
exp
(
sim
(
z
~
i
1
,
z
~
i
2
/
τ
)
)
∑
j
=
1
2
M
1
j
≠
i
1
?
exp(sim(
z
~
i
1
,
z
~
j
)
/
τ
)
l_{i^1}^I=-log\frac{\text{exp}(\text{sim}(\tilde{z}_{i^1},\tilde{z}_{i^2}/\tau))}{\sum_{j=1}^{2M}\mathbb{1}_{j\neq i^1}\cdot \text{exp(sim(}\tilde{z}_{i^1},\tilde{z}_{j})/\tau)}
li1I?=?log∑j=12M?1j?=i1??exp(sim(z~i1?,z~j?)/τ)exp(sim(z~i1?,z~i2?/τ))?
其中,
1
j
≠
i
1
\mathbb{1}_{j\neq i^1}
1j?=i1?是一个indicator函数且
τ
\tau
τ为温度参数,论文设置为0.5。相似函数
sim
(
?
)
\text{sim}(\cdot)
sim(?)选择正则化向量的点积,即
sim
(
z
~
i
,
z
~
j
)
=
z
~
i
T
z
~
j
/
∣
∣
z
~
i
∣
∣
2
∣
∣
z
~
j
∣
∣
2
\text{sim}(\tilde{z}_i,\tilde{z}_j)=\tilde{z}_i^T\tilde{z}_j/||\tilde{z}_i||_2||\tilde{z}_j||_2
sim(z~i?,z~j?)=z~iT?z~j?/∣∣z~i?∣∣2?∣∣z~j?∣∣2?。
? 实例级对比学习在整个数据集
B
a
\mathcal{B}^a
Ba的平均为
L
Instance-CL
=
1
2
M
∑
i
=
1
2
M
l
i
I
\mathcal{L}_{\text{Instance-CL}}=\frac{1}{2M}\sum_{i=1}^{2M}l_i^I
LInstance-CL?=2M1?i=1∑2M?liI?
2.2 聚类
聚类这部分的算法主要来自于论文《Unsupervised Deep Embedding for Clustering Analysis》,可以参考该博客。
? 不同于实例级对比学习,聚类专注在高级语义概念并参数将相似语义概念的实例聚在同一个类别。假设数据有
K
K
K个语义类别,每个类别使用表示空间的中心点特征向量来表示,簇中心
u
k
,
k
∈
{
1
,
…
,
K
}
u_k,k\in\{1,\dots,K\}
uk?,k∈{1,…,K}。令
e
j
=
ψ
(
x
j
)
e_j=\psi(x_j)
ej?=ψ(xj?)表示原始数据集
B
\mathcal{B}
B中实例
x
j
x_j
xj?的向量表示。这里使用学习
t
t
t分布来来计算将
x
j
x_j
xj?分配值
k
t
h
k^{th}
kth簇的概率
q
j
k
=
(
1
+
∣
∣
e
j
?
u
k
∣
∣
2
2
/
α
)
?
α
+
1
2
∑
k
′
=
1
K
(
1
+
∣
∣
e
j
?
u
k
′
∣
∣
2
2
/
α
)
?
α
+
1
2
q_{jk}=\frac{(1+||e_j-u_k||_2^2/\alpha)^{-\frac{\alpha+1}{2}}}{\sum_{k'=1}^K(1+||e_j-u_{k'}||_2^2/\alpha)^{-\frac{\alpha+1}{2}}}
qjk?=∑k′=1K?(1+∣∣ej??uk′?∣∣22?/α)?2α+1?(1+∣∣ej??uk?∣∣22?/α)?2α+1??
其中,
α
\alpha
α表示学生
t
t
t分布的自由度。在没有明确提及的情况下,将设置
α
=
1
\alpha=1
α=1。
? 这里使用线性层(聚类头)来近似每个簇的中心点,并利用一个辅助分布来迭代改进聚类效果。具体来说,令
p
j
k
p_{jk}
pjk?来表示辅助概率分布,定义为
p
j
k
=
q
j
k
2
/
f
k
∑
k
′
q
j
k
2
/
f
k
′
p_{jk}=\frac{q_{jk}^2/f_k}{\sum_{k'}q_{jk}^2/f_{k'}}
pjk?=∑k′?qjk2?/fk′?qjk2?/fk??
其中,
f
k
=
∑
j
=
1
M
q
j
k
,
k
=
1
,
…
,
K
f_k=\sum_{j=1}^M q_{jk},k=1,\dots,K
fk?=∑j=1M?qjk?,k=1,…,K是一个batch中的软聚类频率。这个辅助分布鼓励学习高置信度分数并同时克服不平衡簇带来的偏差。
? 最终,通过KL散度来拉近分配概率和目标分布的距离
l
j
C
=
KL
[
p
j
∣
∣
q
j
]
=
∑
k
=
1
K
p
j
k
log
p
j
k
q
j
k
l_j^C=\text{KL}[p_j||q_j]=\sum_{k=1}^Kp_{jk}\text{log}\frac{p_{jk}}{q_{jk}}
ljC?=KL[pj?∣∣qj?]=k=1∑K?pjk?logqjk?pjk??
? 整个batch上的损失函数为
L
Cluster
=
∑
j
=
1
M
l
j
C
/
M
\mathcal{L}_{\text{Cluster}}=\sum_{j=1}^M l_j^C/M
LCluster?=j=1∑M?ljC?/M
2.3 联合损失函数
? 整个
SCCL
\text{SCCL}
SCCL的损失函数为
L
=
L
Instance-CL
+
L
Cluster
=
∑
j
=
1
M
l
j
C
/
M
+
η
∑
i
=
1
2
M
l
i
I
/
2
M
\begin{aligned} \mathcal{L}&=\mathcal{L}_{\text{Instance-CL}}+\mathcal{L}_{\text{Cluster}}\\ &=\sum_{j=1}^M l_j^C/M+\eta\sum_{i=1}^{2M}l_i^I/2M \end{aligned}
L?=LInstance-CL?+LCluster?=j=1∑M?ljC?/M+ηi=1∑2M?liI?/2M?
其中,
l
i
C
l_i^C
liC?和
l
i
I
l_i^I
liI?在上面定义。
η
\eta
η用来平衡两种Loss,其被设置为10。需要注意的是,聚类损失函数仅在原始数据上被优化。此外,我们也可以利用增强数据来增强每个实体的聚类一致性。