[人工智能]机器学习算法基础——朴素贝叶斯算法

26.朴素贝叶斯算法原理

联合概率和条件概率

联合概率：包含多个条件，且所有条件同时成立的概率 记作：P(A,B)

• P(A,B)=P(A)P(B)

条件概率：就是事件A在另外一个事件B已经发生条件下的发生概率 记作：P(A|B)

• 特性：P(A1,A2|B) = P(A1|B)P(A2|B)
• 注意：此条件概率的成立，是由于A1,A2相互独立的结果

朴素贝叶斯-贝叶斯公式?

?sklearn朴素贝叶斯实现API

sklearn.naive_bayes.MultinomialNB(alpha = 1.0)

• alpha：拉普拉斯平滑系数

27.朴素贝叶斯算法对新闻进行分类案例

sklearn20类新闻分类

20个新闻组数据集包含20个主题的18000个新闻组帖子

from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
def naivebayes():
    news = fetch_20newsgroups(subset="all")
    #进行数据分割
    x_train, x_test, y_train, y_test = train_test_split(news.data,news.target,test_size=0.25)
    #对数据集进行特征抽取
    tf = TfidfVectorizer()
    # 以训练集当中的词的列表进行每篇文章重要性统计
    x_train = tf.fit_transform(x_train)
    print(tf.get_feature_names())
    x_test = tf.transform(x_test)
    #进行朴素贝叶斯算法
    mlt = MultinomialNB(alpha=1.0)
    print(x_train.toarray())

    mlt.fit(x_train,y_train)

    y_predict = mlt.predict(x_test)
    print("预测的文章类别为:",y_predict)
    print("准确率为:",mlt.score(x_test,y_test))
    return None
naivebayes()

[[0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 ...
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]
 [0. 0. 0. ... 0. 0. 0.]]
预测的文章类别为: [ 9 10 16 ...  8  8  8]
准确率为: 0.8442275042444821

28.朴素贝叶斯算法总结

朴素贝叶斯分类优缺点

优点：

1. 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
2. 对缺失数据不太敏感，算法也比较简单，常用于文本分类。
3. 分类准确度高,速度快
4. 不需要调参数

缺点：

1. 需要知道先验概率P(F1,F2,…|C)，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

29.精确率和召回率

分类模型的评估

• estimator.score() 一般最常见使用的是准确率，即预测结果正确的百分比

混淆矩阵

在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)

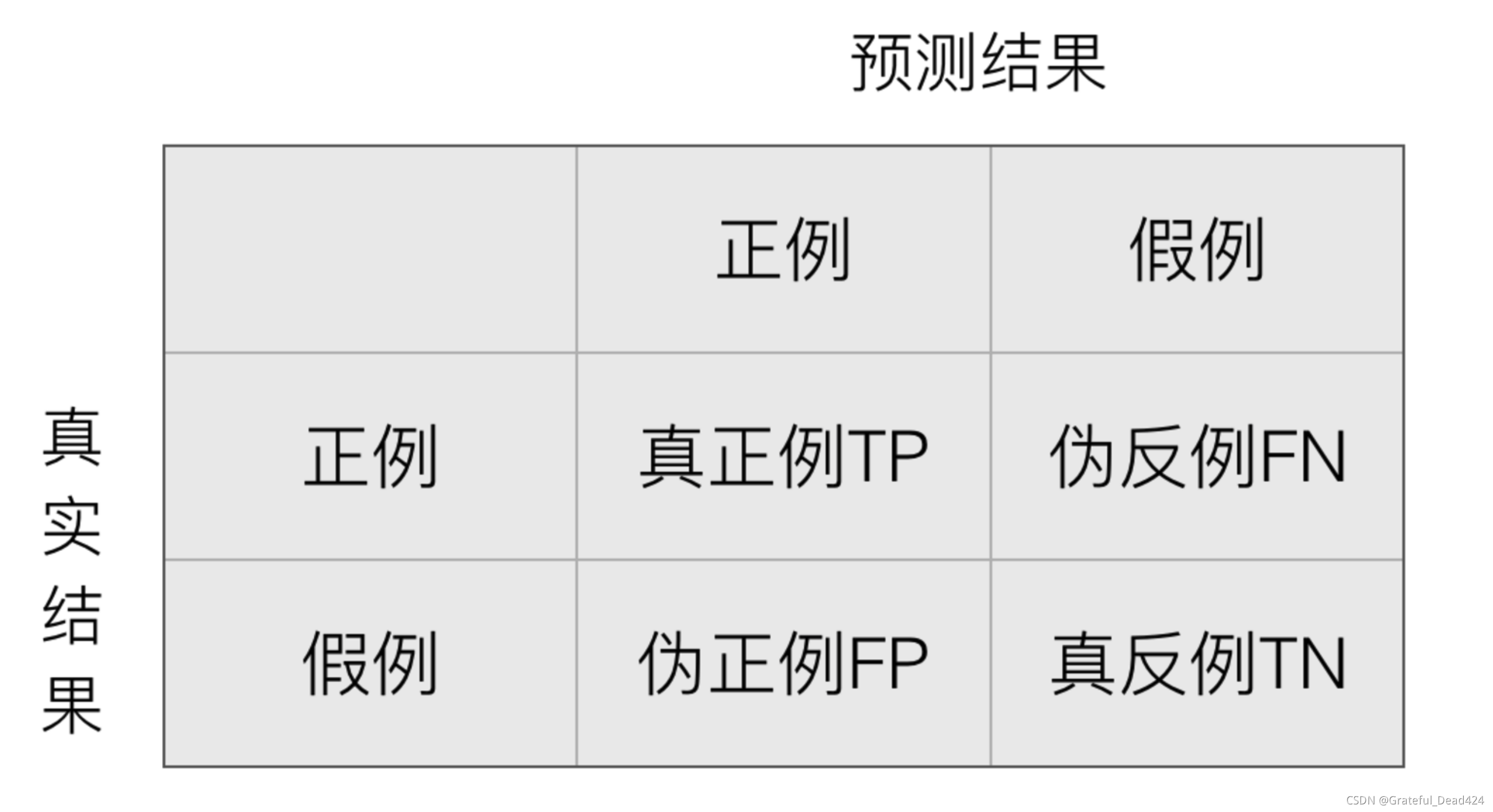
精确率(Precision)与召回率(Recall)

精确率：预测结果为正例样本中真实为正例的比例（查得准）

召回率：真实为正例的样本中预测结果为正例的比例（查的全，对正样本的区分能力）

其他分类标准，F1-score，反映了模型的稳健型??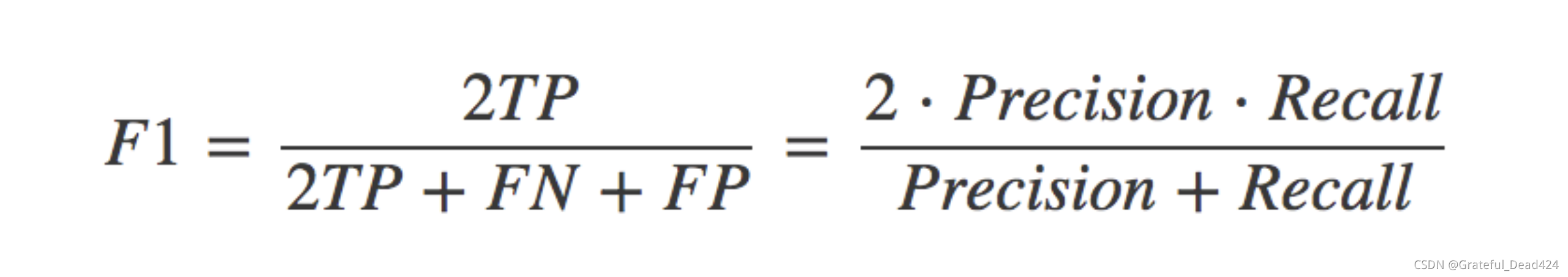

分类模型评估API?

sklearn.metrics.classification_report?

classification_report

sklearn.metrics.classification_report(y_true, y_pred, target_names=None)

1. y_true：真实目标值
2. y_pred：估计器预测目标值
3. target_names：目标类别名称
4. return：每个类别精确率与召回率

30.交叉验证与网格搜索对K-近邻算法调优

交叉验证与网格搜索

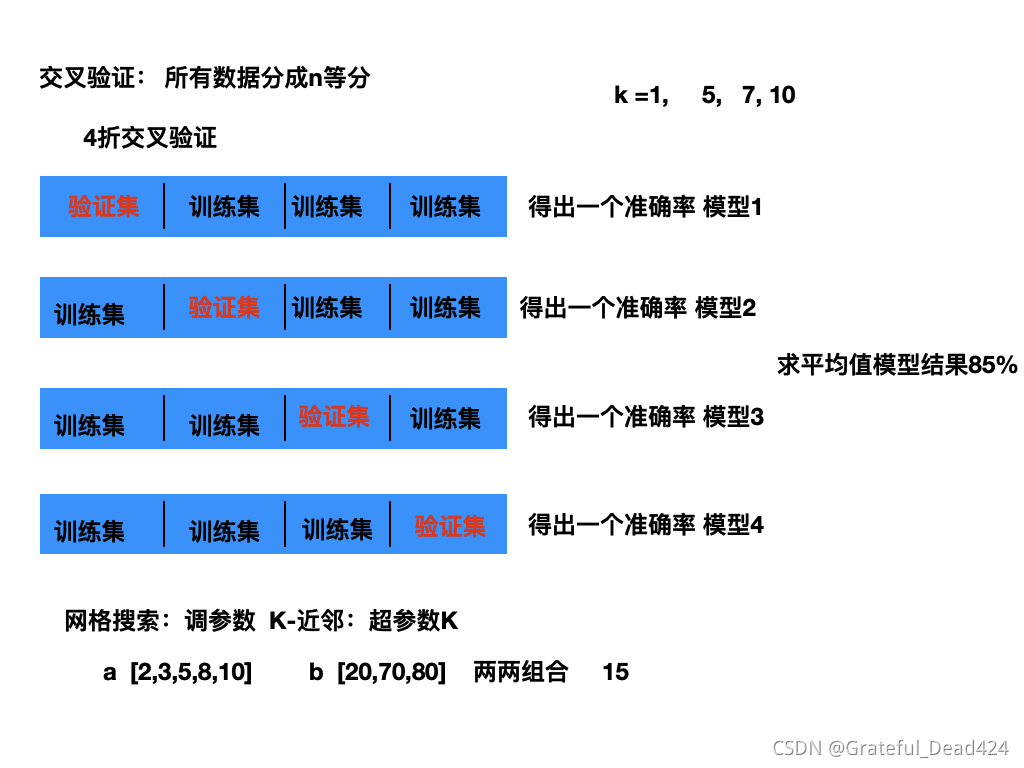
超参数搜索-网格搜索?

通常情况下，有很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。?

超参数搜索-网格搜索API

• sklearn.model_selection.GridSearchCV

GridSearchCV

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)

• 对估计器的指定参数值进行详尽搜索
• estimator：估计器对象
• param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
• cv：指定几折交叉验证
• fit：输入训练数据
• score：准确率 结果分析：
• best_score_:在交叉验证中测试的最好结果
• best_estimator_：最好的参数模型
• cv_results_:每次交叉验证后的测试集准确率结果和训练集准确率结果

from sklearn.neighbors import KNeighborsClassifier
import pandas as pd
from sklearn.model_selection import train_test_split,GridSearchCV
from sklearn.preprocessing import StandardScaler

def knncls():
    # 读取收据
    data = pd.read_csv("/Users/zhucan/Downloads/facebook-v-predicting-check-ins/train.csv")
    # 处理数据
    data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75")
    time_value = pd.to_datetime(data["time"], unit="s")
    # 把日期格式转换成字典格式
    time_value = pd.DatetimeIndex(time_value)
    # 构造一些特征
    data["day"] = time_value.day
    data["hour"] = time_value.hour
    data["weekday"] = time_value.weekday
    data = data.drop(["time"], axis=1)
    # 把签到数量少于n个目标位置删除
    place_count = data.groupby('place_id').count()
    tf = place_count[place_count.row_id > 3].reset_index()
    data = data[data['place_id'].isin(tf.place_id)]
    # 取出数据当中的特征值和目标值
    y = data["place_id"]
    x = data.drop(["place_id"], axis=1)

    # 进行数据的分割训练集和测试集
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)
    # 特征工程（标准化）
    std = StandardScaler()
    # 对特征值进行标准化
    x_train = std.fit_transform(x_train)
    x_test = std.transform(x_test)

    # 算法流程
    knn = KNeighborsClassifier()
    #构造一些参数的值进行搜索
    param = {"n_neighbors":[3,5,10]}
    # 进行网格搜寻
    gc = GridSearchCV(knn,param_grid=param,cv=2)
    gc.fit(x_train,y_train)

    #预测准确率
    print("在测试集上准确率:",gc.score(x_test,y_test))
    print("在交叉验证当中最好的结果:",gc.best_score_)
    print("选择最好的模型是:",gc.best_estimator_)
    print("每个超参数每次交叉验证的结果:",gc.cv_results_)
    return None

if __name__ == "__main__":
    knncls()

在测试集上准确率： 0.4867612293144208
在交叉验证当中最好的结果： 0.44459331651954603
选择最好的模型是： KNeighborsClassifier(n_neighbors=10)
每个超参数每次交叉验证的结果： {'mean_fit_time': array([0.00378036, 0.00375617, 0.00387752]), 'std_fit_time': array([0.00018954, 0.0001651 , 0.00021541]), 'mean_score_time': array([0.14799261, 0.1550293 , 0.18861997]), 'std_score_time': array([0.00120759, 0.00264049, 0.00127685]), 'param_n_neighbors': masked_array(data=[3, 5, 10],
             mask=[False, False, False],
       fill_value='?',
            dtype=object), 'params': [{'n_neighbors': 3}, {'n_neighbors': 5}, {'n_neighbors': 10}], 'split0_test_score': array([0.42701765, 0.44514502, 0.44813997]), 'split1_test_score': array([0.42354981, 0.43773644, 0.44104666]), 'mean_test_score': array([0.42528373, 0.44144073, 0.44459332]), 'std_test_score': array([0.00173392, 0.00370429, 0.00354666]), 'rank_test_score': array([3, 2, 1], dtype=int32)}