FC-GAGA: Fully Connected Gated Graph Architecture for Spatio-Temporal Traffic Forecasting
1.文章概述
本文提出了一种新的学习体系结构,它可以在不需要图的知识的情况下,获得与现有现存算法相当或更好的性能。该架构的关键要素是可学习的全连接硬图选通机制,该机制支持在交通预测应用中使用最先进且计算效率高的全连接时间序列预测架构。
图建模当前存在局限性:
-
这些模型的复杂性和运行时要高得多
-
些模型依赖于由领域专家提供的变量之间关系的定义
-
现有的模型往往依赖于马尔科夫假设,以使建模跨变量的相互作用易于处理
本文创新点:
本文提出了一种称为FC-GAGA的新架构,该架构将作者之前提出的全连接TS模型N-BEA (Oreshkin et al. 2020)和本文提出的硬图门机制的结合。为了生成单个TS(图形模型中的节点)的预测,它用可学习的图权值对所有其他节点的历史观测值进行加权,通过ReLU对它们进行配门,然后将所有节点的配门观测值叠加,通过全连通残差块对其进行处理。
- 不再依赖与图结构知识,使用一个非线性函数就可以学习到节点间的关系
- 如果将结构进行堆叠,每一层学习到的就是不同的图结构和图卷积一直使用同一个图存在差别
- 同时,FC-GAGA是内存和计算高效的结构
2. 问题陈述
| 变量 | 含义 |
|---|---|
| V V V | 节点 |
| E E E | 用于捕捉节点间关系 |
| y v = [ y v , 1 … , y y , T ] y_v=[y_{v,1}\ldots,y_{y,T}] yv?=[yv,1?…,yy,T?] | 输入观测值 |
3. FC-GAGN
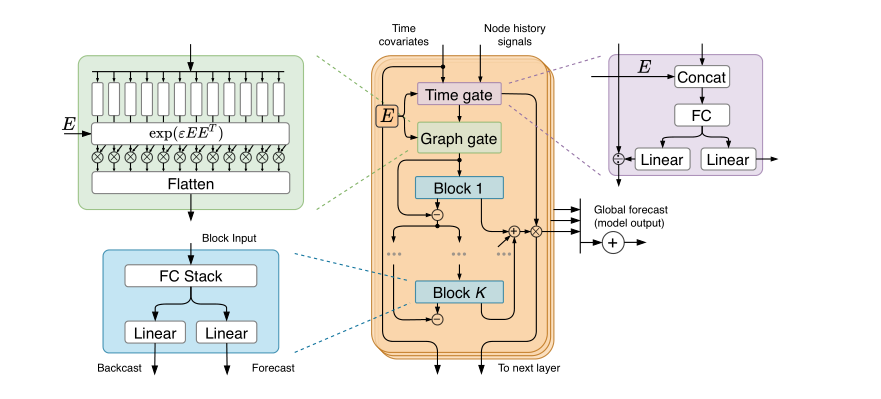
每个节点使用维度为 d d d的向量 e i = [ e i , 1 , … , e i , d ] e_i=[e_{i,1},\ldots,e_i,d] ei?=[ei,1?,…,ei?,d]表示,所有节点由节点嵌入矩阵 E E E表示
3.1 Graph edge weights
节点连接强度矩阵由节点嵌入矩阵获得:
W
=
e
x
p
(
ε
E
E
T
)
W=exp(\varepsilon EE^T)
W=exp(εEET)
3.2 Time gate block

时间门模块对时间time covariate features(例如,一天的时间,一周的时间等)进行建模,这些特征可能与节点观测一起可用。在FC-GAGA的每一层采用全连接层得到前向和后向的时间特性,在该层输入时除以后向时间特征,在输出预测时乘以前向时间特性。
此外为了捕捉不同节点的不同周期性特征,该模块的输入将节点嵌入E与每个节点时间特征向量进行凭借
3.3 Graph gate block
FC-GAGA的输入为
X
∈
R
N
×
w
X\in R^{N\times w}
X∈RN×w,为所有节点长度为
w
w
w的历史观测值,
x
i
~
=
m
a
x
j
X
i
,
j
\widetilde{x_i}=max_jX_{i,j}
xi?
?=maxj?Xi,j?,门控矩阵
G
∈
R
N
×
N
w
G\in R^{N\times Nw}
G∈RN×Nw
G
i
,
j
+
k
=
R
E
L
U
[
W
i
,
j
X
j
,
k
?
x
~
i
]
/
x
~
i
\boldsymbol{G}_{i, j+k}=R E L U\left[\boldsymbol{W}_{i, j} \boldsymbol{X}_{j, k}-\tilde{\boldsymbol{x}}_{i}\right] / \tilde{\boldsymbol{x}}_{i}
Gi,j+k?=RELU[Wi,j?Xj,k??x~i?]/x~i?
其中
W
i
,
j
W_{i,j}
Wi,j?是两个节点的连接权值,
X
j
,
k
X_{j,k}
Xj,k?是节点
j
j
j第
k
k
k个历史观察值,图的门控通过两个机制将节点i,j收集的信息关联起来:
- 节点i和j中的测量值通过RELU内部的减法和平滑操作相互关联
- RELU函数可以在不改变W的情况下关闭不相关点之间的连接
3.4 Fully connected time-series block
我们提出了一种全连通残差架构,该架构包含L个隐含层,R个残差块,并在节点间共享权值。其输入
Z
i
=
[
E
,
X
/
x
~
,
G
]
T
Z_i=[E,X /\tilde{x},G]^T
Zi?=[E,X/x~,G]T,其全连接层公式可以表示为:
F
C
r
,
?
(
H
r
,
?
?
1
)
≡
ReLU
?
(
A
r
,
?
H
r
,
?
?
1
+
b
r
,
?
)
\mathrm{FC}_{r, \ell}\left(\mathbf{H}^{r, \ell-1}\right) \equiv \operatorname{ReLU}\left(\mathbf{A}^{r, \ell} \mathbf{H}^{r, \ell-1}+\mathbf{b}^{r, \ell}\right)
FCr,??(Hr,??1)≡ReLU(Ar,?Hr,??1+br,?)
其中
A
r
,
l
A^{r,l}
Ar,l和
b
r
,
l
b^{r,l}
br,l分别表示第r个残差块中的第l层的权重和偏置。全连通残差TS建模体系结构的操作描述如下:
Z
r
=
ReLU
?
[
Z
r
?
1
?
Z
^
r
?
1
]
H
r
,
1
=
F
C
r
,
1
(
Z
r
)
,
…
,
H
r
,
L
=
F
C
r
,
L
(
H
r
,
L
?
1
)
Z
^
r
=
B
r
H
r
,
L
,
Y
^
r
=
(
H
r
,
L
)
T
F
r
\begin{aligned} \mathbf{Z}^{r} &=\operatorname{ReLU}\left[\mathbf{Z}^{r-1}-\widehat{\mathbf{Z}}^{r-1}\right] \\ \mathbf{H}^{r, 1} &=\mathrm{FC}_{r, 1}\left(\mathbf{Z}^{r}\right), \ldots, \mathbf{H}^{r, L}=\mathrm{FC}_{r, L}\left(\mathbf{H}^{r, L-1}\right) \\ \widehat{\mathbf{Z}}^{r} &=\mathbf{B}^{r} \mathbf{H}^{r, L}, \widehat{\mathbf{Y}}^{r}=\left(\mathbf{H}^{r, L}\right)^{T} \mathbf{F}^{r} \end{aligned}
ZrHr,1Z
r?=ReLU[Zr?1?Z
r?1]=FCr,1?(Zr),…,Hr,L=FCr,L?(Hr,L?1)=BrHr,L,Y
r=(Hr,L)TFr?
在每一个Layer会将每一个block进行累和,然后将于时间门控部分提取到的前向时间特征进行乘法操作,作为当前Layer的输出。
3.5 FC-GAGA layer stacking
FC-GAGA层的堆叠基于三个原则:
- 下一层接受前一层预测的总和作为输入
- 每个FC-GAGA层都有自己的一组节点嵌入,因此也有自己的图门
- 最终模型输出等于层预测的平均值
4. 实验
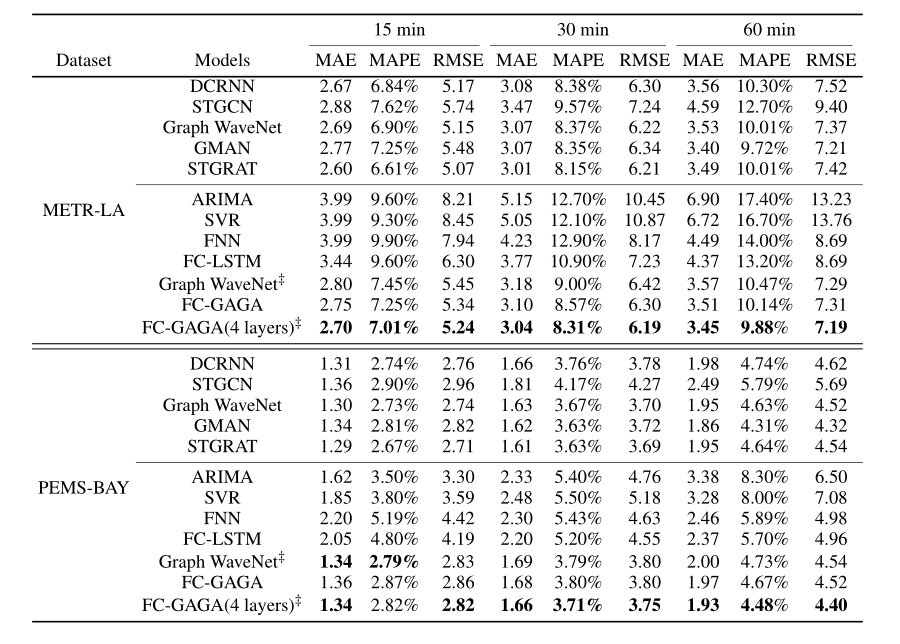
消融实验
- 层数的影响
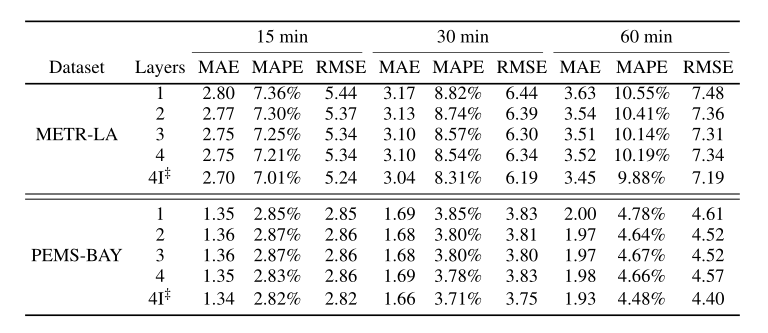
- 消融实验