文章目录
一、机器学习任务攻略
1.1 Framework of ML
神经网络一共包含三个模块:训练模块、验证模块、预测模块。其中训练和验证模块共用数据是Training data,但要注意的是要把Training data分成训练和验证数据。
训练步骤包括三个步骤:
1、要先写出一个有未知参数的函数f(x),x为input,也叫做feature
2、定义Loss函数,输入为一组参数,计算这组参数所造成的误差
3、定义optimization,找到一组最为合适的参数θ*,使得Loss最小
预测部分是用训练好的θ对Testing data进行预测结果。
1.2 提高结果的准确性
检查training data的Loss
1.2.1 Loss过大
显然在训练资料上效果并不是很好,这时要从两方面出发检查:
1.model bias的原因:
model过于简单,导致在神经网络的函数集中没有可以让Loss变的足够小的函数,就像在海中捞针
解决方法:重新设计model让其更加深,鲁棒性更强
1.增加输入的feature,或者使用Deep Learning


2.optimization做的不好
在训练过程中可能卡到一个局部最优点(local minima)的地方,虽然网络中存在一个最好的函数,但是你无法找到让Loss最小的一组参数θ*

如何区分是model bias还是optimization的问题
当一个神经网络的层数比另外一个神经网络要大,但Loss值却更大,则是optimization的问题,因为越深的网络的鲁棒性会更大;此外则是model bias的问题

1.2.2 Loss足够小,但testing data的Loss过大
这里也要从两方面分析
1.over fitting
举一个极端的例子:
我们的testing data为:
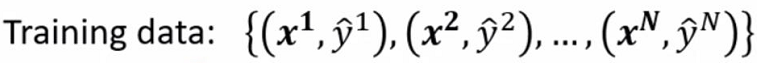
通过training找出这样一个函数:
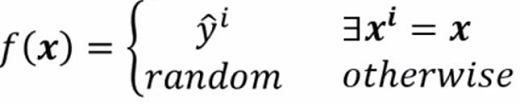
当能够在训练资料中找到x的话就输出yi,否则就随机输出一个值。基于此,这个函数在training过程中的Loss为0,但是在test过程中就什么也没干,所以在testing过程中的Loss会很大,这就是over fitting。
在真实的实验过程中,往往是因为model的鲁棒性太强,导致在training后得到的模型有很大的“自由区”而不能很好的拟合testing数据


导致Loss过大
解决方法:
1.增加数据量(Data augmentation)

2.限制model的鲁棒性
根据training的数据设定函数,少一些参数

但要注意的是不能给model太多的限制,否则会导致model bias的问题
综上,我们可以得出model的复杂程度和Loss的一个非线性关系

当model越来越复杂时,虽然Training loss越来越小,但是可能会出现over fitting的问题,导致预测结果不准
我们在前面说过,我们有三大模块,训练、验证和预测,且将training data随机分成训练数据和验证数据,当我们在每一个epoch训练后得到的θ参数和loss,我们要将θ进行验证,如果验证组得到的loss更小,说明这组参数是较优的,将此loss替换训练得到的loss,最终找到一组最优解
dev_mse = dev(model, dev_data)
if dev_mse < min_mse :
min_mse = dev_mse
def dev(model, dev_data) :
model.eval()
total_loss = []
for input, label in dev_data :
output = model(input)
total_loss.append(model.cal_loss(output, label))
return sum(total_loss) / len(total_loss)
此外我们还可以用N折交叉验证的方法进行分数据和找θ*

2.认为影响,这种问题不能怪model,机器是死的,这种问题一般来说叫做mismatch
二、局部最小值(local minima)与鞍点(saddle point)
当optimization失败时一般有两点原因:
1.loss值无法再小,此时已经找到了一组最优解θ*
2.gradient等于0
 这里我们对gradient==0的情况进行分析,当gradient等于0时,这个点有三种情况:
这里我们对gradient==0的情况进行分析,当gradient等于0时,这个点有三种情况:
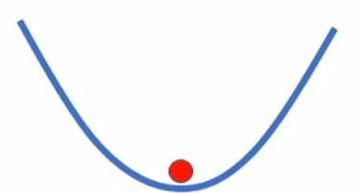
处于local minima,此时loss处于局部最小,没办法走到其他地方

值得注意的是,local minima也有好坏之分当minima处于尖端的时候,testing loss是十分大的,而在平缓区时,testing loss就没那么大

处于saddle point,此时loss并不是局部最小值,有别的地方可以走,这样就有机会到达全局最小点

Saddle Point vs Local Minima
他们两者之间谁更加常见呢?
如果在从二维空间去看的话Saddle Point就可能被认为是Local Minima
反过来假如我们从更高维度去看的话Local Minima却是Saddle Point

也就是说假如我们在某个维度没路可走的时候,我们可以提高维度来使其变成Saddle Point从而有路可走。这就是现在为什么神经网络如此复杂、参数众多的重要原因
三、Batch和momentum
3.1 Batch
现在假如说有一笔N资料,我们可以把N笔资料一次性全部跑完再计算loss和更新一次参数θ,但是的话我们也可以将N笔资料分成许多个batch资料,我们每跑完一个batch资料就计算更新一次参数

1 epoch等于把全部的batch都看一遍
为什么要用batch?
现在有20笔资料,我们分别看看用和不用batch的参数更新效果

可以看出没有用batch的model的蓄力时间比较长,但每走一步都比较稳;用了batch的model蓄力时间短,但每次走的时候方是十分乱的。但是如果考虑gpu的平行预算,没有用batch耗费的时间不一定比用了batch所花时间长。在MNIST机器学习任务(一共有六万笔资料)中:
跑每一个不同batch所用时间如下,(6000代表不用batch)

我们再看跑完一个epoch和跑完一个batch所需时间对比:

我们可以看出一个epoch大的batch花的时间反而是比较少的
但是与我们直觉不同的是,分了batch的任务最终预测的正确率是比没分batch是要高的

为什么分batch会带来更好的结果?
我们先来考虑Full batch的情况
我们沿着Loss函数来更新参数,当陷入一个local minima之后就停止更新参数

再考虑small batch时,当我们用θ1参数组来算gradient的时候,他的loss函数是L1当遇到gradient等于0时就卡住了,但不会停止更新函数,可以用下一个batch来train优化model

Small Batch VS Large Batch

正因他们有各自的优点,则Batch size变成一个hyper parameter(超参数)
3.2 Momentum
momentum是一门可能可以对抗local minima的技术。他的概念可以想象成物理世界中的惯性,我们可以想象,当一个小球沿着loss函数走,当走到local minima时因为他有惯性而不会在minima处停下

对于普通的gradient descent,假设开始在θ0的点,计算该点gradient为g(0),沿着gradient的反方向移动到θ1 = θ0 - ng(0) 然后计算g(1)…

结合momentum的gradient descent
我们在更新gradient时不单单沿着gradient的反方向,还要加上前一步(momentum)的方向进行更新,类似于物理中的力的合成,计算过程如下图:

当我们走到local minima和和saddle point时虽然gradient==0,但是由于我们还有前一步的momentum所以还会继续走下去

四、结语
以上是我机器学习学习笔记的第二篇,如有不对之处,还望指出,与君共勉。